Với giải Bài 27 trang 79 Toán lớp 9 chi tiết trong Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán lớp 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
Bài tập 27 trang 79 SGK Toán lớp 9 Tập 2: Cho đường tròn tâm O, đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh:
Lời giải:
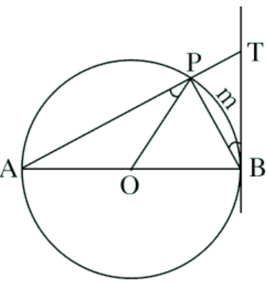
Xét đường tròn (O)
Có:
BT là tiếp tuyến của đường tròn (O) tại P
PB là dây cung
là góc tạo bởi tiếp tuyến và dây cung
sđ (1)
Mặt khác ta có: Góc PAO là góc nội tiếp đường tròn chắn cung PmB
sđ (2)
Từ (1) và (2) ta suy ra: (3)
Xét tam giác OAP có:
OA = OP (cùng bằng bán kính đường tròn tâm O)
Do đó, tam giác OAP cân tại O
(4) (tính chất tam giác cân)
Từ (3) và (4) ta suy ra: (đcpcm).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
