Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
Chứng minh rằng khi cát tuyến quay xung quang điểm thì có số đo không đổi.
Từ và vẽ hai tiếp tuyến với đường tròn. Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến quay xung quanh điểm
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải:
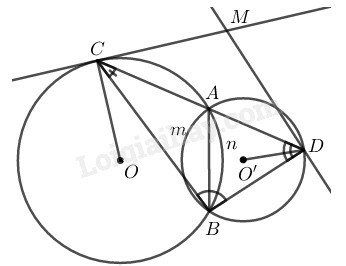
Ta có:
(góc nội tiếp trong đường tròn
(góc nội tiếp trong đường tròn
Vì điểm cố định nên không thay đổi
Vì vậy có số đo không đổi.
Ta có: không đổi do có số đo không đổi.
Vậy số đo luôn không đổi khi cát tuyến thay đổi .
Trong ta có
(hệ quả góc giữa tia tiếp tuyến và dây cung)
Trong ta có: (hệ quả góc giữa tia tiếp tuyến và dây cung)
Từ và suy ra:
Hay (không đổi do câu a)
Trong ta có:
Nên không đổi do không đổi.
Vậy không đổi.
Chứng minh rằng ta luôn có và tích này không phụ thuộc vị trí của cát tuyến
Ở hình khi cho tính bán kính đường tròn.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+) Hai tam giác đồng dạng thì ta có các cạnh tương ứng tỉ lệ.
Lời giải:
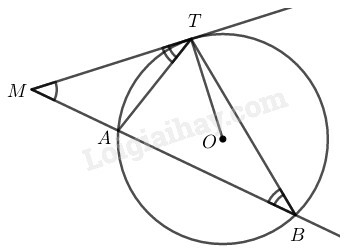
Xét và có:
+) chung
+) (hệ quả góc giữa tia tiếp tuyến và dây), hay
Suy ra: đồng dạng
Vì mà là tiếp tuyến của đường tròn nên tích không phụ thuộc vị trí của cát tuyến
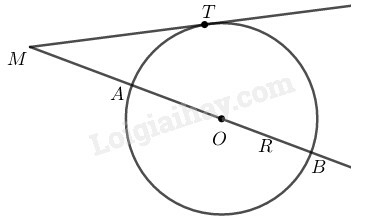
Gọi bán kính là
(chứng minh trên)
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+) Hai tam giác đồng dạng thì ta có các cạnh tương ứng tỉ lệ.
Lời giải:
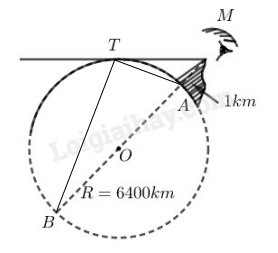
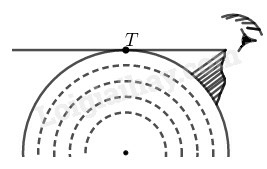
Điểm nhìn tối đa là tiếp tuyến kể từ mắt nhìn đến tiếp điểm của bề mặt trái đất (như hình vẽ)
Xét và có:
+) chung
+) (hệ quả góc giữa tia tiếp tuyến và dây)
Suy ra: đồng dạng
là chiều cao của đỉnh núi là
Thay số ta có:
(km)
Ta sử dụng kiến thức:
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+) Nếu các tia và thuộc cùng một nửa mặt phẳng có bờ chứa tia và thì tia và trùng nhau.
Lời giải:
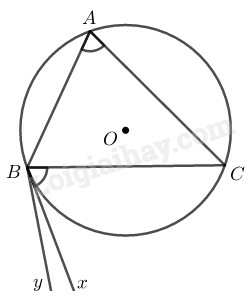
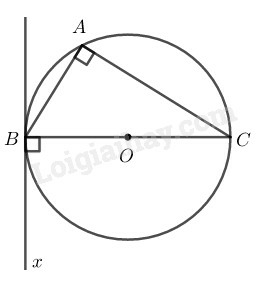
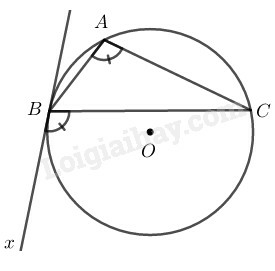
nội tiếp trong đường tròn có ba khả năng xảy ra của tam giác
- là tam giác nhọn
- là tam giác vuông
- là tam giác tù
Xét là tam giác nhọn (tam giác vuông và tam giác tù chứng minh tương tự)
Trên cùng nửa mặt phẳng bờ đường thẳng chứa tia ta kẻ tia là tiếp tuyến của đường tròn
(hệ quả của góc giữa tia tiếp tuyến và dây cung)
Mà
Suy ra:
Lại có và nằm trên cùng một nửa mặt phẳng bờ tạo với một góc bằng nhau.
Do đó, và trùng nhau.
Vậy là tiếp tuyến của đường tròn
Bài tập bổ sung (trang 104 SBT Toán 9)
Sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Nếu một đường thẳng cùng vuông góc với hai đường thẳng thì hai đường thẳng đó song song với nhau.
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+) Nếu một đường thẳng cắt hai đường thẳng song song thì tạo ra các cặp góc so le trong bằng nhau.
+) Tổng các góc trong một tứ giác bằng
Lời giải:
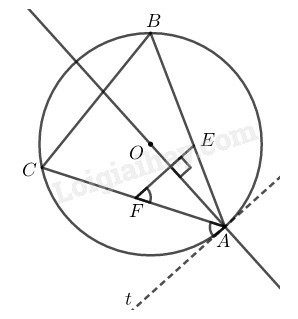
Kẻ tiếp tuyến của đường tròn
Suy ra: (tính chất tiếp tuyến)
Mà
Do đó:
Nên (so le trong)
Lại có: (hệ quả góc giữa tia tiếp tuyến và dây cung)
Suy ra: hay
Mà (hai góc kề bù)
Nên
Trong tứ giác ta có:
(tổng các góc trong tứ giác)
Từ và suy ra:
Ta sử dụng kiến thức:
+) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Trong tam giác cân, hai góc ở đáy bằng nhau.
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải:
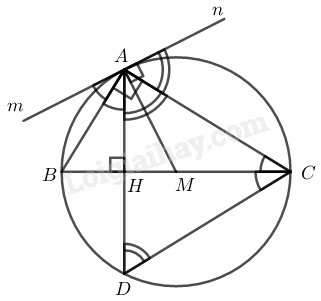
Vì vuông tại có là đường trung tuyến ứng với cạnh huyền
(tính chất tam giác vuông)
Nên đường tròn tâm bán kính đi qua
Gọi là giao điểm của với đường tròn
Khi đó: tại H nên H là trung điểm của AD (quan hệ giữa đường kính và dây của đường tròn)
là trung trực của
(tính chất đường trung trực của đoạn thẳng)
cân tại
Ta lại có: (hệ quả của góc giữa tia tiếp tuyến và dây cung)
Từ suy ra hay
Vậy là tia phân giác của
Ta có: (hệ quả của góc giữa tia tiếp tuyến và dây cung)
(cùng phụ với góc )
Từ suy ra .
Vậy là tia phân giác của .