Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 7: Hình bình hành hay, chi tiết giúp học sinh dễ dàng làm bài tập Hình bình hành lớp 8.

Giải bài tập Toán lớp 8 Bài 7: Hình bình hành

Trả lời câu hỏi giữa bài

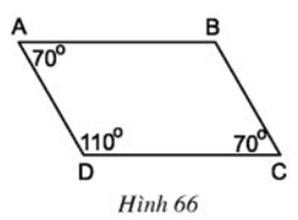
Câu hỏi 1 trang 90 Toán 8 Tập 1: Các cạnh đối của tứ giác ABCD trên hình 66 có gì đặc biệt?

Lời giải

Ta sử dụng thước thẳng đo các cặp cạnh đối AB và CD; AD và BC ta thấy các cặp cạnh này song song và bằng nhau.

Như vậy các cạnh đối của tứ giác ABCD song song và bằng nhau.

(Nhận xét trang 70: Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau).

Câu hỏi 2 trang 90 Toán 8 Tập 1: Cho hình bình hành ABCD (h.67). Hãy thử phát hiện tính chất về cạnh, về góc, về đường chéo của hình bình hành đó.

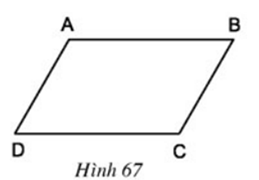
Lời giải

Sau khi quan sát, ta dự đoán hình bình hành ABCD có các tính chất sau:

- Các cạnh đối bằng nhau

- Các góc đối bằng nhau

- Hai đường chéo cắt nhau tại trung điểm mỗi đường.

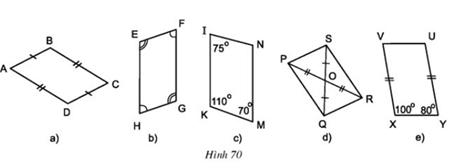
Câu hỏi 3 trang 92 Toán 8 Tập 1: Trong các tứ giác ở hình 70, tứ giác nào là hình bình hành? Vì sao?

Lời giải

Hình 70a):

Xét tứ giác ABCD, có:

AB = DC

AD = BC

Suy ra tứ giác ABCD là hình bình hình (các cạnh đối bằng nhau).

Hình 70b):

Xét tứ giác EFGH, có:

$$\begin{gathered} \widehat{E}=\widehat{G} \\ \widehat{H}=\widehat{F} \end{gathered}$$

Suy ra EFGH là hình bình hành (các góc đối bằng nhau).

Hình 70c):

Xét tứ giác MNIK, có:

$\widehat{K}+\widehat{M}={110}^0+{70}^0={180}^0\Rightarrow$MN//IK (hai góc trong cùng phía bù nhau)

$\widehat{K}+\widehat{I}={110}^0+{75}^0={185}^0\Rightarrow$IN và KM không song song

Suy ra MNIK là hình thang không phải hình bình hành.

Hình 70d):

Xét tứ giác PQRS, có:

Hai đường chéo cắt nhau tại trung điểm mỗi đường nên tứ giác PQRS là hình bình hành.

Hình 70e):

Xét tứ giác XYUV, có:

$\widehat{X}+\widehat{Y}={100}^0+{80}^0={180}^0$

Mà hai góc ở vị trí trong cùng phía nên XY // UV

Mặt khác XY = UV

Nên tứ giác XYUV là hình bình hành.

Bài tập (trang 92, 93)

Bài 43 trang 92 Toán 8 Tập 1: Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không?

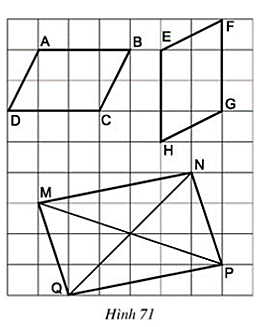
Lời giải: 

Xét tứ giác ABCD, có:

AB = CD ( = 3 ô)

AB // CD

Suy ra tứ giác ABCD là hình bình hành.

Xét tứ giác EFGH, có:

EH // FG

EH = FG (= 3 ô)

Suy ra tứ giác EFGH là hình bình hành

Xét tứ giác MNPQ có:

MN = PQ

MQ = NP

Suy ra tứ giác MNPQ là hình bình hành

Bài 44 trang 92 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF

Lời giải:

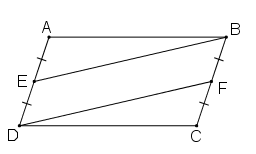
Cách 1: Sử dụng phương pháp chứng minh hai tam giác bằng nhau:

Vì ABCD là hình bình hành nên:

AB = CD (hai cạnh đối bằng nhau)

$\widehat{A}=\widehat{C}$(hai góc đối bằng nhau)

AD = BC $\Rightarrow$ AE = ED = BF = CF (E là trung điểm của AD, F là trung điểm của BC).

Xét $\Delta ABE$ và $\Delta CDF$, có:

AB = CD (cmt)

$\widehat{A}=\widehat{C}$ (cmt)

AE = CF (cmt)

⇒ ΔAEB = ΔCFD (c.g.c)

⇒ EB = DF (hai cạnh tương ứng).

Cách 2: Sử dụng phương pháp chứng minh tứ giác BEDF là hình bình hành

Vì ABCD là hình bình hành

⇒ AD//BC hay DE // BF và AD = BC.

Ta có: E là trung điểm của AD ⇒$DE=\frac{AB}{2}$

F là trung điểm của BC ⇒$BF=\frac{BC}{2}$

Mà AD = BC

⇒ DE = BF.

Xét tứ giác BEDF có:

DE // BF và DE = BF

⇒ BEDF là hình bình hành

⇒ BE = DF.

Bài 45 trang 92 Toán 8 Tập 1: Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF

b) Tứ giác DEBF là hình gì? Vì sao?

Lời giải

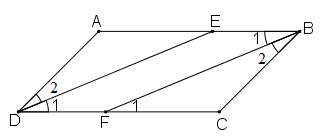
a) Ta có: $\widehat{D_1}=\widehat{D_2}=\frac{1}{2}\widehat{ADC}$ (DE là phân giác của $\widehat{ADC}$)

Ta lại có: $\widehat{B_1}=\widehat{B_2}=\frac{1}{2}\widehat{ABC}$(BF là phân giác của $\widehat{ABC}$)

Mà $\widehat{ADC}=\widehat{ABC}$ (ABCD là hình bình hành)

$\Rightarrow \widehat{D_1}=\widehat{B_1}$(1)

Vì ABCD là hình bình hành ⇒ AB // CD ⇒ $\widehat{B_1}=\widehat{F_1}$ (Hai góc so le trong) (2)

Từ (1) và (2) suy ra: $\Rightarrow \widehat{D_1}=\widehat{F_1}$

Mà hai góc này ở vị trí đồng vị

⇒ DE // BF (đpcm)

b) Xét tứ giác DEBF có:

DE // BF (chứng minh ở câu a)

BE // DF (vì AB // CD)

⇒ DEBF là hình bình hành.

Bài 46 trang 92 Toán 8 Tập 1:Các câu sau đúng hay sai?

a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành

b) Hình thang có hai cạnh bên song song là hình bình hành

c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành

d) Hình thang có hai cạnh bên bằng nhau là hình bình hành

Lời giải

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 5

b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

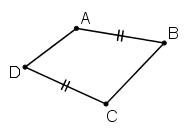
c) Sai.

Ví dụ tứ giác ABCD ở dưới có AB = CD nhưng không phải hình bình hành.

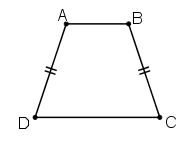
d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

Bài 47 trang 93 Toán 8 Tập 1: Cho hình 72. Trong đó ABCD là hình bình hành

a) Chứng minh rằng AHCK là hình bình hành

b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.

Lời giải

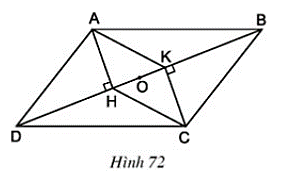
a) Vì ABCD là hình bình hành

⇒ AD // BC và AD = BC.

$\Rightarrow \widehat{ADH}=\widehat{ABK}$(hai góc so le trong)

Xét $\Delta AHD$ và $\Delta CKB$, có:

$\widehat{AHD}=\widehat{CKB}={90}^0$

AD = BC (cmt)

$\widehat{ADH}=\widehat{ABK}$(cmt)

⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn)

⇒ AH = CK

Ta có: AH ⊥ BD; CK ⊥ BD ⇒ AH // CK

Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.

b) Hình bình hành AHCK có O là trung điểm HK nên O là trung điểm của AC

⇒ A, C, O thẳng hàng.

Bài 48 trang 93 Toán 8 Tập 1: Tứ giác ABCD có E, F , G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Lời giải:

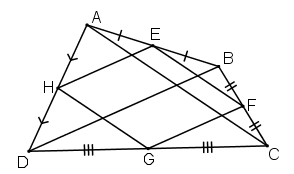
+) Xét có:

E là trung điểm AB

F là trung điểm BC

⇒ EF là đường trung bình của tam giác ABC

⇒ EF // AC và $\text{EF}=\frac{AC}{2}$ (1)

+) Xét $\Delta ADC$, có:

H là trung điểm AD

G là trung điểm CD

⇒ HG là đường trung bình của tam giác ACD

⇒ HG // AC và $HG=\frac{AC}{2}$ (2)

Từ (1) và (2) suy ra : EF // HG (cùng // AC) và EF = HG (cùng bằng AC)

⇒ tứ giác EFGH là hình bình hành.

Bài 49 trang 93 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:

a) AI // CK

b) DM = MN = NB

Lời giải:

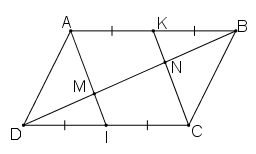
a) Ta có: K là trung điểm của AB $\Rightarrow AK=\frac{AC}{2}$.

Ta có: I là trung điểm của CD $\Rightarrow CI=\frac{CD}{2}$.

Vì ABCD là hình bình hành

⇒ AB // CD hay AK // CI

và AB = CD hay AK = CI

Xét tứ giác AKCI có AK // CI và AK = CI

⇒ AKCI là hình bình hành.

b) Vì AKCI là hình bình hành

⇒ AI//KC hay MI//NC.

Xét ΔDNC có:

I là trung điểm DC

IM // NC

⇒ M là trung điểm DN

⇒ DM = MN (1)

Xét ΔBAM có:

K là trung điểm AB

KN//AM

⇒ N là trung điểm BM

⇒ MN = NB (2)

Từ (1) và (2) suy ra DM = MN = NB.