Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 1 Bài 7: Hình bình hành. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 7:Hình bình hành. Mời các bạn đón xem:

Bài tập Toán 8 Chương 1 Bài 7: Hình bình hành

A. Bài tập Hình bình hành

I. Bài tập trắc nghiệm

Bài 1: Chọn phương án sai trong các phương án sau?

A. Tứ giác có các cạnh đối song song là hình bình hành.

B. Tứ giác có các cạnh đối bằng nhau là hình bình hành.

C. Tứ giác có hai góc đối bằng nhau là hình bình hành.

D. Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

Lời giải:

Dấu hiệu nhận biết hình bình hành.

+ Tứ giác có các cạnh đối song song là hình bình hành.

+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

+ Tứ giác có các góc đối bằng nhau là hình bình hành.

+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

→ Đáp án C sai.

Chọn đáp án C.

Bài 2: Chọn phương án đúng trong các phương án sau.

A. Hình bình hành là tứ giác có hai cạnh đối song song.

B. Hình bình hành là tứ giác có các góc bằng nhau.

C. Hình bình hành là tứ giác có các cạnh đối song song.

D. Hình bình hành là hình thang có hai cạnh kề bằng nhau.

Lời giải:

Trong tính chất của hình bình hành:

Định lí: Trong hình bình hành:

+ Các cạnh đối bằng nhau.

+ Các góc đối bằng nhau.

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

→ Đáp án C đúng.

Chọn đáp án C.

Bài 3: Cho hình bình hành ABCD có $\hat{A}$ = 120⁰, các góc còn lại của hình bình hành là?

   A. $\hat{B}$ˆ = 60⁰, $\hat{C}$ˆ = 120⁰, $\hat{D}$ˆ = 60⁰.

   B. $\hat{B}$ˆ = 110⁰, $\hat{C}$ˆ = 80⁰, $\hat{D}$ˆ = 60⁰.

   C. $\hat{B}$ˆ = 80⁰, $\hat{C}$ˆ = 120⁰, $\hat{D}$ = 80⁰.

   D. $\hat{B}$ˆ = 120⁰, $\hat{C}$ˆ = 60⁰, $\hat{D}$ˆ = 120⁰.

Lời giải:

Trong tính chất của hình bình hành:

Định lí: Trong hình bình hành:

+ Các cạnh đối bằng nhau.

+ Các góc đối bằng nhau.

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường

⇒ $\hat{A}=\hat{C}$ˆ = 120⁰.

Khi đó ta có: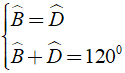 ⇒ $\hat{B}=\hat{D}$ˆ = 60⁰

Chọn đáp án A.

Bài 4: Cho hình bình hành ABCD có $\hat{A}-\hat{B}$ = 20⁰. Xác định số đo góc A và B?

A. $\hat{A}$= 80⁰, $\hat{B}$ˆ = 100⁰

B. $\hat{A}$ˆ = 100⁰ˆ , $\hat{B}$= 80⁰

C. $\hat{A}$ = 80⁰, $\hat{B}$ˆ = 60⁰

D. $\hat{A}$ˆ = 120⁰, $\hat{B}$ˆ = 100⁰

Lời giải:

Theo giả thiết, ta có: $\hat{A}-\hat{B}$ˆ = 20⁰ ⇒ $\hat{A}=\hat{B}$ˆ + 20⁰

Mặt khác ABCD là hình bình hành nên $\hat{A}+\hat{B}$ˆ = 180⁰

Khi đó: 

Chọn đáp án B.

Bài 5: Cho hình bình hành ABCD, có I là giao điểm của AC và BD. Chọn phương án đúng trong các phương án sau

A. AC = BD

B. Δ ABD cân tại A.

C. BI là đường trung tuyến của Δ ABC

D. $\hat{A}+\hat{C}=\hat{B}+\hat{D}$

Lời giải:

Trong hình bình hành các góc đối bằng nhau

Hay 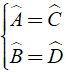 ⇒ $\hat{A}+\hat{B}=\hat{C}+\hat{D}$ˆ → đáp án D sai.

+ Δ ABD cân tại A khi và chỉ khi AB = AD nhưng theo giả thiết ta chưa có dữ kiện này

→ Đáp án B sai.

+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

→ Đáp án A sai vì theo giả thiết chưa đủ dữ kiện

Chọn đáp án C.

Bài 6: Cho tam giác ABC có M, N và P lần lượt là trung điểm AB, AC và BC. Tìm khẳng định sai ?

A. Tứ giác AMNP là hình bình hành.

B. MP // AC

C. MN = $\frac{BC}{2}$

D. Tứ giác MNCP là hình bình hành.

Lời giải:

* Ta có M và N lần lượt là trung điểm của AB và AC

Suy ra: MN là đường trung bình của tam giác ABC.

⇒ MN // BC

* Vì M và P lần lượt là trung điểm của AB và BC nên MP là đường trung bình của tam giác ABC.

⇒ MP // AC

* Tứ giác MNCP có cạnh đối song song với nhau nên tứ giác MNCP là hình bình hành.

Chọn đáp án A

Bài 7: Cho hình thang ABCD có AD// BC và $\widehat{BAD}$ = 100^o; $\widehat{ADC}$ = 80^o. Tìm khẳng định sai

A. AB = CD; AD = BC

B. Tứ giác ABCD là hình bình hành

C. 

D. AC = BD

Lời giải:

* Ta có: 

Và 2 góc này ở vị trí trong cùng phía nên AB// CD (1)

* Lại có: AD// BC ( giả thiết) (2)

Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành (dấu hiệu nhận biết).

* Suy ra: AB = CD; AD = BC;

Chọn đáp án D

Bài 8: Cho hình bình hành ABCD, gọi E và F là trung điểm của AD và BC. Gọi I là giao điểm của AC và BD. Tìm khẳng định sai?

A. Tứ giác ABFE là hình bình hành

B. EI là đường trung bình của tam giác ACD

C. AI = ID

D. Tứ giác EFCD là hình bình hành

Lời giải:

* Ta có ABCD là hình bình hành nên AB = CD; ABCD đồng thời là hình thang có 2 đáy là AB và CD.

Vì E và F lần lượt là trung điểm của AD và BC nên EF là đường trung bình của hình thang ABCD

Suy ra: EF// AB// CD và

(vì AB = CD)

* Xét tứ giác ABFE có AB// EF và AE// BF nên ABFE là hình bình hành

Tương tự, tứ giác EFCD là hình bình hành.

* Theo tính chất hình bình hành ta có: I là trung điểm của AC và BD.

Tam giác ACD có E và I lần lượt là trung điểm của AD và AC nên EI là đường trung bình của tam giác

Chọn đáp án C

Bài 9: Cho hình bình hành ABCD có 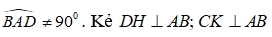 Tìm khẳng định sai?

A. Tứ giác HKCD là hình bình hành.

B. AC = DK

C. ΔDHA = ΔCKB

D. HA = KB

Lời giải:

* Ta có: 

nên DH // CK.

Vì ABCD là hình bình hành nên AB // CD hay HK// CD.

Xét tứ giác HKCD có: DH// CK và HK// CD nên tứ giác HKCD là hình bình hành.

* Xét ΔDHA và ΔCKB có:

DH = CK (vì HKCD là hình bình hành)

AD = BC (vì ABCD là hình bình hành)

Suy ra: ΔDHA = ΔCKB (c.g.c)

Suy ra: HA = KB (2 cạnh tương ứng)

Chọn đáp án B

Bài 10: Cho tứ giác ABCD có: $\hat{A}$ = 100^o, $\hat{D}$ = 80^o và AB = CD. Tìm khẳng định sai?

A. AC = BD

B. Tứ giác ABCD là hình bình hành

C. AD = BC

D. $\hat{B}$ = 80^o, $\hat{C}$ = 100^o

Lời giải:

* Ta có: $\hat{A}$ + $\hat{D}$ = 180^o mà hai góc này ở vị trí trong cùng phía nên: AB // CD

* Lại có: AB = CD ( giả thiết)

Suy ra: Tứ giác ABCD là hình bình hành ( dấu hiệu nhận biết)

* Suy ra: AD = BC và $\hat{B}$ = $\hat{D}$ = 80^o, $\hat{A}=\hat{C}$= 100^o

Chọn đáp án A

Bài 11: Cho hình bình hành ABCD có 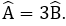 Số đo các góc của hình bình hành là:

Lời giải:

Đáp án cần chọn là: B

Bài 12: Tính số đo các góc của hình bình hành ABCD biết 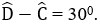 Ta được:

Lời giải:

Theo định lí tổng số các góc trong tứ giác ta có:

Đáp án cần chọn là: B

Bài 13: Tính số đo các góc của hình bình hành ABCD biết 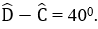 Ta đươc:

Lời giải:

Theo định lí tổng số các góc trong tứ giác ta có:

Đáp án cần chọn là: B

Bài 14: Hãy chọn câu trả lời sai.

Cho hình vẽ, ta có:

A. ABCD là hình bình hành  

B. AB // CD

C. ABCE là hình thang cân   

D. BC // AD

Lời giải:

Từ hình vẽ ta có O là trung điểm của BD và AC. Do đó tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm mỗi đường, suy ra tứ giác ABCD là hình bình hành ⇒ A đúng

Vì ABCD là hình bình hành nên AB // CD; AD // BC (tính chất) ⇒ B, D đúng.

Chưa đủ điều điều kiện để ABCE là hình thang cân

Đáp án cần chọn là: C

Bài 15: Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD tại M. Tia phân giác góc C cắt AB tại N (hình vẽ). Hãy chọn câu trả lời sai.

A. AMCN là hình bình hành             

B. CMBA là hình thang

C. ANCD là hình thang cân               

D. AN = MC

Lời giải:

Mà hai góc  ở vị trí đồng vị nên AM // CN.

Do AB // CD (gt), N Є AB, M Є BC ⇒ AN // MC.

Tứ giác AMCN có AN // CM, AM // CN (cmt) nên là hình bình hành (dấu hiệu nhận biết).

Vì AMCN là hình bình hành nên AN = CM (tính chất) nên A, D đúng.

Bì MC // AB ⇒ AMCB là hình thang nên B đúng.

Vì AN // CD ⇒ ANCD là hình thang

Chưa đủ điều kiện để ANCD là hình thang cân nên C sai.

Đáp án cần chọn là: C

II. Bài tập tự luận có lời giải

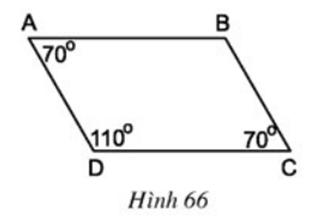
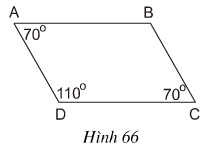
Bài 1: Các cạnh đối của tứ giác ABCD trên hình 66 có gì đặc biệt?

Lời giải

Các cạnh đối của tứ giác ABCD bằng nhau và song song với nhau

(Nhận xét trang 70: Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau)

Bài 2 Cho hình bình hành ABCD (h.67). Hãy thử phát hiện tính chất về cạnh, về góc, về đường chéo của hình bình hành đó.

Lời giải

- Các cạnh đối bằng nhau

- Các góc đối bằng nhau

- Hai đường chéo cắt nhau tại trung điểm mỗi đường

Bài 3 Trong các tứ giác ở hình 70, tứ giác nào là hình bình hành? Vì sao?

Lời giải

ABCD là hình bình hình vì có các cạnh đối bằng nhau

EFGH là hình bình hành vì có các góc đối bằng nhau

PQRS là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường

XYUV là hình bình hành vì có XV = YU và XV // YU

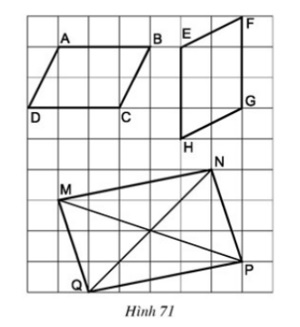
Bài 4 Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không?

Lời giải:

Cả ba tứ giác là hình bình hành

- Tứ giác ABCD là hình bình hành vì có AB // CD và AB = CD = 3 (dấu hiệu nhận biết 3)

- Tứ giác EFGH là hình bình hành vì có EH // FG và EH = FH = 3 (dấu hiệu nhận biết 3)

- Tứ giác MNPQ là hình bình hành vì có MN = PQ và MQ = NP (dấu hiệu nhận biết 2)

(Chú ý:

- Với các tứ giác ABCD, EFGH còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 2.

- Với tứ giác MNPQ còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 5.)

Bài 5 Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF

Lời giải:

Ta có:

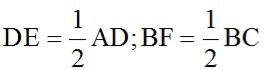
Mà AD = BF (ABCD là hình bình hành)

=> DE = BF

Tứ giác BEDF có:

DE // BF (vì AD // BC)

DE = BF

Nên BEDF là hình bình hành suy ra BE = DF

Bài 6 Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF

b) Tứ giác DEBF là hình gì? Vì sao?

Lời giải:

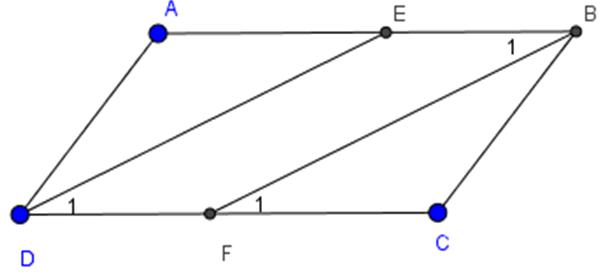
a) Ta có:

+ ABCD là hình bình hành ⇒ AB // CD ⇒  (Hai góc so le trong) (1)

+ DE là tia phân giác của góc D

Mà hai góc này ở vị trí đồng vị ⇒ DE // BF (đpcm)

b) Tứ giác DEBF có:

DE // BF (chứng minh ở câu a)

BE // DF (vì AB // CD)

Nên theo định nghĩa DEBF là hình bình hành.

Bài 7 Các câu sau đúng hay sai?

a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành

b) Hình thang có hai cạnh bên song song là hình bình hành

c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành

d) Hình thang có hai cạnh bên bằng nhau là hình bình hành

Lời giải:

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 5

b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

c) Sai, vì hình thang cân có hai cạnh đối (hai cạnh bên) bằng nhau nhưng nó không phải là hình bình hành

d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

Bài 8 Cho hình 72. Trong đó ABCD là hình bình hành

a) Chứng minh rằng AHCK là hình bình hành

b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.

Lời giải:

a)+ ABCD là hình bình hành

⇒ AD // BC và AD = BC.

⇒ $\widehat{ADH}=\widehat{CBK}$ (Hai góc so le trong).

Hai tam giác vuông AHD và CKB có:

    AD = BC

    $\widehat{ADH}=\widehat{CKB}$

⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn)

⇒ AH = CK

+ AH ⊥ BD; CK ⊥ BD ⇒ AH // CK

Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.

b) Xét hình bình hành AHCK, trung điểm O của đường chéo HK cũng là trung điểm của đường chéo AC (tính chất đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng

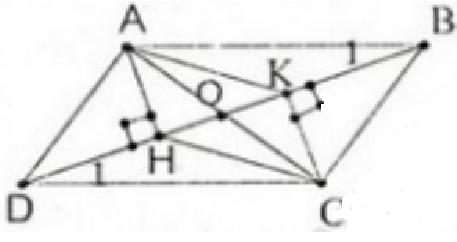
Bài 9 Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Lời giải:

Tứ giác EFGH là hình bình hành

- Cách 1:

EB = EA, FB = FC (gt) nên EF là đường trung bình của ΔABC

Do đó EF // AC.

Tương tự HG là đường trung bình của ΔACD do đó HG // AC

Suy ra EF // HG (1)

Tương tự: EH // FG (2)

Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiệu nhận biết 1).

- Cách 2:

Suy ra EF = HG.

Lại có EF // HG (cmt)

Vậy EFGH là hình bình hành (dấu hiệu nhận biết 3)

Bài 10 Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:

a) AI // CK

b) DM = MN = NB

Lời giải:

a) + K là trung điểm của AB ⇒ AK = $\frac{AB}{2}$

+ I là trung điểm của CD ⇒ CI = $\frac{CD}{2}$.

+ ABCD là hình bình hành

⇒ AB // CD hay AK // CI

và AB = CD ⇒ $\frac{AB}{2}=\frac{CD}{2}$ hay AK = CI

+ Tứ giác AKCI có AK // CI và AK = CI

⇒ AKCI là hình bình hành.

b) + AKCI là hình bình hành

⇒ AI//KC hay MI//NC.

ΔDNC có: DI = IC, IM // NC ⇒ DM = MN (1)

+ AI // KC hay KN//AM

ΔBAM có: AK = KB, KN//AM ⇒ MN = NB (2)

Từ (1) và (2) suy ra DM = MN = NB.

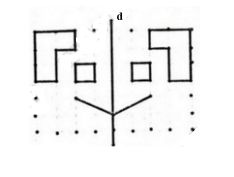
Bài 11 Vẽ hình đối xứng với các hình đã cho qua trục d (h.58).

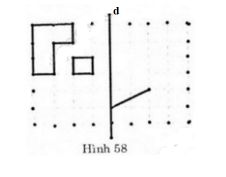
Lời giải:

Vẽ hình:

Bài 12 Cho góc xOy có số đo 50^o, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.

a) So sánh các độ dài OB và OC

b) Tính số đo góc BOC

Lời giải:

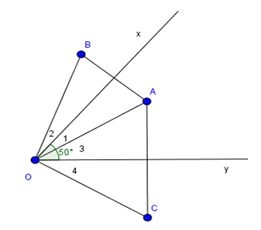
a) Ox là đường trung trực của AB suy ra OA = OB

Oy là đường trung trực của AC suy ra OA = OC

=> OB = OC

b) ΔAOB cân tại O (vì OA = OB)

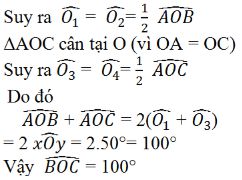
Bài 13 Tìm các hình có trục đối xứng trên hình 59.

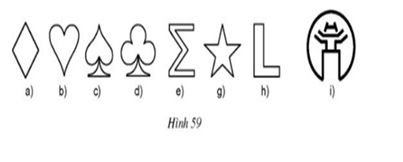
Lời giải:

- Hình h không có trục đối xứng

- Hình có 1 trục đối xứng: b, c, d, e, i

- Hình có 2 trục đối xứng: a

- Hình có 5 trục đối xứng: g

Bài 14 Cắt một tấm bìa hình tam giác cân, một tấm bìa hình thang cân. Hãy cho biết đường nào là trục đối xứng của mỗi hình, sau đó gấp mỗi tấm bìa để kiểm tra lại điều đó.

Lời giải:

- ΔABC cân tại A có trục đối xứng là đường phân giác AH của góc BAC

– Hình thang cân ABCD nhận đường thẳng HK đi qua trung điểm hai đáy làm trục đối xứng.

Bài 15 a) Cho hai điểm A, B thuộc cùng một mặt phẳng có bờ là đường thẳng d (hình 60). Gọi C là điểm đối xứng với A qua d. Gọi D là giao điểm của đường thẳng d và đoạn thẳng BC. Gọi E là điểm bất kì của đường thẳng d (E khác D).

Chứng minh: AD + DB < AE + EB.

b) Bạn Tú đang ở vị trí A, cần đến bờ sông d lấy nước rồi đi đến vị trí B (hình 60). Con đường ngắn nhất mà bạn Tú nên đi là con đường nào?

Lời giải:

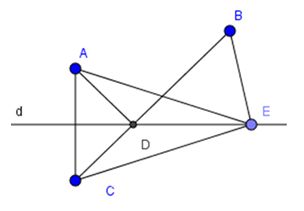
a) Vì A và C đối xứng qua d

Suy ra d là trung trực của AC => AD = CD

Nên AD + DB = CD + DB = CB         (1)

Và AE = CE (d là trung trực của AC)

Nên AE + EB = CE + EB         (2)

Lại có CB < CE + EB         (3)

từ (1), (2), (3) suy ra AD + DB < AE + EB

b) Theo ý a con đường ngắn nhất mà bạn Tú phải đi là con đường ADB.

III. Bài tập vận dụng

Bài 1 Tính diện tích hình bình hành ABCD biết AD = 6cm, AB = 10cm và $\hat{A}$=150∘

Bài 2 Trong các biển báo giao thông sau đây, biển nào có trục đối xứng?

a) Biển nguy hiểm: Đường hẹp hai bên (h.61a)

b) Biển nguy hiểm: Đường giao thông với đường sắt có rào chắn (h.61b)

c) Biển nguy hiểm: Đường ưu tiên gặp đường không ưu tiên bên phải (h.61c)

d) Biển nguy hiểm khác (d.61d)

Bài 3 Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở h.71 có là hình bình hành không?

Bài 4 Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF

Bài 5 Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF

b) Tứ giác DEBF là hình gì? Vì sao?

Bài 6 Các câu sau đúng hay sai?

a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành

b) Hình thang có hai cạnh bên song song là hình bình hành

c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành

d) Hình thang có hai cạnh bên bằng nhau là hình bình hành

Bài 7 Cho hình 72. Trong đó ABCD là hình bình hành

a) Chứng minh rằng AHCK là hình bình hành

b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.

Bài 8 Tứ giác ABCD có E, F , G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Bài 9 Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:

a) AI // CK

b) DM = MN = NB

Bài 10 Các cạnh đối của tứ giác ABCD trên hình 66 có gì đặc biệt?

Bài 11 Tính diện tích hình thang vuông ABCD ($\hat{A}=\hat{D}={90}^{\circ }$), biết $\hat{C}={45}^{\circ }$, AB = 2cm và CD = 4cm.

Bài 12 Tính diện tích hình thang ABCD biết AB = 3cm, BC = 8cm, CD = 12cm và $\hat{C}={30}^{\circ }$

Bài 13 Cho hình thang cân ABCD (AB // CD, AB < CD) biết chiều cao AH = 8cm và HC = 12cm.

Bài 14 Chứng minh rằng diện tích tam giác có cạnh đáy là cạnh bên của hình thang là trung điểm của cạnh bên kia thì bằng một nửa diện tích của hình thang đó.

Bài 15 Cho tam giác ABC. Từ một điểm E trên cạnh AC vẽ đường thẳng song song với BC cắt AB tại F và đường thẳng song song với AB cắt BC tại D. Giả sử AE = BF, chứng minh:

a) Tam giác AED cân                                   b) AD là phân giác của góc A.

Bài 16 Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA và I, K là trung điểm của các đường chéo AC, BD. Chứng minh:

a) Các tứ giác MNPQ, INKQ là hình bình hành.

b) Các đường thẳng MP, NQ, IK đồng quy.

Bài 17 Cho tam giác ABC, H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. 

a) Chứng minh tứ giác BDCH là hình bình hành.

b) Tính số đo góc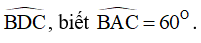 

B. Lý thuyết Hình bình hành

1. Định nghĩa

Hình bình hành là tứ giác có các cạnh đối song song

Tứ giác ABCD là hình bình hành ⇔

Chú ý đặc biệt: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song)

2. Tính chất hình bình hành

Định lí: Trong hình bình hành:

+ Các cạnh đối bằng nhau.

+ Các góc đối bằng nhau.

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

3. Dấu hiệu nhận biết hình bình hành

+ Tứ giác có các cạnh đối song song là hình bình hành.

+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

+ Tứ giác có các góc đối bằng nhau là hình bình hành.

+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

Ví dụ: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và ABEˆ = CDFˆ .

Hướng dẫn:

Xét tứ giác BEDF có

⇒ BEDF là hình bình hành

⇒ BE = DF (hai cạnh đối song song và bằng nhau)

Ta có: ABCD là hình bình hành nên BADˆ = BCDˆ       ( 1 )

BEDF là hình bình hành nên BEDˆ = DFBˆ       ( 2 )

Mà

Từ ( 2 ) và ( 3 ) ⇒ AEBˆ = DFCˆ       ( 4 )

Xét Δ ABE có BAEˆ + AEBˆ + ABEˆ = 180⁰      (5)

Xét Δ DFC có DFCˆ + FCDˆ + FDCˆ = 180⁰      (5)

Từ ( 1 ), ( 4 ), ( 5 ) ⇒ ABEˆ = CDFˆ (đpcm)