Với giải bài 44 trang 92 Toán lớp 8 chi tiết trong Bài 7: Hình bình hành giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 7: Hình bình hành
Bài 44 trang 92 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF
Lời giải:
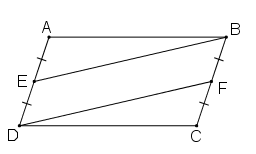
Cách 1: Sử dụng phương pháp chứng minh hai tam giác bằng nhau:
Vì ABCD là hình bình hành nên:
AB = CD (hai cạnh đối bằng nhau)
(hai góc đối bằng nhau)
AD = BC AE = ED = BF = CF (E là trung điểm của AD, F là trung điểm của BC).
Xét và , có:
AB = CD (cmt)
(cmt)
AE = CF (cmt)
⇒ ΔAEB = ΔCFD (c.g.c)
⇒ EB = DF (hai cạnh tương ứng).
Cách 2: Sử dụng phương pháp chứng minh tứ giác BEDF là hình bình hành
Vì ABCD là hình bình hành
⇒ AD//BC hay DE // BF và AD = BC.
Ta có: E là trung điểm của AD ⇒
F là trung điểm của BC ⇒
Mà AD = BC
⇒ DE = BF.
Xét tứ giác BEDF có:
DE // BF và DE = BF
⇒ BEDF là hình bình hành
⇒ BE = DF.
Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:
Câu hỏi 1 trang 90 Toán 8 Tập 1: Các cạnh đối của tứ giác ABCD trên hình 66 có gì đặc biệt?...
Bài 46 trang 92 Toán 8 Tập 1:Các câu sau đúng hay sai?...
Bài 47 trang 93 Toán 8 Tập 1: Cho hình 72. Trong đó ABCD là hình bình hành...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
