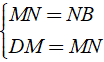Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Dấu hiệu nhận biết hình bình hành, tài liệu bao gồm 8 trang, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài kiểm tra sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây.

Lý thuyết Hình bình hành

A. Lý thuyết

1. Định nghĩa

Hình bình hành là tứ giác có các cạnh đối song song

Tứ giác ABCD là hình bình hành ⇔

Chú ý đặc biệt: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song)

2. Tính chất hình bình hành

Định lí: Trong hình bình hành:

+ Các cạnh đối bằng nhau.

+ Các góc đối bằng nhau.

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

3. Dấu hiệu nhận biết hình bình hành

+ Tứ giác có các cạnh đối song song là hình bình hành.

+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

+ Tứ giác có các góc đối bằng nhau là hình bình hành.

+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

Ví dụ: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và ABEˆ = CDFˆ .

Hướng dẫn:

Xét tứ giác BEDF có

⇒ BEDF là hình bình hành

⇒ BE = DF (hai cạnh đối song song và bằng nhau)

Ta có: ABCD là hình bình hành nên BADˆ = BCDˆ       ( 1 )

BEDF là hình bình hành nên BEDˆ = DFBˆ       ( 2 )

Mà

Từ ( 2 ) và ( 3 ) ⇒ AEBˆ = DFCˆ       ( 4 )

Xét Δ ABE có BAEˆ + AEBˆ + ABEˆ = 180⁰      (5)

Xét Δ DFC có DFCˆ + FCDˆ + FDCˆ = 180⁰      (5)

Từ ( 1 ), ( 4 ), ( 5 ) ⇒ ABEˆ = CDFˆ (đpcm)

B. Bài tập tự luyện

Bài 1: Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A,C xuống BD.

a) Chứng minh AHCK là hình bình hành.

b) Gọi O là trung điểm của HK. Chứng minh A, O, C thẳng hàng.

Hướng dẫn:

a) Từ giả thiết ta có: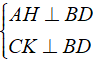 ⇒ AH//CK.      ( 1 )

Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:

 ⇒ Δ ADH = Δ CBK

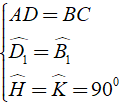
(trường hợp cạnh huyền – góc nhọn)

⇒ AH = CK (cạnh tương tứng bằng nhau)       ( 2 )

Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.

b) Áp dụng tính chất đường chéo của hình bình hành AHCK

Hình bình hành AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường

Do O là trung điểm của HK nên O cũng là trung điểm của AC

⇒ A, O, C thẳng hàng.

Bài 2: Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng:

a) AK//CI

b) DM = MN = NB

Hướng dẫn:

a) Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:

Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.

b) Theo câu a, AICK là hình bình hành

⇒ AK//CI. Khi đó , ta có:

Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:

ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:

 ⇒ DM = MN = NB