Với giải sách bài tập Toán 7 Ôn tập cuối chương 7 sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Ôn tập cuối chương 7
Giải SBT Toán 7 trang 35 Tập 2
Câu 1 trang 35 SBT Toán 7 tập 2: Biểu thức nào sau đây không là đa thức một biến?
A. ;
B. – x;
C. x + ;
D. − 1.
Lời giải:
Đáp án đúng là: C.
x + không phải đa thức một biến vì không phải là đơn thức theo biến x.
A. 4 và 0;
B. 0 và 4;
C. 4 và – 5;
D. – 5 và 4.
Lời giải:
Đáp án đúng là : A.
Vì đa thức G(x) = 4x3 + 2x2 − 5x có hạng tử có bậc cao nhất là 4x3, bậc 3, nên G(x) có hệ số cao nhất là 4 và hệ số tự do là 0.
A. f(x) và g(x) có cùng bậc;
B. f(x) có bậc lớn hơn bậc của g(x);
C. g(x) có bậc lớn hơn bậc của f(x);
D. Không bao giờ.
Lời giải:
Đáp án đúng là : B.
Trong mọi trường hợp khi f(x) có bậc lớn hơn bậc của g(x) thì bậc của f(x) + g(x) chắc chắn bằng bậc của f(x).
Câu 4 trang 35 SBT Toán 7 tập 2: Cho đa thức P(x) = x2 + 5x − 6. Khi đó:
A. P(x) chỉ có một nghiệm là x = 1;
B. P(x) không có nghiệm;
C. P(x) chỉ có một nghiệm là x = −6;
D. x = 1 và x = −6 là hai nghiệm của P(x).
Lời giải:
Đáp án đúng là: D.
Thay x = 1 và x = −6 vào P(x) ta có:
P(1) = 12 + 5.1 −6 = 1 + 5 −6 = 0
P(−6) = (−6)2 + 5.(– 6) − 6 = 36 − 30 − 6 = 0
Do đó x = 1 và x = −6 là hai nghiệm của P(x).
A. n = 0;
B. n = 1;
C. n = 2;
D. n = 3.
Lời giải:
Đáp án đúng là : D.
Đa thức đã cho chia hết cho nếu từng hạng tử của nó chia hết cho , nói riêng thì bậc của nhỏ hơn hoặc bằng bậc nhỏ nhất của đa thức.
Khi đó 7 − 2n ≤ 2 ⇔ n ≥ . Chỉ có n = 3 thỏa yêu cầu đề bài.
a) x5 + 7x2 − x − 2x5 + 3 − 5x2;
b) 4x3 − 5x2 + x − 4x3 + 3x2 − 2x + 6.
Lời giải:
a) x5 + 7x2 − x − 2x5 + 3 − 5x2
= (x5 − 2x5) + (7x2 − 5x2) − x + 3
= −x5 + 2x2 − x + 3
Vì đa thức trên có hạng tử có bậc cao nhất là −x5 nên đa thức có bậc 5, hệ số cao nhất là −1 và hệ số tự do là 3.
b) 4x3 − 5x2 + x − 4x3 + 3x2 − 2x + 6
= (4x3 − 4x3) + (−5x2 + 3x2) + (x − 2x) + 6
= −2x2 − x + 6
Vì đa thức trên có hạng tử có bậc cao nhất là −2x2 nên đa thức có bậc 2, hệ số cao nhất là −2, hệ số tự do là 6.
Giải SBT Toán 7 trang 36 Tập 2
Lời giải:
Ta có: f(x) + g(x)
= (4x4 − 5x3 + 3x + 2) + (−4x4 + 5x3 + 7)
= 4x4 − 5x3 + 3x + 2 −4x4 + 5x3 + 7
= (4x4 −4x4) + (−5x3 + 5x3) + 3x + (2 + 7)
= 3x + 9.
Để tìm nghiệm của đa thức f(x) + g(x) thì đa thức phải bằng 0.
Suy ra 3x + 9 = 0
x = (−9) : 3 = −3
Vậy nghiệm của đa thức f(x) + g(x) là x = −3
Bài 7.36 trang 36 SBT Toán 7 Tập 2: Cho hai đa thức f(x) = −x5 + 3x2 + 4x + 8 và g(x) = −x5 − 3x2 + 4x + 2. Chứng minh rằng đa thức f(x) – g(x) không có nghiệm.
Lời giải:
Ta có f(x) – g(x)
= (−x5 + 3x2 + 4x + 8) – (−x5 − 3x2 + 4x + 2)
= −x5 + 3x2 + 4x + 8 + x5 + 3x2 – 4x – 2
= (−x5 + x5) + (3x2 + 3x2) + (4x – 4x) + (8 – 2)
= 6x2 + 6
Vì f(x) – g(x) = 6x2 + 6 ≥ 6 với mọi x nên f(x) – g(x) không có nghiệm.
Bài 7.37 trang 36 SBT Toán 7 Tập 2: Cho hai đa thức sau:
P(x) = 3x5 – 2x4 + 7x2 + 3x – 10
Q(x) = –3x5 – x3 – 7x2 + 2x + 10
a) Xác định bậc, hệ số cao nhất và hệ số tự do của các đa thức
S(x) = P(x) + Q(x) và D(x) = P(x) – Q(x)
b) Trong tập hợp {–1; 0; 1}, tìm những số là nghiệm của một trong hai đa thức S(x) và D(x).
Lời giải:
a) S(x) = P(x) + Q(x)
= (3x5 – 2x4 + 7x2 + 3x – 10) + (–3x5 – x3 – 7x2 + 2x + 10)
= 3x5 – 2x4 + 7x2 + 3x – 10 – 3x5 – x3 – 7x2 + 2x + 10
= (3x5 – 3x5) – 2x4 – x3 + (7x2 – 7x2) + (3x + 2x) + (–10 + 10)
= –2x4 – x3 + 5x
S(x) = –2x4 – x3 + 5x là đa thức bậc 4 với hệ số cao nhất là –2 và hệ số tự do là 0.
D(x) = P(x) – Q(x)
= (3x5 – 2x4 + 7x2 + 3x – 10) − (–3x5 – x3 – 7x2 + 2x + 10)
= 3x5 – 2x4 + 7x2 + 3x – 10 + 3x5 + x3 + 7x2 – 2x – 10
= (3x5 + 3x5 ) – 2x4 + x3 + (7x2 + 7x2)+ (3x – 2x) + (–10 – 10)
= 6x5 – 2x4 + x3 + 14x2 + x – 20
D(x) = 6x5 – 2x4 + x3 + 14x2 + x – 20 là đa thức bậc 5 với hệ số cao nhất là 6 và hệ số tự do là – 20
b) Xét đa thức S(x):
+) Thay x = – 1 vào đa thức S(x) ta được:
S(0) = –2.(– 1)4 – (– 1)3 + 5.(– 1) = – 6 ≠ 0
Do đó x = – 1 không là nghiệm của đa thức S(x).
+) Thay x = 0 vào đa thức S(x) ta được:
S(0) = –2.04 – 03 + 5.0 = 0
Do đó x = 0 là nghiệm của đa thức S(x).
+) Thay x = 1 vào đa thức S(x) ta được:
S(0) = –2.14 – 13 + 5.1 = 2 ≠ 0
Do đó x = 1 không là nghiệm của đa thức S(x).
Xét đa thức D(x):
+) Thay x = – 1 vào đa thức D(x) ta được:
D(1) = 6.(– 1)5 – 2.(– 1)4 + (– 1)3 + 14.(– 1)2 + (– 1) – 20 = – 6 – 2 – 1 + 14 – 1 – 20 = – 16 ≠ 0.
Do đó x = – 1 không là nghiệm của đa thức D(x).
+) Thay x = 0 vào đa thức D(x) ta được:
D(1) = 6.05 – 2.04 + 03 + 14.02 + 0 – 20 = – 20 ≠ 0
Do đó x = 0 không là nghiệm của đa thức D(x).
+) Thay x = 1 vào đa thức D(x) ta được:
D(1) = 6.15 – 2.14 + 13 + 14.12 + 1 – 20 = 6 – 2 + 1 + 14 + 1 – 20 = 0
Do đó x = 1 là nghiệm của đa thức D(x).
Vậy x = 0 là nghiệm của đa thức S(x) và x = 1 là nghiệm của đa thức D(x).
Lời giải:
Gọi hai nghiệm đối nhau của f(x) là a và – a (a ≠ 0). Khi đó ta có:
f(a) = a4 + pa3 – 2a2 + 1 = 0 = f(– a) = (– a)4 + p(–a)3 – 2(–a)2 + 1
Suy ra:
a4 + pa3 – 2a2 + 1 = a4 – pa3 – 2a2 + 1
Thu gọn ta được pa3 = –pa3, suy ra 2pa3 = 0 . Do a ≠ 0 nên từ đẳng thức này suy ra p = 0.
Bài 7.39 trang 36 SBT Toán 7 Tập 2: Thực hiện các phép tính sau:
a) (5x3 – 2x2 + 4x – 4)(3x2 + x – 1);
b) (9x5 – 6x3 + 18x2 – 35x – 42) : ( 3x3 + 5x + 6);
Lời giải:
a) (5x3 – 2x2 + 4x – 4)(3x2 + x – 1)
= 3x2(5x3 – 2x2 + 4x – 4) + x(5x3 – 2x2 + 4x – 4) – 1(5x3 – 2x2 + 4x – 4)
= 15x5 – 6x4 + 12x3 – 12x2 + 5x4 – 2x3 + 4x2 – 4x – 5x3 + 2x2 – 4x + 4
= 15x5 + (–6x4 + 5x4) + (12x3 – 2x3 – 5x3) + (–12x2 + 4x2 + 2x2)+ (–4x– 4x) + 4
= 15x5 – x4 + 5x3 – 6x2 – 8x + 4
b) (9x5 – 6x3 + 18x2 – 35x – 42) : ( 3x2 + 5x + 6)
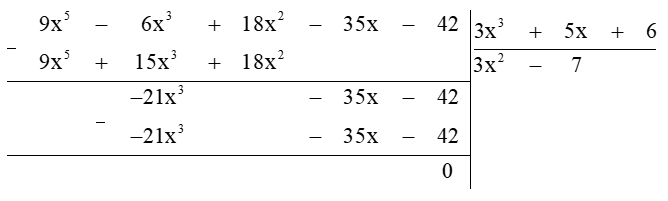
Vậy phép chia (9x5 – 6x3 + 18x2 – 35x – 42) : ( 3x2 + 5x + 6) có thương là 3x2 − 7 và dư 0.
c) : (2x – 3)
Tính (6x3 − 5x2 − 8x + 5) − (4x2 − 6x + 2)
= 6x3 − 5x2 − 8x + 5 − 4x2 + 6x − 2
= 6x3 + (−5x2 − 4x2) + (−8x + 6x) + (5 − 2)
= 6x3 − 9x2 − 2x + 3
Ta thực hiện tiếp phép chia (6x3 − 9x2 − 2x + 3) : (2x – 3)
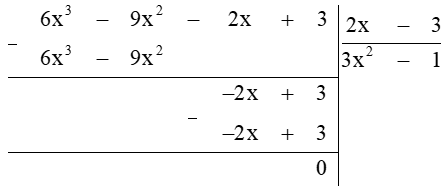
Vậy phép chia : (2x – 3) có thương là 3x2 − 1 và số dư là 0
Bài 7.40 trang 36 SBT Toán 7 Tập 2: Rút gọn các biểu thức sau:
a) A = (x − 1)(x + 2)(x − 3) − (x + 1)(x − 2)(x + 3)
b) B = (x − 1)(x + 1)( x2 + 1)(x4 +1) − x8
Lời giải:
a) A = (x − 1)(x + 2)(x − 3) − (x + 1)(x − 2)(x + 3)
Ta có:
(x − 1)(x + 2)(x − 3)
= [x(x + 2) − 1(x + 2)](x − 3)
= (x2 + 2x − x − 2)(x − 3)
= (x2 + x − 2)(x − 3)
= x(x2 + x − 2) − 3(x2 + x − 2)
= x3 + x2 − 2x − 3x2 − 3x + 6
= x3 + (x2 − 3x2) + (−2x − 3x) + 6
= x3 − 2x2 − 5x + 6 (1)
(x + 1)(x − 2)(x + 3)
= [x(x − 2) + 1(x − 2)](x + 3)
= (x2 − 2x + x − 2)(x + 3)
= (x2 − x − 2)(x + 3)
= x(x2 − x − 2) + 3(x2 − x − 2)
= x3 − x2 − 2x + 3x2 − 3x − 6
= x3 + (−x2 + 3x2) + (−2x − 3x) − 6
= x3 + 2x2 − 5x − 6 (2)
Khi đó: A = (x − 1)(x + 2)(x − 3) − (x + 1)(x − 2)(x + 3) = (1) − (2)
= (x3 − 2x2 − 5x + 6) − (x3 + 2x2 − 5x − 6)
= x3 − 2x2 − 5x + 6 − x3 − 2x2 + 5x + 6
= (x3 − x3) + (−2x2 − 2x2) + (−5x + 5x) + (6 + 6)
= −4x2 + 12.
b) B = (x − 1)(x + 1)( x2 + 1)(x4 +1) − x8
Với M là một biểu thức tùy ý, ta có:
(M − 1)(M + 1) = M2 − M + M − 1 hay (M − 1)(M + 1) = M2 − 1 (1)
Từ đó, ta có:
(x − 1)(x + 1) (áp dụng (1) với M = x)
(x2 − 1)(x2 + 1) = (x2)2 − 1 = x4 − 1 (áp dụng (1) với M = x2)
(x4 − 1)(x4 + 1) = (x4)2 − 1 = x8 − 1 (áp dụng (1) với M = x4).
Sử dụng các kết quả trên, ta được:
(x − 1)(x + 1)(x2 + 1)(x4 + 1)
= (x2 +1)(x4 + 1)
= (x2 − 1)(x2 + 1)(x4 + 1)
= (x4 + 1)
= (x4 − 1)(x4 + 1)
= x8 − 1.
Vậy B = (x − 1)(x + 1)( x2 + 1)(x4 +1) − x8 = x8 – 1 − x8 = −1.
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
SBT Toán 7 Bài 28: Phép chia đa thức một biến
SBT Toán 7 Ôn tập cuối chương 7
SBT Toán 7 Bài 29: Làm quen với biến cố
SBT Toán 7 Bài 30: Làm quen với xác suất của biến cố
1. Biểu thức đại số
• Biểu thức không chứa chữ gọi là biểu thức số.
• Biểu thức chỉ chứa số hoặc chỉ chứa chữ hoặc chứa cả số và chữ gọi chung là biểu thức đại số.
• Trong một biểu thức đại số, các chữ (nếu có) dùng để thay thế hay đại diện cho những số nào đó được gọi là các biến số (gọi tắt là các biến).
• Một biểu thức đại số có thể chứa nhiều biến khác nhau.
Chú ý:
• Để cho gọn khi viết các biểu thức đại số, ta không viết dấu nhân giữa các biến, cũng như giữa biến và số.
Chẳng hạn, x.y viết là xy; 7.a viết là 7a.
• Thông thường ta không viết thừa số 1 trong các tích.
Chẳng hạn, 1x2 viết là x2; (– 1)xy viết là – xy.
• Với các biến, ta cũng có thể áp dụng các quy tắc và tính chất của các phép tính như đối với các số.
2. Giá trị của biểu thức đại số
• Muốn tính giá trị của một biểu thức đại số tại những giá trị cho trước của các biến, ta thay giá trị đã cho của mỗi biến vào biểu thức rồi thực hiện các phép tính.
3. Đơn thức một biến
• Đơn thức một biến (gọi tắt là đơn thức) là biểu thức đại số có dạng tích của một số thực với một lũy thừa của biến, trong đó số thực gọi là hệ số, số mũ của lũy thừa của biến gọi là bậc của đơn thức.
• Cộng (hay trừ) hai đơn thức cùng bậc bằng cách cộng (hay trừ) các hệ số với nhau và giữ nguyên lũy thừa của biến. Tổng nhận được là một đơn thức.
• Nhân hai đơn thức tùy ý bằng cách nhân hai hệ số với nhau và nhân hai lũy thừa của biến với nhau. Tích nhận được là một đơn thức.
Chú ý:
• Một số khác 0 được gọi là đơn thức bậc 0.
Chẳng hạn, số 3 là đơn thức bậc 0 vì có thể coi 3 = 3x0.
• Số 0 cũng được coi là một đơn thức. Đơn thức này không có bậc.
4. Khái niệm đa thức một biến
• Đa thức một biến (gọi tắt là đa thức) là tổng của những đơn thức của cùng một biến; mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
• Một đơn thức cũng là một đa thức.
• Số 0 cũng được coi là một đa thức, gọi là đa thức không.
Chú ý:
• Ta thường kí hiệu đa thức bằng một chữ cái in hoa. Đôi khi còn viết thêm kí hiệu biến trong ngoặc đơn.
Chẳng hạn: M = M(x) = x3 – 2x2 + 7x+ 1.
5. Đa thức một biến thu gọn
• Đa thức thu gọn là đa thức không chứa hai đơn thức nào cùng bậc.
• Nếu một đa thức có chứa những đơn thức cùng bậc (đa thức chưa thu gọn) thì ta có thể đưa nó về dạng thu gọn.
6. Sắp xếp đa thức một biến
Đối với các đa thức khác đa thức 0, để thuận lợi cho việc tính toán các đa thức một biến, người ta thường viết chúng dưới dạng thu gọn và sắp xếp các hạng tử của nó theo lũy thừa giảm dần của biến.
Chú ý: Ta có thể sắp xếp đa thức theo lũy thừa tăng dần của biến.
7. Bậc và các hệ số của một đa thức
Trong một đa thức thu gọn và khác đa thức 0:
• Bậc của hạng tử có bậc cao nhất gọi là bậc của đa thức đó.
• Hệ số của hạng tử có bậc cao nhất gọi là hệ số cao nhất của đa thức đó.
• Hệ số của hạng tử bậc 0 gọi là hệ số tự do của đa thức đó.
Chú ý:
• Đa thức không là đa thức không có bậc.
• Trong một đa thức thu gọn, hệ số cao nhất phải khác 0 (các hệ số khác có thể bằng 0).
• Muốn tìm bậc của một đa thức chưa thu gọn, ta phải thu gọn đa thức đó.
8. Nghiệm của đa thức một biến
• Nếu tại x = a (a là một số), đa thức F(x) có giá trị bằng 0, tức là F(a) = 0, thì ta gọi a (hoặc x = a) là một nghiệm của đa thức F(x).
• Một đa thức có thể có nhiều nghiệm hoặc không có nghiệm.
• Một đa thức có hệ số tự do bằng 0 thì x = 0 là một nghiệm của đa thức đó.
9. Cộng hai đa thức một biến
• Cách 1: Viết hai đa thức trong dấu ngoặc rồi nối chúng bởi dấu “+”. Sau đó bỏ ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.
• Cách 2: Đặt tính cộng sao cho các hạng tử cùng bậc của hai đa thức thì thẳng cột với nhau rồi cộng theo từng cột. Nếu đa thức khuyết một hạng tử bậc nào đó thì ta để một khoảng trống ứng với hạng tử đó.
Chú ý: Phép cộng đa thức cũng có tính chất như phép cộng số thực. Cụ thể là:
+ Tính chất giao hoán: A + B = B + A;
+ Tính chất kết hợp: (A + B) + C = A + (B + C);
+ Cộng với đa thức không: A + 0 = 0 + A = A.
10. Trừ hai đa thức một biến
• Cách 1: Viết hai đa thức trong dấu ngoặc rồi nối chúng bởi dấu “–”. Sau đó bỏ ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.
• Cách 2: Đặt tính trừ sao cho các hạng tử cùng bậc của hai đa thức thì thẳng cột với nhau rồi trừ theo từng cột. Nếu đa thức khuyết một hạng tử bậc nào đó thì ta để một khoảng trống ứng với hạng tử đó.
Chú ý: Tương tự như các số, với các đa thức P, Q và R, ta cũng có:
- Nếu Q + R = P thì R = P – Q.
- Nếu R = P – Q thì Q + R = P.
11. Nhân đơn thức với đa thức
Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức vời từng hạng tử của đa thức rồi cộng các tích với nhau.
12. Nhân đa thức với đa thức
Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Chú ý:
• Ta có thể trình bày phép nhân một đa thức với một đa thức bằng cách đặt tính.
Khi trình bày theo cách này ta cần:
+ Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trong một dòng riêng.
+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau (để thực hiện phép cộng theo cột).
+ Khi nhân các hạng tử ở dòng dưới với đa thức ở dòng trên, ta nên nhân các hạng tử theo thứ tự từ bậc thấp đến bậc cao.
Chẳng hạn: Đặt tính nhân (x + 3).(2x2 – 3x – 5), ta làm như sau:
• Phép nhân đa thức cũng có các tính chất:
+ Giao hoán: A.B = B.A.
+ Kết hợp: (A.B).C = A.(B.C).
+ Phân phối đối với phép cộng: A.(B + C) = A.B + A.C.
13. Làm quen phép chia đa thức
• Cho hai đa thức A và B (B ≠ 0). Nếu có một đa thức Q sao cho A = B.Q thì ta có phép chia hết:
A : B = Q (hay ), trong đó
A là đa thức bị chia;
B là đa thức chia (kí hiệu B ≠ 0 có nghĩa B không phải là đa thức không).
Q là đa thức thương (gọi tắt là thương).
Khi đó ta còn nói đa thức A chia hết cho đa thức B.
• Cho hai đơn thức axm và bxn (m; n ∈ ℕ, a; b ∈ ℝ, b ≠ 0).
Khi đó nếu m ≥ n thì ta có phép chia axm cho bxn là phép chia hết và ta có:
axm : bxn = xm – n (quy ước: x0 = 1).
Chú ý:
• axm : bxn được hiểu là axm : (bxn)
Chẳng hạn: 4x5 : 2x2 được hiểu là 4x5 : (2x2).
14. Chia đa thức cho đa thức
• Muốn chia một đa thức cho một đa thức, ta đặt tính và chia (tương tự phép chia hai số tự nhiên) cho đến khi được đa thức dư là đa thức không, hoặc có bậc nhỏ hơn bậc của đa thức chia.
• Khi đặt tính chia, nếu đa thức ở một dòng khuyết một hạng tử bậc nào đó thì ta để một khoảng trống ứng với hạng tử đó.
• Nếu chia đa thức A cho đa thức B, ta được đa thức thương là Q, đa thức dư là R thì:
+ Đa thức dư R = 0 (khi chia hết) hoặc R là đa thức có bậc nhỏ hơn đa thức B (nếu không chia hết).
+ Ta có đẳng thức: A = B.Q + R.
Chú ý: Khi chia đa thức cho một đơn thức có thể không cần đặt tính chia.