Với giải sách bài tập Toán 7 Ôn tập chương 8 sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Ôn tập chương 8

Giải SBT Toán 7 trang 44 Tập 2

Câu 1 trang 44 SBT Toán 7 tập 2: Biến cố “Nhiệt độ cao nhất trong tháng Sáu năm sau tại Thành phố Hồ Chí Minh là 10 ^oC” là

A. Biến cố chắc chắn;

B. Biến cố ngẫu nhiên;

C. Biến cố không thể;

D. Biến cố đồng khả năng.

Lời giải:

Đáp án đúng là: C

Nhiệt độ vào tháng Sáu hàng năm luôn trên 23 ^oC.

Do đó biến cố “Nhiệt độ cao nhất trong tháng Sáu năm sau tại Thành phố Hồ Chí Minh là 10 ^oC” là biến cố không thể.

Câu 2 trang 44 SBT Toán 7 tập 2: Biến cố “Ngày mai có mưa rào và giông ở Hà Nội” là:

A. Biến cố ngẫu nhiên;

B. Biến cố chắc chắn;

C. Biến cố đồng khả năng;

D. Biến cố không thể.

Lời giải:

Đáp án đúng là: A

Biến cố “Ngày mai có mưa rào và giông ở Hà Nội” là biến cố ngẫu nhiên vì điều này không chắc có thể xảy ra.

Câu 3 trang 44 SBT Toán 7 tập 2: Hai túi I và II chứa các tấm thẻ được ghi số 3; 4; 5; 6; 7. Từ mỗi túi rút ngẫu nhiên một tấm thẻ.

a) Xác suất của biến cố “Tích hai số ghi trên hai tấm thẻ lớn hơn 8” bằng

A. 0;

B. $\frac{1}{2}$ ;

C. 1;

D. 0,25.

Đáp án đúng là: C

Lời giải:

Tích của hai số trên hai tấm thẻ nhỏ nhất là: 3 . 4 = 12.

Do đó tích của hai số ghi trên hai tấm thẻ luôn lớn hơn hoặc bằng 12 nên sẽ luôn lớn hơn 8 hay biến cố đã cho là biến cố chắc chắn.

Vậy xác suất của biến cố “Tích hai số ghi trên hai tấm thẻ lớn hơn 8” bằng 1.

b) Xác xuất của biến cố “Tổng hai số ghi trên hai tấm thẻ nhỏ hơn 5” bằng

A. 1;

B. 0;

C. 0,45;

D. 0,5.

Đáp án đúng là: B

Lời giải:

Tổng của hai số trên hai tấm thẻ nhỏ nhất là: 3 + 4 = 7.

Do đó tổng của hai số ghi trên hai tấm thẻ luôn lớn hơn hoặc bằng 7 nên biến cố đã cho là biến cố không thể.

Vậy xác suất của biến cố “Tổng hai số ghi trên hai tấm thẻ nhỏ hơn 5” bằng 0.

c) Biến cố “Hiệu hai số ghi trên hai tấm thẻ là số chẵn” là

A. Biến cố ngẫu nhiên;

B. Biến cố chắc chắn;

C. Biến cố không thể;

D. Biến cố đồng khả năng.

Đáp án đúng là: A

Lời giải:

Biến cố “Hiệu hai số ghi trên hai tấm thẻ là số chẵn” là biến cố ngẫu nhiên vì điều này không chắc có thể xảy ra. (Ví dụ hiệu của hai số 4 và 3 là 1).

Câu 4 trang 44 SBT Toán 7 tập 2: Một thùng kín có 20 quả bóng màu đỏ và 20 quả bóng màu xanh. Sơn lấy ngẫu nhiên một quả bóng trong thùng.

a) Xác suất của biến cố “Lấy được quả bóng màu xanh” bằng

A. 1;

B. $\frac{1}{2}$ ;

C. 0;

D. 0,8.

Đáp án đúng là: B

Lời giải:

Biến cố “Lấy được quả bóng màu xanh” và biến cố “Lấy được quả bóng màu đỏ” là đồng khả năng vì số bóng xanh bằng với số bóng đỏ. Vậy xác suất của biến cố “Lấy được quả bóng màu xanh” là $\frac{1}{2}$ .

b) Xác suất của biến cố “Lấy được quả bóng màu đỏ” bằng

A. 0

B. 1

C. 0,5

D. 0,2

Đáp án đúng là: C

Lời giải:

Biến cố “Lấy được quả bóng màu đỏ” và biến cố “Lấy được quả bóng màu xanh” là đồng khả năng vì số bóng đỏ bằng với số bóng xanh.

Vậy xác suất của biến cố cố “Lấy được quả bóng màu đỏ” là 0,5.

c) Xác suất của biến cố “Lấy được quả bóng màu đỏ hoặc màu xanh” bằng

A. 1

B. 0

C. 0,5

D. 0,4

Đáp án đúng là: A

Lời giải:

Trong tất cả những quả bóng ở trong thùng chỉ có hai màu đỏ và xanh.

Do đó biến cố “Lấy được quả bóng màu đỏ hoặc màu xanh” là biến cố chắc chắn.

Vậy xác suất của biến cố đã cho bằng 1.

Giải SBT Toán 7 trang 45 Tập 2

Bài 8.10 trang 45 SBT Toán 7 Tập 2: Một bài thi trắc nghiệm có 18 câu hỏi được đánh số từ 1 đến 18. Chọn ngẫu nhiên một câu hỏi trong bài thi.

a) Xét hai biến cố sau:

A: “Số thứ tự của câu hỏi được chọn là số có một chữ số”;

B: “Số thứ tự của câu hỏi được chọn là số có hai chữ số”.

Hai biến cố A và B có đồng khả năng không? Tại sao?

b) Tính xác suất của hai biến cố A và B.

Lời giải:

a) Hai biến cố A và B đồng khả năng vì số lượng câu hỏi mang số thứ tự là số có một chữ số bằng số lượng câu hỏi mang số thứ tự là số có hai chữ số và đều bằng 9 câu.

b) Biến biến cố A và B đồng khả năng.

Do đó xác suất của biến cố A và B bằng nhau và đều bằng $\frac{1}{2}$ .

Bài 8.11 trang 45 SBT Toán 7 Tập 2: Một tấm bài cứng hình tròn được chia làm tám phần có diện tích bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8; được gắn vào trục quay có mũi tên ở tâm như Hình 8.3.

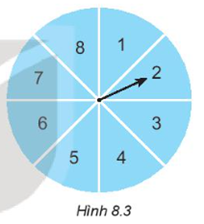
Bạn Hùng quay tấm bìa. Tính xác suất để:

a) Mũi tên dừng ở hình quạt ghi số nhỏ hơn 9;

b) Mũi tên đừng ở hình quạt ghi số 0;

c) Mũi tên dừng ở hình quạt ghi số chẵn;

d) Mũi tên dừng ở hình quạt ghi số 7 hoặc 8.

Lời giải:

a) Xác suất bằng 1 vì đây là biến cố chắc chắn (tất cả các hình quạt đều ghi số nhro hơn 9).

b) Xác suất bằng 0 vì đây là biến cố không thể (không có hình quạt nào ghi số 0).

c) Biến cố “Mũi tên dừng ở hình quạt ghi số chẵn” và biến cố “mũi tên dừng ở hình quạt ghi số lẻ” là đồng khả năng.

Vậy xác suất của biến cố cần tìm là $\frac{1}{2}$ .

d) Xét bốn biến cố sau:

A: “Mũi tên dừng ở hình quạt ghi số 1 hoặc 2”;

B: “Mũi tên dừng ở hình quạt ghi số 3 hoặc 4”;

C: “Mũi tên dừng ở hình quạt ghi số 5 hoặc 6”;

D: “Mũi tên dừng ở hình quạt ghi số 7 hoặc 8”;

Biến cố A xảy ra khi mũi tên dừng ở hình quạt ghi số 1 hoặc số 2.

Biến cố B xảy ra khi mũi tên dừng ở hình quạt ghi số 3 hoặc số 4.

Biến cố C xảy ra khi mũi tên dừng ở hình quạt ghi số 5 hoặc số 6.

Biến cố D xảy ra khi mũi tên dừng ở hình quạt ghi số 7 hoặc số 8.

Vì quay ngẫu nhiên nên mỗi hình quạt có khả năng quay được như nhau.

Do đó bốn biến cố A, B, C, D là đồng khả năng. Vì luôn xảy ra duy nhất một trong bốn biến cố này nên xác suất của biến cố D là $\frac{1}{4}$ .

Vậy xác suất của biến cố “Lấy được quả cầu ghi số 7 hoặc 8” là $\frac{1}{4}$ .

Bài 8.12 trang 45 SBT Toán 7 Tập 2: Một hộp đựng 14 quả cầu được đánh các số 10; 11; …; 23. Lẫy ngẫu nhiên một quả cầu trong hộp. Tính xác suất để:

a) Quả cầu lấy được ghi số 24;

b) Quả cầu lấy được ghi số lẻ;

c) Quả cầu lấy được ghi số 11;

d) Quả cầu lấy được mang số 12 hoặc 13.

Lời giải:

a) Hộp đựng 14 quả cầu được đánh các số 10; 11; …; 23 nên không có quả cầu nào đánh số 24.

Do đó biến cố “Quả cầu lấy được ghi số 24” là biến cố không thể.

Vậy xác suất biến cố đã cho bằng 0.

b) Biến cố “Quả cầu lấy được ghi số chẵn” và biến cố “Quả cầu lấy được ghi số lẻ” là đồng khả năng.

Vậy xác suất của biến cố cần tìm là $\frac{1}{2}$ .

c) Mỗi quả cầu có khả năng lấy được như nhau. Có 14 biến cố đồng khả năng. Vậy xác suất của biến cố đang xét là $\frac{1}{14}$ .

d) Xét 7 biến cố sau:

A: “Quả cầu lấy được mang số 10 hoặc 11”;

B: “Quả cầu lấy được mang số 12 hoặc 13”;

C: “Quả cầu lấy được mang số 14 hoặc 15”;

D: “Quả cầu lấy được mang số 16 hoặc 17”;

E: “Quả cầu lấy được mang số 18 hoặc 19”;

F: “Quả cầu lấy được mang số 20 hoặc 21”;

G: “Quả cầu lấy được mang số 22 hoặc 23”;

Biến cố A xảy ra khi lấy được quả cầu mang số 10 và 11.

Biến cố B xảy ra khi lấy được quả cầu mang số 12 và 13.

Biến cố C xảy ra khi lấy được quả cầu mang số 14 và 15.

Biến cố D xảy ra khi lấy được quả cầu mang số 16 và 17.

Biến cố E xảy ra khi lấy được quả cầu mang số 18 và 19.

Biến cố F xảy ra khi lấy được quả cầu mang số 20 và 21.

Biến cố G xảy ra khi lấy được quả cầu mang số 22 và 23. 

Do lấy ngẫu nhiên nên mỗi quả cầu có khả năng rút được như nhau.

Do đó bảy biến cố A, B, C, D, E, F, G là đồng khả năng. Vì luôn xảy ra duy nhất một trong bảy biến cố này nên xác suất của biến cố B đang xét là $\frac{1}{7}$ .

Vậy xác suất của biến cố “Quả cầu lấy được mang số 12 hoặc 13” là $\frac{1}{7}$ .

Bài 8.13 trang 45 SBT Toán 7 Tập 2: Một hộp đựng 20 quả bóng có cùng kích thước, khác nhau về màu sắc trong đó có 4 quả bóng màu xanh, 4 quả bóng màu đỏ, 4 quả bóng màu tím, 4 quả bóng màu vàng và 4 quả bóng màu trắng. Bạn Minh lấy ngẫu nhiên một quả bóng từ trong hộp.

Xét 5 biến cố sau:

A: “Minh lấy được quả bóng màu xanh”;

B: “Minh lấy được quả bóng màu đỏ”;

C: “Minh lấy được quả bóng màu tím”;

D: “Minh lấy được quả bóng màu vàng”;

E: “Minh lấy được quả bóng màu trắng”;

a) Hãy giải thích vì sao các biến cố A, B, C, D, E là đồng khả năng.

b) Tính xác suất của các biến cố A, B, C, D, E.

Lời giải:

a) Mỗi quả bóng có khả năng được chọn như nhau. Số quả bóng màu xanh, màu đỏ, màu tím, màu vàng và màu trắng bằng nhau nên các biến cố A, B, C, D, E là đồng khả năng.

b) Vì luôn xảy ra duy nhất một biến cố trong năm biến cố này nên xác suất của năm biến cố bằng nhau và bằng $\frac{1}{5}$ .

Giải SBT Toán 7 trang 46 Tập 2

Bài 8.14 trang 46 SBT Toán 7 Tập 2: Một thùng kín có 40 quả bóng cùng kích thước, một số quả có màu trắng và một số quả có màu đen. Sơn lấy ngẫu nhiên một quả bóng trong thùng. Biết rằng biến cố “Sơn chọn được quả bóng màu trắng” và biến cố “Sơn chọn được quả bóng màu đen” là đồng khả năng. Hỏi trong thùng chứa bao nhiêu quả bóng màu trắng.

Lời giải:

Biến cố “Sơn chọn được quả bóng màu trắng” và biến cố “Sơn chọn được quả bóng màu đen” là đồng khả năng . Do đó, số quả bóng màu trắng bằng số quả bóng màu đen. Vậy trong thùng chứa 20 quả bóng màu trắng.

Bài 8.15 trang 46 SBT Toán 7 Tập 2: Một chuyến xe khách có 28 hành khách nam và 31 hành khách nữ. Đến một bến xe có một số hành khách nữ xuống xe. Chọn ngẫu nhiên một hành khách còn lại trên xe. Biết rằng xác suất để chọn được hành khách nữ là $\frac{1}{2}$ . Hỏi có bao nhiêu hành khách nữ đã xuống xe?

Lời giải:

Gọi n (người) là số hành khách nữ xuống xe (n $\in$ ℕ*) . Khi đó, trên xe còn 31 – n hành khách nữ và 28 hành khách nam.

Xác suất để chọn được hành khách nữ là $\frac{1}{2}$  nên số hành khách nữ còn lại trên xe bằng số hành khách nam. Do đó, 31 – n = 28

Suy ra n = 3.

Vậy số hành khách nữ đã xuống xe là 3 người.

Bài 8.16 trang 46 SBT Toán 7 Tập 2: Một chiếc hộp chứa 50 viên bi cùng kích thước gồm một số viên bi màu xanh; một số viên bi màu đỏ; một số viên bi màu trắng; một số viên bi màu tím và một số viên bi màu vàng. Bạn Bình lấy ngẫu nhiên một viên bi trong hộp. Biết rằng 5 biến cố sau đây là đồng khả năng:

A: “Bình lấy được viên bi màu xanh”;

B: “Bình lấy được viên bi màu đỏ”;

C: “Bình lấy được viên bi màu trắng”;

D: “Bình lấy được viên bi màu tím”;

E: “Bình lấy được viên bi màu vàng”;

Hỏi trong hộp chứa bao nhiêu viên bi mỗi loại?

Lời giải:

Do lấy ngẫu nhiên nên mỗi viên bi có khả năng được lấy như nhau.

Do đó số viên bi màu xanh, số viên bi màu đỏ, số viên bi màu trắng, số viên bi màu tím và số viên bi màu vàng bằng nhau.

Vậy trong hộp mỗi loại có 10 viên bi.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 30: Làm quen với xác suất của biến cố

Ôn tập chương 8

Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác

Bài 32: Quan hệ giữa đường vuông góc và đường xiên

Bài 33: Quan hệ giữa ba cạnh trong một tam giác

Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

Tổng hợp lý thuyết Toán 7 Chương 8

1. Biến cố

Các hiện tượng, sự kiện trong tự nhiên, cuộc sống được gọi chung là biến cố.

Biến cố chắc chắn là biến cố biết trước được luôn xảy ra.

Biến cố không thể là biến cố biết trước được không bao giờ xảy ra.

Biến cố ngẫu nhiên là biến cố không thể biết trước được có xảy ra hay không.

2. Xác suất của biến cố

Khả năng xảy ra của một biến cố được đo lường bởi một số nhận giá trị từ 0 đến 1, gọi là xác suất của biến cố đó.

Nhận xét: Xác suất của một biến cố càng gần 1 thì biến cố đó càng có nhiều khả năng xảy ra. Xác suất của một biến cố càng gần 0 thì biến cố đó càng ít khả năng xảy ra.

3. Xác suất của một số biến cố đơn giản

a. Xác suất của biến cố chắc chắn, biến cố không thể

Khả năng xảy ra của biến cố chắc chắn là 100%. Vậy biến cố chắc chắn có xác suất bằng 1.

Khả năng xảy ra của biến cố không thể là 0%. Vậy biến cố không thể có xác suất bằng 0.

b. Xác suất của các biến cố đồng khả năng

∙ Gieo một đồng xu cân đối. Xét hai biến cố sau:

A: “Đồng xu xuất hiện mặt ngửa”.

B: “Đồng xu xuất hiện mặt sấp”.

Do đồng xu cân đối nên biến cố A và biến cố B có khả năng xảy ra như nhau. Ta nói hai biến cố A và B là đồng khả năng.

Vì chỉ xảy ra hoặc biến cố A hoặc biến cố B nên xác suất của biến cố A và xác suất của biến cố B bằng nhau và bằng $\frac{1}{2}$ (hay 50%).

∙ Trong một trò chơi hay thí nghiệm, nếu có k biến cố đồng khả năng và luôn xảy ra duy nhất một biến cố trong k biến cố này thì xác suất của mỗi biến cố đó đều bằng $\frac{1}{k}$.