Với giải sách bài tập Toán 7 Bài 24: Biểu thức đại số sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 24: Biểu thức đại số

Giải Toán 7 trang 20 Tập 2

Bài 7.1 trang 20 Toán 7 Tập 2: Viết biểu thức đại số biểu thị:

a) Hiệu các bình phương của hai số a và b;

b) Tổng các lập phương của hai số x và y.

Lời giải:

a) Hiệu các bình phương của hai số a và b là a² − b².

b) Tổng các lập phương của x và y là x³ + y³.

Giải Toán 7 trang 21 Tập 2

Bài 7.2 trang 21 Toán 7 Tập 2: Viết biểu thức đại số biểu thị:

a) Thể tích của hình hộp chữ nhật có chiều dài a, chiều rộng b và chiều cao là a + b.

b) Diện tích của hình tứ giác có hai đường chéo vuông góc với nhau và độ dài của hai đường chéo đó là p và q.

Lời giải:

a) Thể tích của hình hộp chữ nhật bằng chiều dài nhân chiều rộng nhân chiều cao nên ta có biểu thức đại số :

V = ab(a + b).

b) Kẻ tứ giác ABCD có hai đường chéo vuông góc cắt nhau tại H (như hình vẽ)

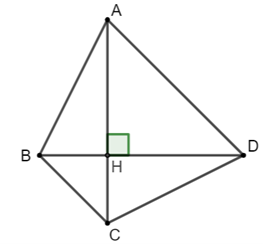
Diện tích tứ giác ABCD bằng tổng diện tích  hai tam giác ABD và tam giác BCD.

S_ABD = $\frac{1}{2}$ AH. BD

S_BCD = $\frac{1}{2}$ CH.BD

S_ABCD = S_ABD + S_BCD = $\frac{1}{2}$ AH. BD + $\frac{1}{2}$ CH.BD = $\frac{1}{2}$ (AH + CH).BD = $\frac{1}{2}$ AC.BD = $\frac{1}{2}$ pq.

Vậy biểu thức biểu thị diện tích của hình tam giác là S = $\frac{1}{2}$ pq.

Bài 7.3 trang 21 Toán 7 Tập 2: Hãy chỉ ra các biến trong mỗi biểu thức đại số thu được ở các Bài 7.1 và 7.2.

Lời giải:

Biểu thức đại số bài 7.1a là a² − b² có biến a và b.

Biểu thức đại số bài 7.1b là x³ + y³ có biến x và y.

Biểu thức đại số bài 7.2a là V = ab(a + b) có biến a và b.

Biểu thức đại số bài 7.1b là S = $\frac{1}{2}$ pq có biến p và q.

Bài 7.4 trang 21 Toán 7 Tập 2: Tính giá trị của biểu thức:

a) 2a²b + ab² − 3ab tại a = −2 và b = 4.

b) xy(x + y) −(x² + y²) tại x = 0,5 và y = −1,5

Lời giải:

a) Thay a = −2 và b = 4 vào biểu thức 2a²b + ab² − 3ab ta được:

2.(−2)².4 + (−2). 4² − 3.(−2).4 = 2.4.4 + (−2). 16 − 3.(−2).4 = 32 − 32 + 24 = 24.

b) Thay x = 0,5 và y = −1,5 vào biểu thức xy(x + y) − (x² + y²) ta được :

0,5.(−1,5)(0,5 − 1,5) − [0,5² + (−1,5)²] = 0,5.(−1,5)(−1) − [0,5² + (−1,5)²] = 0,75 − 2,5 = −1,75

Bài 7.5 trang 21 Toán 7 Tập 2: Trong hai kết luận sau, kết luận nào đúng?

a) Hai biểu thức A(x) = (x + 1)² và B(x) = x² + 1 bằng nhau với mọi giá trị của x.

(Chẳng hạn, khi x = 0 thì ta có A(0) = B(0) = 1).

b) Hai biểu thức C = a(b + c) và D = ab + ac bằng nhau với mọi giá trị của các biến a, b và c.

 (Chẳng hạn, khi a = b = c = 0 thì C = D = 0).

Lời giải:

a) Sai. Chẳng hạn tại x = 1, ta có:

A(1) = (1 + 1)² = 2² = 4.

B(1) = 1² + 1 = 1 + 1 = 2.

Vì A(1) khác B(1) nên kết luận trên là sai.

b) Đúng. Vì đẳng thức a(b + c) = ab + ac biểu thị tính chất phân phối của phép nhân và phép cộng.

Bài 7.6 trang 21 Toán 7 Tập 2: Một luống rau có x hàng, mỗi hàng có y cây rau (x, y $\in$ ℕ) . Trong tình huống này, biểu thức P = xy biểu thị số cây rau được trồng trên luống rau đó. Hãy nêu một tình huống khác, trong đó một đại lượng được biểu thị bởi biểu thức x – y.

Lời giải:

Bạn An có x nghìn đồng được mẹ nhờ đi chợ. Bạn mua hết y nghìn đồng và vẫn còn tiền thừa.

Vậy biểu thức N = x – y là số tiền thừa sau khi bạn An đi chợ.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Ôn tập cuối chương 6

Bài 24: Biểu thức đại số

Bài 25: Đa thức một biến

Bài 26: Phép cộng và phép trừ đa thức một biến

Bài 27: Phép nhân đa thức một biến

Lý thuyết Biểu thức đại số

1. Biểu thức đại số

• Biểu thức không chứa chữ gọi là biểu thức số.

• Biểu thức chỉ chứa số hoặc chỉ chứa chữ hoặc chứa cả số và chữ gọi chung là biểu thức đại số.

• Trong một biểu thức đại số, các chữ (nếu có) dùng để thay thế hay đại diện cho những số nào đó được gọi là các biến số (gọi tắt là các biến).

• Một biểu thức đại số có thể chứa nhiều biến khác nhau.

Ví dụ:

+ Biểu thức số: 29 + 6.7; 45 : 5 – 3.(6 + 4);

+ Biểu thức đại số:

- chỉ chứa số: 94 – 3².5;

- chỉ chứa chữ: x.y – x + y;

- chứa cả số và chữ: (x² + $\frac{x}{4}$) – 5;

+ Biểu thức đại số: x² – x.y + 2.y – 1 thì x và y được gọi là các biến số.

+ Biểu thức đại số: y³ +1 có 1 biến là y.

+ Biểu thức đại số: x² + y – z³ + 2 có 3 biến là x; y và z.

Chú ý:

• Để cho gọn khi viết các biểu thức đại số, ta không viết dấu nhân giữa các biến, cũng như giữa biến và số.

Chẳng hạn, x.y viết là xy; 7.a viết là 7a.

• Thông thường ta không viết thừa số 1 trong các tích.

Chẳng hạn, 1x² viết là x²; (– 1)xy viết là – xy.

• Với các biến, ta cũng có thể áp dụng các quy tắc và tính chất của các phép tính như đối với các số.

Chẳng hạn:

x + x = 2x;

x + y = y + x;

(x + y) + z = x + (y + z);

x + 0 = 0 + x = 0;

x – x = 0;

–(x + y – z) = – x – y + z;

xy = yx;

1x = x1 = x;

x0 = 0x = 0;

x(y ± z) = xy ± xz;

xx = x²;

…

2. Giá trị của biểu thức đại số

• Muốn tính giá trị của một biểu thức đại số tại những giá trị cho trước của các biến, ta thay giá trị đã cho của mỗi biến vào biểu thức rồi thực hiện các phép tính.

Ví dụ:

+ Muốn tính giá trị của biểu thức: A = 4x² – 1 tại x = 2 ta làm như sau

Thay x = 2 vào biểu thức A, ta được:

A = 4.2² – 1 = 4.4 – 1 = 16 – 1 = 15

Vậy 15 là giá trị của biểu thức A tại x = 2.

(hay: khi x = 2 thì giá trị của biểu thức A là 15).