Sách bài tập Toán 9 (Chân trời sáng tạo): Bài tập cuối chương 5

Thuy Quynh Ngày: 27-09-2024 Lớp 9

Với giải sách bài tập Toán 9 Bài tập cuối chương 5 sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:

Giải SBT Toán 9 Bài tập cuối chương 5

CÂU HỎI TRẮC NGHIỆM

Trong các câu từ 1 đến 9, chọn phương án đúng.

Câu 1 trang 98 sách bài tập Toán 9 Tập 1: Số đo góc $\hat{B A C}$ trong Hình 1 là

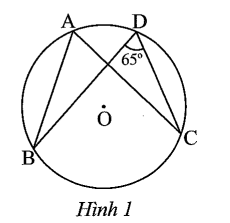
Số đo góc BAC trong Hình 1 là trang 98 sách bài tập Toán 9 Tập 1

A. 55°.

B. 32,5°.

C. 65°.

D. 25°.

Lời giải:

Đáp án đúng là: C

Ta có: $\hat{B A C} = \hat{B D C} = 65 °$ (hai góc nội tiếp đường tròn cùng chắn dây cung BC).

Câu 2 trang 98 sách bài tập Toán 9 Tập 1: Số đo góc $\hat{B A C}$ trong Hình 2 là

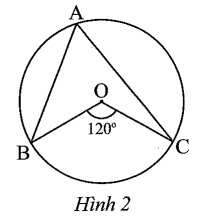
Số đo góc BAC trong Hình 2 là trang 98 sách bài tập Toán 9 Tập 1

A. 50°.

B. 70°.

C. 30°.

D. 60°.

Lời giải:

Đáp án đúng là: D

Ta có: $\hat{B A C} = \frac{1}{2} \hat{B O C} = \frac{1}{2} \cdot 120 ° = 60 °$ (góc nội tiếp và góc ở tâm cùng chắn cung BC).

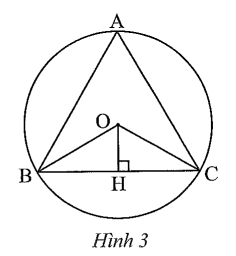
Câu 3 trang 98 sách bài tập Toán 9 Tập 1: Cho biết $sđ \overset{⏜}{A B} = sđ \overset{⏜}{B C} = sđ \overset{⏜}{C A}$ và OB = R. Độ dài cạnh BC là

Cho biết sđ cung AB = sđ cung BC = sđ cung CA và OB = R. Độ dài cạnh BC là

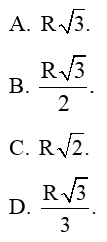
Lời giải:

Đáp án đúng là: A

Ta có: $sđ \overset{⏜}{A B} + sđ \overset{⏜}{B C} + sđ \overset{⏜}{C A} = 360 °$

Suy ra $3 \cdot sđ \overset{⏜}{B C} = 360 °$ nên $sđ \overset{⏜}{B C} = 120 °,$ hay $\hat{B O C} = 120 ° .$

Xét ∆OBC cân tại O (do OB = OC) nên đường cao OH đồng thời là đường trung tuyến và đường phân giác của tam giác, do đó BC = 2BH và $\hat{B O H} = \frac{1}{2} \hat{B O C} = \frac{1}{2} \cdot 120 ° = 60 ° .$

Xét ∆OBH vuông tại H, ta có:

$B H = O B \cdot \sin \hat{B O H} = R \cdot \sin 60 ° = \frac{R \sqrt{3}}{2} .$

Như vậy, $B C = 2 B H = 2 \cdot \frac{R \sqrt{3}}{2} = R \sqrt{3} .$

Câu 4 trang 99 sách bài tập Toán 9 Tập 1: Cho biết DE là tiếp tuyến của đường tròn trong Hình 4.

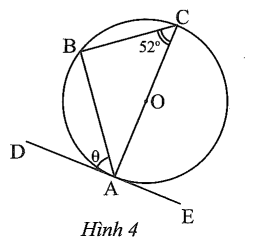
Cho biết DE là tiếp tuyến của đường tròn trong Hình 4. Số đo θ của góc BAD trong hình là

Số đo θ của góc $\hat{B A D}$ trong hình là

A. 28°.

B. 52°.

C. 56°.

D. 26°.

Lời giải:

Đáp án đúng là: B

Vì DE là tiếp tuyến của đường tròn (O) nên DE ⊥ OA tại A, suy ra $\hat{D A O} = 90 ° .$

Do đó $\hat{D A B} + \hat{B A O} = 90 °$ hay $\hat{D A B} = 90 ° - \hat{B A O} . (1)$

Xét ∆OAB cân tại O (do OA = OB) có:

$\hat{B A O} = \frac{180 ° - \hat{A O B}}{2} = 90 ° - \frac{1}{2} \hat{A O B} .$

Mà $\hat{A C B} = \frac{1}{2} \hat{A O B}$ (góc nội tiếp và góc ở tâm cùng chắn cung AB của đường tròn (O)).

Do đó $\hat{B A O} = 90 ° - \hat{A C B}$ hay $\hat{A C B} = 90 ° - \hat{B A O} . (2)$ >

Từ (1) và (2) suy ra $θ = \hat{D A B} = \hat{A C B} = 52 ° .$

Câu 5 trang 99 sách bài tập Toán 9 Tập 1: Cho biết DE là tiếp tuyến của đường tròn trong Hình 5.

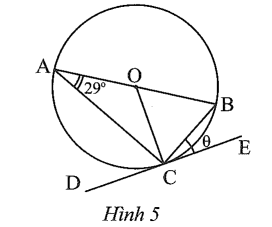
Cho biết DE là tiếp tuyến của đường tròn trong Hình 5. Số đo θ của góc BCE trong hình là

Số đo θ của góc $\hat{B C E}$ trong hình là

A. 29°.

B. 61°.

C. 58°.

D. 32°.

Lời giải:

Đáp án đúng là: A

Chứng minh tương tự Câu 4, trang 99, SBT Toán 9 Tập một, ta có:

$\hat{B C E} = \hat{B A C} = 29 ° .$

Câu 6 trang 99 sách bài tập Toán 9 Tập 1: Số đo θ của $\hat{R B S}$ có trong Hình 6 là

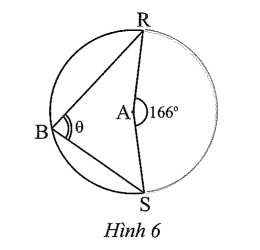
Số đo θ của góc RSB có trong Hình 6 là trang 99 sách bài tập Toán 9 Tập 1

A. 83°.

B. 41,5°.

C. 34°.

D. 66°.

Lời giải:

Đáp án đúng là: A

Ta có: $\hat{R B S} = \frac{1}{2} \hat{R A S}$ (góc nội tiếp và góc ở tâm cùng chắn cung RS của đường tròn (A)).

Suy ra $θ = \hat{R B S} = \frac{1}{2} \hat{R A S} = \frac{1}{2} \cdot 166 ° = 83 ° .$

Câu 7 trang 99 sách bài tập Toán 9 Tập 1: Cung 50° của một đường tròn đường kính d = 25 cm có độ dài (lấy π theo máy tính và kết quả làm tròn đến hàng phần trăm) là

A. 43,64 cm.

B. 10,91 cm.

C. 21,82 cm.

D. 87,28 cm.

Lời giải:

Đáp án đúng là: B

Bán kính của đường tròn là: $R = \frac{d}{2} = \frac{25}{2} = 12, 5 (cm).$

Độ dài của cung 50°, bán kính 12,5 cm là:

$l = \frac{π \cdot 12, 5 \cdot 50}{180} = \frac{125 π}{36} \approx 10, 91 (cm).$

Câu 8 trang 99 sách bài tập Toán 9 Tập 1: Hình quạt tròn bán kính R = 100 cm ứng với cung 40° có diện tích (lấy π theo máy tính và kết quả làm tròn đến hàng phần trăm) là

A. 34,91 cm².

B. 3 490,66 cm².

C. 69,82 cm².

D. 6 981,32 cm².

Lời giải:

Đáp án đúng là: B

Diện tích hình quạt tròn bán kính R = 100 cm ứng với cung 40° là:

$S = \frac{π \cdot 100^{2} \cdot 40}{360} = \frac{10 000 π}{9} \approx 3 490, 66 {(cm}^{2}).$

Câu 9 trang 99 sách bài tập Toán 9 Tập 1: Hình vành khuyên giới hạn bởi hai đường tròn (O; 5 cm) và (O; 2 cm) có diện tích (lấy π theo máy tính và kết quả làm tròn đến hàng phần trăm) là

A. 131,94 cm².

B. 18,84 cm².

C. 9,42 cm².

D. 65,97 cm².

Lời giải:

Đáp án đúng là: D

Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 5 cm) và (O; 2 cm) là:

S = π(5² – 2²) = 21π ≈ 65,97 (cm²).

Trong các câu từ 10 đến 12, chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Câu 10 trang 100 sách bài tập Toán 9 Tập 1: Chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Cho hai đường tròn C(O; 7 cm), C’(O’; 8 cm) và OO’ = 15 cm.

a) Hai đường tròn (C) và (C’) cắt nhau.

b) Hai đường tròn (C) và (C’) tiếp xúc ngoài.

c) Hai đường tròn (C) và (C’) tiếp xúc trong.

d) Hai đường tròn (C) và (C’) chỉ có một điểm chung duy nhất.

Lời giải:

Ta có: R = 7 cm; R’ = 8 cm; OO’ = 15 cm.

R’ + R = 8 + 7 = 15 = OO’.

Do đó hai đường tròn (O) và (O’) tiếp xúc ngoài nên hai đường tròn có một điểm chung duy nhất.

Vậy:

a) S.

b) Đ.

c) S.

d) Ð.

Câu 11 trang 100 sách bài tập Toán 9 Tập 1: Chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Cho bốn điểm A, B, C, D trên đường tròn (O) như Hình 7.

Chọn đúng hoặc sai cho mỗi ý a), b), c), d). Cho bốn điểm A, B, C, D trên đường tròn (O) như Hình 7

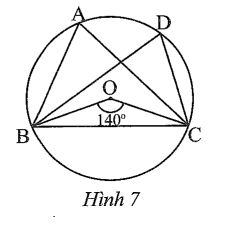
a) $\hat{B O C}$ là góc nội tiếp chắn cung $\overset{⏜}{B C}$ của đường tròn (O).

b) $\hat{O B C} = 40 ° .$

c) $\hat{B A C} = \hat{B D C} .$

d) $\hat{B A C} = 70 ° .$

Lời giải:

Xét đường tròn (O), ta có: $\hat{B O C}$ là góc ở tâm chắn cung $\overset{⏜}{B C};$ $\hat{B A C}, \hat{B D C}$ là hai góc nội tiếp chắn cung $\overset{⏜}{B C};$

Do đó $\hat{B A C} = \hat{B D C} = \frac{1}{2} \hat{B O C} = \frac{1}{2} \cdot 140 ° = 70 ° .$

Xét ∆OBC cân tại O (do OB = OC) nên

$\hat{O B C} = \hat{O C B} = \frac{180 ° - \hat{B O C}}{2} = \frac{180 ° - 140 °}{2} = 20 ° .$

Vậy:

a) S.

b) S.

c) Đ.

d) Đ.

Câu 12 trang 100 sách bài tập Toán 9 Tập 1: Chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Cho AB và AC là hai tiếp tuyến tiếp xúc với đường tròn (O; R) lần lượt tại hai tiếp điểm B và C (Hình 8).

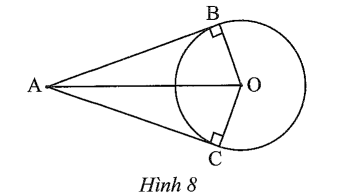
Chọn đúng hoặc sai cho mỗi ý a), b), c), d). Cho AB và AC là hai tiếp tuyến tiếp xúc với đường tròn (O; R)

a) AB = AO.

b) Tia AO là tia phân giác của $\hat{B A C} .$

c) Tia OA là tia phân giác của $\hat{B O C} .$

d) OA = OB = R.

Lời giải:

Do AB và AC là hai tiếp tuyến của đường tròn (O; R) lần lượt tại hai tiếp điểm B, C và chúng cắt nhau tại A nên:

⦁ OB = OC = R;

⦁ AB = AC;

⦁ Tia AO là tia phân giác của $\hat{B A C};$

⦁ Tia OA là tia phân giác của $\hat{B O C} .$

Vậy:

a) S.

b) Ð.

c) Ð.

d) S.

BÀI TẬP TỰ LUẬN

Bài 13 trang 100 sách bài tập Toán 9 Tập 1: Cho tam giác ABC nhọn với các đường cao AA’, BB’, CC’. Chứng minh rằng A’A là tia phân giác của góc

Lời giải:

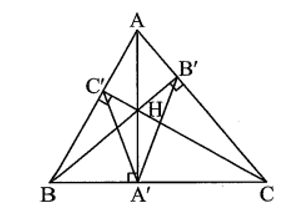
Gọi H là trực tâm của tam giác ABC.

Do AA’, BB’, CC’ là đường cao ∆ABC nên AA’ ⊥ BC; BB’ ⊥ AC; CC’ ⊥ AB.

Ta có:  nên bốn điểm B, A’, H, C’ cùng nằm trên đường tròn đường kính BH.

Do đó  (hai góc nội tiếp cùng chắn cung C’H).

Chứng minh tương tự, ta cũng có

Mà   (cùng phụ với > nên ta có

Vậy A’A là tia phân giác của góc
Bài 14 trang 100 sách bài tập Toán 9 Tập 1: Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (D thuộc cung nhỏ AB). Vẽ đường kính DE. Chứng minh rằng:

a) MA.MB = MC.MD.

b) Tứ giác ABEC là hình thang cân.

c) Tổng MA² + MB² + MC² + MD² có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O).

Lời giải:

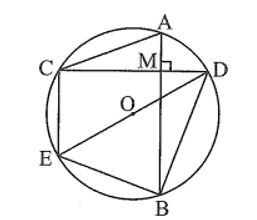
Do AB ⊥ CD nên $\hat{A M C} = \hat{D M B} = 90 ° .$

a) Xét đường tròn (O) có $\hat{A C D} = \hat{A B D}$ (hai góc nội tiếp cùng chắn cung AD).

Xét ∆MAC và ∆MDB, có:

$\hat{A M C} = \hat{D M B} = 90 °, \hat{A C M} = \hat{D B M}$

Do đó ∆MAC ᔕ ∆MDB (g.g).

Suy ra $\frac{M A}{M D} = \frac{M C}{M B}$ hay MA.MB = MC.MD.

b) Vì DE là đường kính của đường tròn (O) nên $\hat{E C D} = \hat{E B D} = 90 ° .$

Suy ra CE ⊥ CD.

Mà AB ⊥ CD nên AB // CE, do đó tứ giác ABEC là hình thang.

Mặt khác, $\hat{C A B} + \hat{A C M} = 90 °$ (tổng hai góc nhọn trong ∆ACM vuông tại M);

$\hat{E B A} + \hat{M B D} = \hat{E B D} = 90 °;$

$\hat{A C M} = \hat{D B M}$

Suy ra $\hat{E B A} = \hat{C A B} .$

Hình thang ABEC có $\hat{E B A} = \hat{C A B}$ nên ABEC là hình thang cân.

c) Xét ∆ACM vuông tại M, theo định lí Pythagore, ta có:

AC² = MA² + MC².

Xét ∆BDM vuông tại M, theo định lí Pythagore, ta có:

BD² = MB² + MD².

Do đó MA² + MB² + MC² + MD² = AC² + BD².

Lại có AC = BE (vì ABEC là hình thang cân) nên:

MA² + MB² + MC² + MD² = AC² + BD² = BE² + BD².

Xét ∆BDE vuông tại B, theo định lí Pythagore, ta có:

DE² = BD² + BE².

Do đó MA² + MB² + MC² + MD² = BE² + BD² = DE² = (2R)² = 4R², đây là giá trị không đổi do R không đổi.ở

Vậy tổng MA² + MB² + MC² + MD² có giá trị không đổi.
Bài 15 trang 100 sách bài tập Toán 9 Tập 1: Cho tam giác ABC cân tại A, $\hat{A} < 90 ° .$ Vẽ đường tròn đường kính AB cắt BC và AC lần lượt tại D và E. Chứng minh rằng:

a) ∆DBE là tam giác cân.

b) $\hat{C B E} = \frac{1}{2} \hat{B A C} .$

Lời giải:

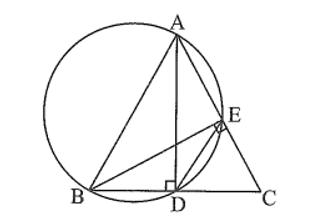
a) Ta có D, E cùng nằm trên đường tròn đường kính AB nên $\hat{A D B} = \hat{A E B} = 90 °$ hay AD ⊥ BC và BE ⊥ AC.

Xét ∆ABC cân tại A có AD là đường cao nên đồng thời là đường trung tuyến của tam giác, do đó D là trung điểm BC, suy ra $D B = D C = \frac{1}{2} B C .$

Xét ∆BEC vuông tại E có ED là đường trung tuyến ứng với cạnh huyền BC nên $E D = \frac{1}{2} B C .$

Do đó DE = DB = DC.

Vậy ∆BDE cân tại D.

b) Xét ∆ABC cân tại A có AD là đường cao nên đồng thời là tia phân giác của $\hat{B A C},$   do đó $\hat{B A D} = \frac{1}{2} \hat{B A C} .$

Ta có $\hat{D B E} = \hat{D E B}$ (do ∆BDE cân tại D) và $\hat{B A D} = \hat{B E D}$   (hai góc nội tiếp cùng chắn cung BD).

Suy ra $\hat{D B E} = \frac{1}{2} \hat{B A C}$   hay $\hat{C B E} = \frac{1}{2} \hat{B A C} .$
Bài 16 trang 101 sách bài tập Toán 9 Tập 1: Trong Hình 9, cho biết AB = 12, AC = 16; đường tròn (I) tiếp xúc với AH, BC và đường tròn (O); đường tròn (J) tiếp xúc với AH, BC và đường tròn (O).

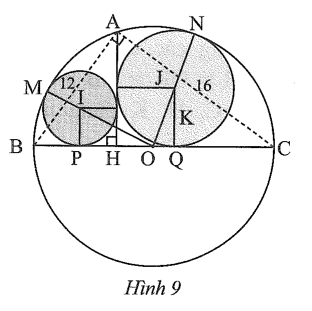
Tính:

a) BC, BH.

b) Bán kính R, R’ của đường tròn (I) và (J).

c) Khoảng cách PQ.

Lời giải:

a) Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:

$B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{12^{2} + 16^{2}} = \sqrt{400} = 20.$

Xét ∆BHA và ∆BAC có:

$\hat{B}$ là góc chung; $\hat{B H A} = \hat{B A C} = 90 ° .$

Do đó ∆BHA ᔕ ∆BAC (g.g), suy ra $\frac{B A}{B C} = \frac{B H}{B A}$

Nên $B H = \frac{B A^{2}}{B C} = \frac{12^{2}}{20} = \frac{144}{20} = 7, 2.$

b) Ta có $O B = O C = \frac{1}{2} B C = \frac{1}{2} \cdot 20 = 10;$

              OH = OB – BH = 10 – 7,2 = 2,8.

Gọi D là tiếp điểm của đường tròn (I) với AH.

Theo bài, đường tròn (I) tiếp xúc với AH, BC nên ID ⊥ AH và IP ⊥ BC.

Tứ giác IPHD có $\hat{I P H} = \hat{I D H} = \hat{P H D} = 90 °$ và ID = IP nên IPHD là hình vuông.

Do đó PH = IP = R.

Chứng minh tương tự, ta cũng có HQ = IQ = R’.

Áp dụng định lí Pythagore cho tam giác IPO vuông tại P, ta có:

IO² = IP² + PO²

Suy ra (OM – IM)² = IP² + (OH + PH)²

(10 – R)² = R² + (R + 2,8)²

100 – 20R + R² = R² + R² + 5,6R + 7,84

R² + 25,6R – 92,16 = 0

Phương trình trên có ∆ = 25,6² – 4.1.(–92,16) = 1 024 > 0 và $\sqrt{Δ} = \sqrt{1 024} = 32.$

Do đó phương trình trên có hai nghiệm là:

$R = \frac{- 25, 6 + 32}{2} = 3, 2$ (thỏa mãn);

$R = \frac{- 25, 6 - 32}{2} = - 28, 8$ (không thỏa mãn).

Áp dụng định lí Pythagore cho tam giác JQO vuông tại Q, ta có:

JO² = JQ² + QO²

Suy ra (ON – JN)² = R² + (HQ – OH)²

           (10 – R’)² = R’² + (R’ – 2,8)²

           100 – 20R’ + R’² = R’² + R’² – 5,6R’ + 7,84

           R’² + 14,4R – 92,16 = 0.

Phương trình trên có ∆ = 14,4² – 4.1.(–92,16) = 576 > 0 và $\sqrt{Δ} = \sqrt{576} = 24.$

Do đó phương trình trên có hai nghiệm là:

$R = \frac{- 14, 4 + 24}{2} = 4, 8$ (thỏa mãn);

$R = \frac{- 14, 4 - 24}{2} = - 19, 2$ (không thỏa mãn).

c) Ta có PQ = PH + QH = R + R’ = 3,2 + 4,8 = 8.
Bài 17 trang 101 sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại hai điểm A và B phân biệt. Vẽ đường thẳng vuông góc với AB tại A và cắt (O), (O’) lần lượt tại C, D. Tia CB cắt (O’) tại E, tia DB cắt (O) tại F. Chứng minh rằng:

a) CD.CA = CB.CE.

b) DC.DA = DB.DF.

c) CD² = CB.CE + DB.DF.

Lời giải:

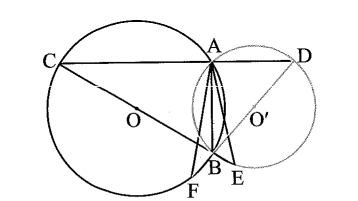
a) Trong đường tròn (O’), ta có:

⦁ $\hat{C D B} = \hat{A D B} = \frac{1}{2} sđ \overset{⏜}{A B}$ (góc nội tiếp chắn cung AB);

⦁ $\hat{C E A} = \hat{B E A} = \frac{1}{2} sđ \overset{⏜}{A B}$ (góc nội tiếp chắn cung AB).

Suy ra $\hat{C D B} = \hat{C E A} .$

Xét ∆CDB và ∆CEA có:

Góc C chung; $\hat{C D B} = \hat{C E A} .$

Do đó ∆CDB ᔕ ∆CEA (g.g)

Suy ra $\frac{C D}{C E} = \frac{C B}{C A}$ hay CD.CA = CB.CE.

b) Xét đường tròn (O) có $\hat{D C B} = \hat{A F B} = \hat{A F D}$ (hai góc nội tiếp chắn dây cung AB)

Xét ∆CDB và ∆FDA có:

Góc D chung; $\hat{D C B} = \hat{A F D}$

Do đó ∆CDB ᔕ ∆FDA (g.g)

Suy ra $\frac{C D}{F D} = \frac{B D}{D A}$ hay DC.DA = DB.DF.

c) Ta có:

CB.CE + DB.DF = CD.CA + DC.DA = CD(CA + AD) = CD.CD = CD².

Vậy CB.CE + DB.DF = CD².

Bài 18 trang 101 sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R’) (R > R’) tiếp xúc trong tại A. Một tiếp tuyến của đường tròn (O’) tại M cắt đường tròn (O) tại hai điểm B, C. Đường thẳng BO’ cắt đường tròn (O) tại điểm thứ hai D và cắt đường thẳng AM tại E. Gọi F là giao điểm thứ hai của đường tròn ngoại tiếp tam giác ADE với AC và N là giao điểm thứ hai của AN với (O). Chứng minh rằng:

a) O’M // ON.

b) Ba điểm D, N, F thẳng hàng.

c) DF là tia phân giác của góc $\hat{B D C} .$

Lời giải:

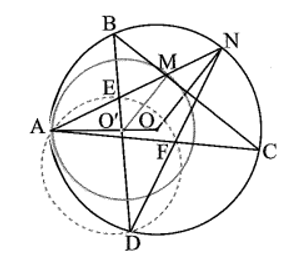
Cho hai đường tròn (O; R) và (O’; R’) (R > R’) tiếp xúc trong tại A. Một tiếp tuyến của đường tròn (O’) tại M

a) Xét ∆O’AM cân tại O’ (do O’A = O’M) nên $\hat{O^{'} A M} = \hat{O' M A} .$

Xét ∆OAN cân tại O (do OA = ON) nên $\hat{O A N} = \hat{A N O} .$

Do đó $\hat{O' M A} = \hat{O N A},$ mà hai góc này ở vị trí đồng vị, suy ra O’M // ON.

b) Do BC là tiếp tuyến của (O’) nên O’M ⊥ BC.

Mà O’M // ON nên ON ⊥ BC.

Xét ∆OBC cân tại O (do OB = OC) nên đường cao ON đồng thời là đường phân giác của tam giác, hay $\hat{B O N} = \hat{C O N},$ do đó $sđ \overset{⏜}{B N} = sđ \overset{⏜}{N C}$ hay N là điểm chính giữa cung BC.

Mặt khác $\hat{N A C} = \hat{N D C} = \frac{1}{2} sđ \overset{⏜}{N C}$ (hai góc nội tiếp cùng chắn cung NC của đường tròn (O)) và $\hat{B D N} = \frac{1}{2} sđ \overset{⏜}{B N}$ (góc nội tiếp chắn cung BN của đường tròn (O))

Do đó $\hat{B D N} = \hat{N A C} = \hat{E A F} .$ (1)

Trong đường tròn ngoại tiếp tam giác ADE, ta có:

$\hat{E A F} = \hat{E D F} = \hat{B D F}$ (góc nội tiếp cùng chắn cung EF). (2)

Từ (1), (2) ta có $\hat{B D F} = \hat{B D N},$ suy ra D, N, F thẳng hàng.

c) Ta có hai cung BN và NC có số đo bằng nhau, suy ra $\hat{B D N} = \hat{N D C}$ (hai góc nội tiếp chắn hai cung bằng nhau) hay DF là tia phân giác của $\hat{B D C} .$