Với giải HĐ1 trang 13 Toán 12 Tập 2 Kết nối tri thức chi tiết trong Bài 12: Tích phân giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài 12: Tích phân

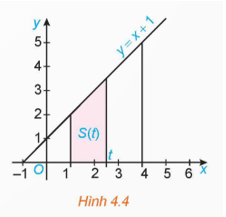
HĐ1 trang 13 Toán 12 Tập 2: Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y = x + 1, trục hoành và hai đường thẳng x = 1, x = t (1 ≤ t ≤ 4) (H.4.4)

a) Tính diện tích S của T khi t = 4.

b) Tính diện tích S(t) của T khi t ∈ [1; 4].

c) Chứng minh rằng S(t) là một nguyên hàm của hàm số f(t) = t + 1, t ∈ [1; 4] và diện tích S = S(4) – S(1).

Lời giải:

a)

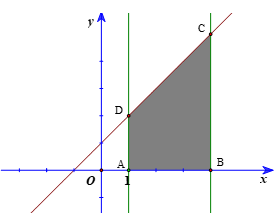
Kí hiệu A(1; 0), B(4; 0) và C, D lần lượt là giao điểm của đường thẳng x = 4; x = 1 với đường thẳng y = x + 1.

Khi đó C(4; 5), D(1; 2).

Ta có: AD = 2; BC = 5; AB = 3.

Khi đó diện tích hình thang T là $S=\frac{\left(AD+BC\right).AB}{2}=\frac{\left(2+5\right).3}{2}=\frac{21}{2}$.

b)

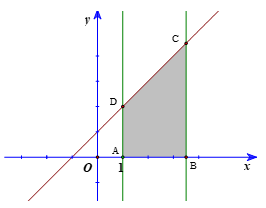
Gọi A(1; 0), B(t; 0), t ∈ [1; 4] và C, D lần lượt là giao điểm của đường thẳng x = t; x = 1 với đường thẳng y = x + 1.

Khi đó C(t; t + 1); D(1; 2).

Do đó AB = t – 1; AD = 2; BC = t + 1.

Khi đó diện tích hình thang ABCD là

$S\left(t\right)=\frac{\left(AD+BC\right).AB}{2}=\frac{\left(t+3\right).\left(t-1\right)}{2}=\frac{t^2+2t-3}{2}.$

c) Có $S\left(t\right)=\frac{t^2+2t-3}{2}$$\Rightarrow S^{\text{'}}\left(t\right)={\left(\frac{t^2+2t-3}{2}\right)}^{\text{'}}=\frac{2\left(t+1\right)}{2}=t+1=f\left(t\right)$

Do đó S(t) là một nguyên hàm của hàm số f(t) = t + 1, t ∈ [1; 4].

Có $S\left(4\right)=\frac{4^2+2.4-3}{2}=\frac{21}{2};S\left(1\right)=\frac{1^2+2.1-3}{2}=0$

Do đó S(4) – S(1) = S.