Với tóm tắt lý thuyết Toán lớp 12 Bài 3: Đường tiệm cận của đồ thị hàm số sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số

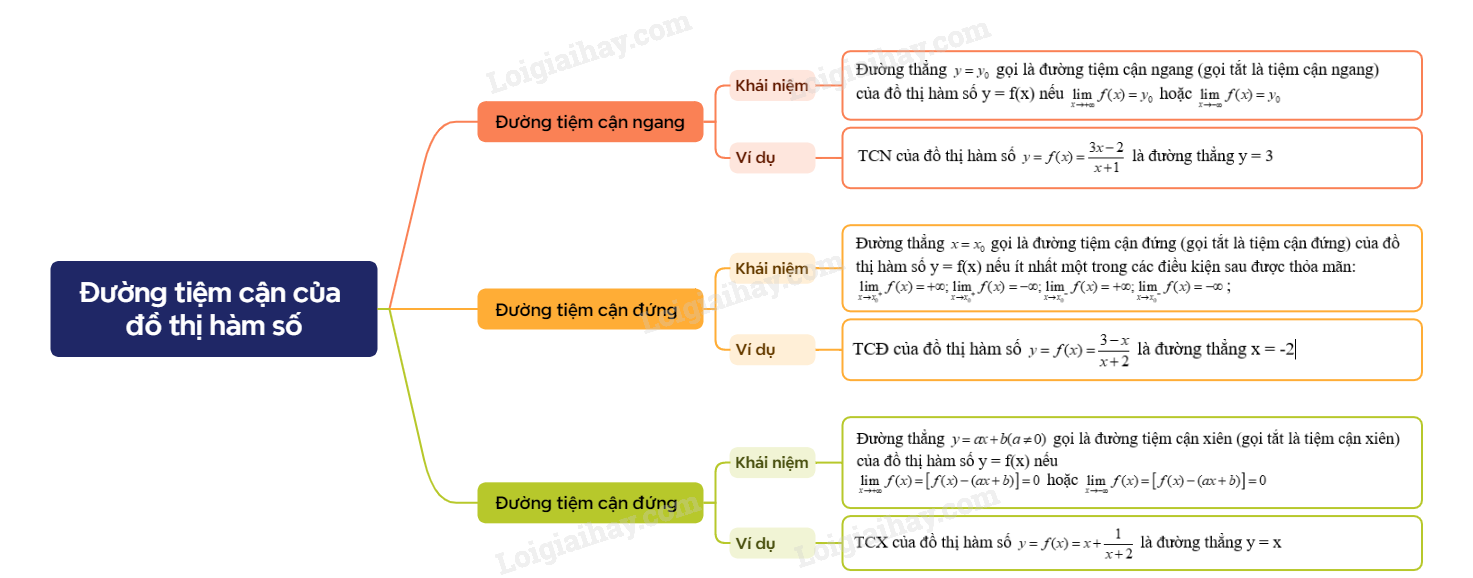
A. Lý thuyết Đường tiệm cận của đồ thị hàm số

1. Đường tiệm cận ngang

Ví dụ: Tìm TCN của đồ thị hàm số $y=f(x)=\frac{3x-2}{x+1}$

Ta có: $\underset{x\to +\mathrm{\infty }}{lim}\frac{3x-2}{x+1}=\underset{x\to -\mathrm{\infty }}{lim}\frac{3x-2}{x+1}=3$

Vậy đồ thị hàm số f(x) có TCN là y = 3.

2. Đường tiệm cận đứng

Ví dụ: Tìm TCĐ của đồ thị hàm số $y=f(x)=\frac{3-x}{x+2}$

Ta có: $\underset{x\to -2^{+}}{lim}\frac{3x-2}{x+2}=+\mathrm{\infty }$

Vậy đồ thị hàm số có TCĐ là x = -2

3. Đường tiệm cận xiên

Ví dụ: Tìm TCX của đồ thị hàm số $y=f(x)=x+\frac{1}{x+2}$

Ta có: $\underset{x\to +\mathrm{\infty }}{lim}\left[f(x)-x\right]=\underset{x\to +\mathrm{\infty }}{lim}\frac{1}{x+2}=0$

Vậy đồ thị hàm số có TCX là y = x

Sơ đồ tư duy Đường tiệm cận của đồ thị hàm số

B. Bài tập Đường tiệm cận của đồ thị hàm số

Bài 1. Đồ thị hàm số $y=\frac{1-3x}{x+2}$ có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:

A. x = −2 và y = −3.   

B. x = −2 và y = 1.

C. x = −2 và y = 3.  

D. x = 2 và y = 1.

Hướng dẫn giải

Đáp án đúng là: A

Có $\underset{x\to {\left(-2\right)}^{+}}{\lim }y=\underset{x\to {\left(-2\right)}^{+}}{\lim }\frac{1-3x}{x+2}=+\infty ;\underset{x\to {\left(-2\right)}^{-}}{\lim }y=\underset{x\to {\left(-2\right)}^{-}}{\lim }\frac{1-3x}{x+2}=-\infty$

Do đó x = −2 là tiệm cận đứng của đồ thị hàm số.

Có $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{1-3x}{x+2}=-3;\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{1-3x}{x+2}=-3$.

Do đó y = −3 là tiệm cận ngang của đồ thị hàm số.

Bài 2. Cho hàm số y = f(x) có bảng biến thiên như sau

Trong các mệnh đề sau về hàm số y = f(x), mệnh đề nào đúng?

A. Đồ thị hàm số có tiệm cận đứng x = 1.

B. Hàm số nghịch biến trên ℝ.

C. Hàm số đồng biến trên ℝ.

D. Hàm số có một điểm cực trị.

Hướng dẫn giải

Đáp án đúng là: A

Dựa vào bảng biến thiên, ta có:

+) Hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).

+) Hàm số không có cực trị

+) Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số và đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.

Bài 3. Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\frac{2x+1}{x+1}$.

Hướng dẫn giải

Tập xác định: D = ℝ\{−1}.

$\underset{x\to {\left(-1\right)}^{-}}{\lim }y=\underset{x\to {\left(-1\right)}^{-}}{\lim }\frac{2x+1}{x+1}=+\infty ;\underset{x\to {\left(-1\right)}^{+}}{\lim }y=\underset{x\to {\left(-1\right)}^{+}}{\lim }\frac{2x+1}{x+1}=-\infty$

Do đó đường thẳng x = −1 là tiệm cận đứng của đồ thị hàm số.

$\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{2x+1}{x+1}=2;\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{2x+1}{x+1}=2$.

Do đó đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.

Bài 4. Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số $y=\frac{x^2+x+1}{x+1}$.

Hướng dẫn giải

Tập xác định: D = ℝ\{−1}.

Có $\underset{x\to {\left(-1\right)}^{+}}{\lim }y=\underset{x\to {\left(-1\right)}^{+}}{\lim }\frac{x^2+x+1}{x+1}=+\infty ;\underset{x\to {\left(-1\right)}^{-}}{\lim }y=\underset{x\to {\left(-1\right)}^{-}}{\lim }\frac{x^2+x+1}{x+1}=-\infty$

Do đó đường thẳng x = −1 là tiệm cận đứng của đồ thị hàm số.

Có $y=\frac{x^2+x+1}{x+1}=x+\frac{1}{x+1}$.

Có $\underset{x\to +\infty }{\lim }\left(y-x\right)=\underset{x\to +\infty }{\lim }\left(x+\frac{1}{x+1}-x\right)=\underset{x\to +\infty }{\lim }\frac{1}{x+1}=0;$

$\underset{x\to -\infty }{\lim }\left(y-x\right)=\underset{x\to -\infty }{\lim }\left(x+\frac{1}{x+1}-x\right)=\underset{x\to -\infty }{\lim }\frac{1}{x+1}=0$.

Do đó đường thẳng y = x là tiệm cận xiên của đồ thị hàm số.

Bài 5. Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức $f\left(t\right)=\frac{26t+10}{t+5}$ (f(t) được tính bằng nghìn người).

Xem y = f(t) là một hàm số xác định trên nửa khoảng [0; +∞). Hãy tìm các đường tiệm cận của đồ thị hàm số.

Hướng dẫn giải

Ta có $\underset{t\to +\infty }{\lim }f\left(t\right)=\underset{t\to +\infty }{\lim }\frac{26t+10}{t+5}=\underset{t\to +\infty }{\lim }\frac{26+\frac{10}{t}}{1+\frac{5}{t}}=26$ .

Do đó y = 26 là tiệm cận ngang của đồ thị hàm số.

Trên nửa khoảng [0; +∞) đồ thị hàm số không có tiệm cận đứng.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 12 Kết nối tri thức hay, chi tiết khác: