Lý thuyết Vectơ trong không gian (Kết nối tri thức 2024)

Lý thuyết Vectơ trong không gian (Kết nối tri thức 2024) | Lý thuyết Toán 12

Admin Vietjack Ngày: 05-08-2024 Lớp 12

1.9 K

Với tóm tắt lý thuyết Toán lớp 12 Bài 6: Vectơ trong không gian sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán 12 Bài 6: Vectơ trong không gian

A. Lý thuyết Vectơ trong không gian

1. Vecto trong không gian

Khái niệm vecto trong không gian

- Vecto trong không gian là một đoạn thẳng có hướng

- Độ dài của vecto trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vecto đó

- Hai vecto được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau

- Nếu hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng

- Hai vecto $\vec{a}$ và $\vec{b}$ được gọi là bằng nhau, kí hiệu $\vec{a}$ = $\vec{b}$ , nếu chúng có cùng độ dài và cùng hướng

2. Tổng và hiệu của hai vecto trong không gian

a) Tổng của hai vecto trong không gian

Trong không gian, cho hai vecto $\vec{a}$ và $\vec{b}$ . Lấy một điểm A bất kì và các điểm B,C sao cho $\vec{A B} = \vec{a}, \vec{B C} = \vec{b}$ . Khi đó, vecto $\vec{A C}$ được gọi là tổng của hai vecto $\vec{a}$ và $\vec{b}$ , kí hiệu là $\vec{a} + \vec{b}$

Trong không gian, phép lấy tổng của hai vecto được gọi là phép cộng vecto

Quy tắc hình hộp

Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có $\vec{A B} + \vec{A D} + \vec{A A^{'}} = \vec{A C^{'}}$

b) Hiệu của hai vecto trong không gian

Trong không gian, vecto có cùng độ dài và ngược hướng với vecto $\vec{a}$ được gọi là vecto đối của vecto $\vec{a}$ , kí hiệu là - $\vec{a}$

Vecto $\vec{a} + (- \vec{b})$ được gọi là hiệu của hai vecto $\vec{a}$ và $\vec{b}$ và kí hiệu là $\vec{a} - \vec{b}$

Trong không gian, phép lấy hiệu của hai vecto được gọi là phép trừ vecto

3. Tích của một số với một vecto trong không gian

Trong không gian, tích của một số thực $k \neq 0$ với một vecto $\vec{a} \neq \vec{0}$ là một vecto, kí hiệu là $k \vec{a}$ , được xác định như sau:

- Cùng hướng với vecto $\vec{a}$ nếu k > 0; ngược hướng với vecto $\vec{a}$ nếu k < 0

- Có độ dài bằng $| k | . | \vec{a} |$

Trong không gian, phép lấy tích của một số với một vecto được gọi là phép nhân một số với một vecto

4. Tích vô hướng của hai vecto trong không gian

a) Góc giữa hai vecto trong không gian

Trong không gian, cho hai vecto $\vec{a}$ và $\vec{b}$ khác $\vec{0}$ . Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho $\vec{O A} = \vec{a}, \vec{O B} = \vec{b}$ . Khi đó, góc $\hat{A O B} (0^{\circ} \leq \hat{A O B} \leq 180^{\circ})$ được gọi là góc giữa hai vecto $\vec{a}$ và $\vec{b}$ , kí hiệu $(\vec{a}, \vec{b})$

b) Tích vô hướng của hai vecto trong không gian

Trong không gian, cho hai vecto $\vec{a}$ và $\vec{b}$ khác $\vec{0}$ . Tích vô hướng của hai vecto $\vec{a}$ và $\vec{b}$ là một số, kí hiệu là $\vec{a} \cdot \vec{b}$ , được xác định bởi công thức

$\vec{a} \cdot \vec{b} = | \vec{a} | \cdot | \vec{b} | \cdot \cos (\vec{a}, \vec{b})$

Sơ đồ tư duy Vectơ trong không gian

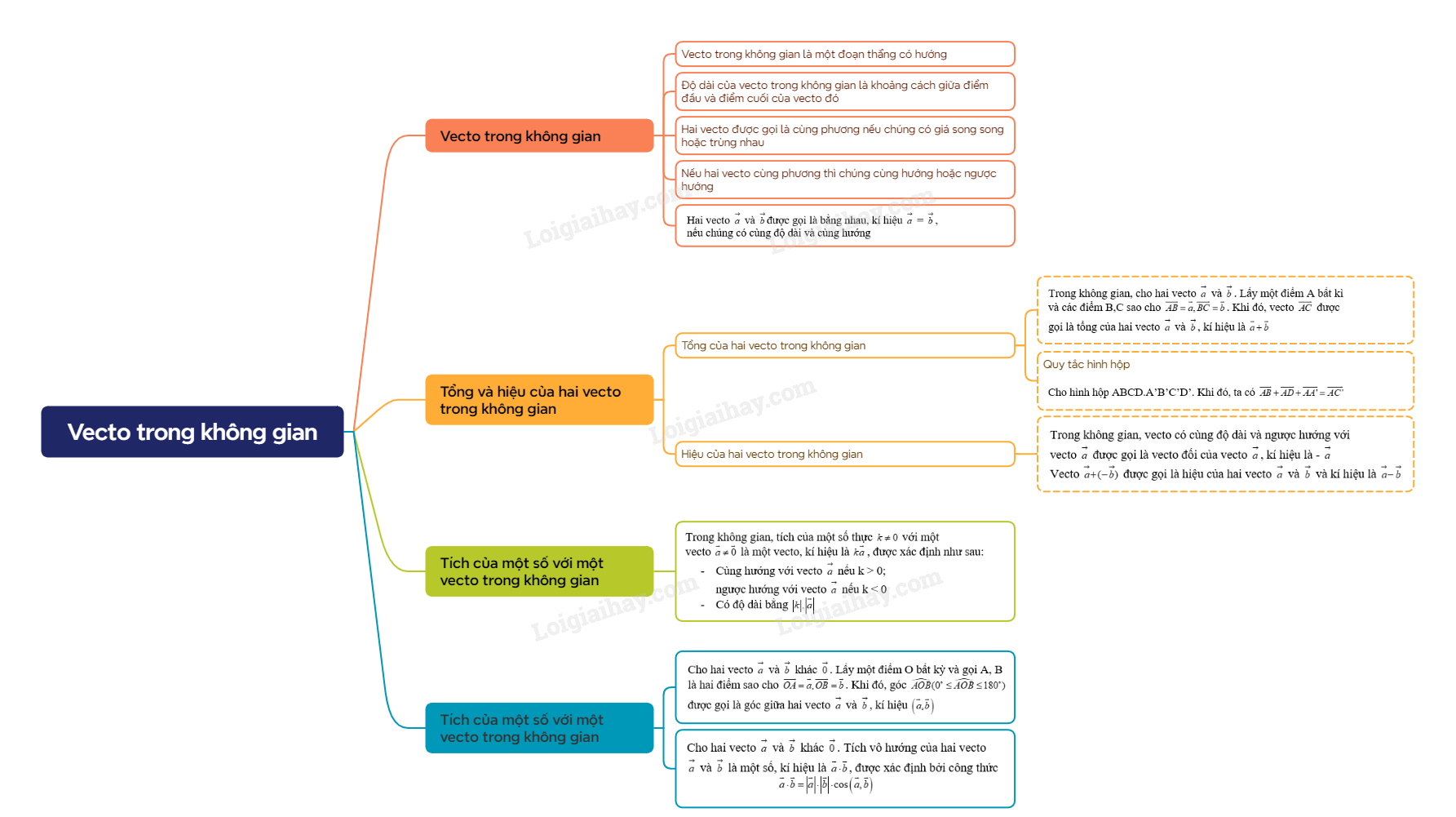
B. Bài tập Vectơ trong không gian

Bài 1. Cho tứ diện ABCD. Đặt $\vec{A B} = \vec{a}, \vec{A C} = \vec{b}, \vec{A D} = \vec{c}$ . Gọi G là trọng tâm tam giác BCD. Trong các đẳng thức sau, đẳng thức nào sau đây đúng?

A. $\vec{A G} = \vec{a} + \vec{b} + \vec{c}$ .

B. $\vec{A G} = \frac{1}{3} (\vec{a} + \vec{b} + \vec{c})$ .

C. $\vec{A G} = \frac{1}{2} (\vec{a} + \vec{b} + \vec{c})$ .

D. $\vec{A G} = \frac{1}{4} (\vec{a} + \vec{b} + \vec{c})$ .

Hướng dẫn giải

Đáp án đúng là: B

Vectơ trong không gian (Lý thuyết Toán lớp 12) | Kết nối tri thức

Gọi M là trung điểm của CD suy ra $\vec{B G} = \frac{2}{3} \vec{B M}$ .

Có $\vec{A G} = \vec{A B} + \vec{B G} = \vec{A B} + \frac{2}{3} \vec{B M} = \vec{A B} + \frac{2}{3} . \frac{1}{2} . (\vec{B C} + \vec{B D}) = \vec{A B} + \frac{1}{3} . (\vec{B C} + \vec{B D})$

Bài 2. Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ $\vec{A B}$ và $\vec{D H}$ .

A. 45°.

B. 90°.

C. 120°.

D. 60°.

Hướng dẫn giải

Đáp án đúng là: B

Vectơ trong không gian (Lý thuyết Toán lớp 12) | Kết nối tri thức

Do ADHE là hình vuông nên $\vec{A E} = \vec{D H}$ .

Do đó $(\vec{A B}, \vec{D H}) = (\vec{A B}, \vec{A E}) = \hat{B A E} = 90^{\circ}$ (do ABFE là hình vuông).

Bài 3. Cho các điểm $A, B, C, D, E, F$ . Chứng minh rằng

a) $\vec{A B} + \vec{D C} = \vec{A C} + \vec{D B}$ .

b) $\vec{A B} + \vec{C D} + \vec{E F} = \vec{A F} + \vec{E D} + \vec{C B}$ .

Hướng dẫn giải

a) Ta có: $V T = \vec{A C} + \vec{C B} + \vec{D B} + \vec{B C} = (\vec{A C} + \vec{D B}) + (\vec{B C} + \vec{C B})$ $= \vec{A C} + \vec{D B} = V P$ .

b) Biến đổi $V T = \vec{A F} + \vec{F B} + \vec{C B} + \vec{B D} + \vec{E D} + \vec{D F}$

$= (\vec{A F} + \vec{E D} + \vec{C B}) + (\vec{F B} + \vec{B D} + \vec{D F}) = \vec{A F} + \vec{E D} + \vec{C B} = V P$

Bài 4. Cho tứ diện ABCD có AB = AC = AD và $\hat{B A C} = \hat{B A D} = 60^{\circ}$ . Hãy xác định góc giữa cặp vectơ $\vec{A B}$ và $\vec{C D}$ .

Hướng dẫn giải

Vectơ trong không gian (Lý thuyết Toán lớp 12) | Kết nối tri thức

Ta có $\vec{A B} . \vec{C D} = \vec{A B} . (\vec{A D} - \vec{A C}) = \vec{A B} . \vec{A D} - \vec{A B} . \vec{A C}$ (1).

Mà $\vec{A B} . \vec{A D} = | \vec{A B} | . | \vec{A D} | . \cos \hat{B A D}$ (2).

$\vec{A B} . \vec{A C} = | \vec{A B} | . | \vec{A C} | . \cos \hat{B A C}$ (3).

AB = AC = AD và $\hat{B A C} = \hat{B A D} = 60^{\circ}$ (4).

Từ (1), (2), (3) và (4), ta có $\vec{A B} . \vec{C D} = 0 \Rightarrow (\vec{A B}, \vec{C D}) = 90^{\circ}$ .

Bài 5. Công của lực $\vec{F}$ làm một chất điểm chuyển động một đoạn đường $\vec{d}$ được tính bởi công thức $W = \vec{F} . \vec{d}$ . Hình vẽ sau mô tả một người đẩy chiếc xe di chuyển một đoạn 20 m với lực đẩy 50 N, góc đẩy là 60°. Tính công của lực đã nêu.