Với tóm tắt lý thuyết Toán lớp 12 Bài 1: Tính đơn điệu và cực trị của hàm số sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số

A. Lý thuyết Tính đơn điệu và cực trị của hàm số

1. Tính đơn điệu của hàm số

Khái niệm tính đơn điệu của hàm số

Ví dụ: Hàm số y = |x| đồng biến trên khoảng $\left(0;+\mathrm{\infty }\right)$, nghịch biến trên khoảng $\left(-\mathrm{\infty };0\right)$

Định lý

Ví dụ: Hàm số $y=x^2-4x+2$ có y’ = 2x – 4

• y’ > 0 với $x\in (2;+\mathrm{\infty })$ nên HS đồng biến trên khoảng $\left(2;+\mathrm{\infty }\right)$
• y’ < 0 với $x\in (-\mathrm{\infty };2)$ nên HS đồng biến trên khoảng $\left(-\mathrm{\infty };2\right)$

Sử dụng BBT xét tính đơn điệu của hàm số

Ví dụ: Xét chiều biến thiên của hàm số $y=\frac{x-2}{x+1}$

1. Tập xác định của hàm số là $R\mathrm{\setminus }\left\{-1\right\}$

2. Ta có: $y^{\prime }=\frac{(x+1)-(x-2)}{{(x+1)}^2}=\frac{3}{{(x+1)}^2}>0\mathrm{\forall }x\ne -1$

3. BBT

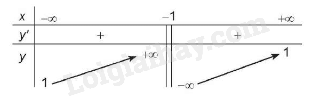
4. Hàm số đồng biến trên các khoảng $\left(-\mathrm{\infty };-1\right)$ và $\left(-1;+\mathrm{\infty }\right)$

2. Cực trị của hàm số

Khái niệm cực trị của hàm số

Ví dụ: Cho đồ thị của hàm số y = f(x) như sau

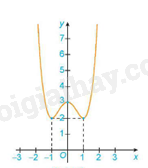
Hàm số đạt cực tiểu tại x = -1 và $y_{CT}$= y(-1) = 2

Hàm số đạt cực đại tại x = 0 và = y(0) = 3

Hàm số đạt cực tiểu tại x = 1 và $y_{CT}$= y(1) = 2

Cách tìm cực trị của hàm số

Ví dụ: Tìm cực trị của hàm số $y=x^3-6x^2+9x+30$.

Tập xác định của hàm số là R.

Ta có: $y^{\prime }=3x^2-12x+9$; y’ = 0 $\iff$x = 1 hoặc x = 3.

BBT:

Hàm số đạt cực đại tại x = 1 và = y(1) = 34

Hàm số đạt cực tiểu tại x = 3 và $y_{CT}$= y(3) = 30

B. Bài tập Tính đơn điệu và cực trị của hàm số

Bài 1. Cho hàm số y = x³ + 3x² – 9x + 15. Khẳng định nào sau đây là khẳng định sai?

A. Hàm số nghịch biến trên khoảng (−3; 1).

B. Hàm số đồng biến trên (−9; −5).

C. Hàm số đồng biến trên ℝ.

D. Hàm số đồng biến trên (5; +∞).

Hướng dẫn giải

Đáp án đúng là: C

Tập xác định: D = ℝ.

Có y' = 3x² + 6x – 9; y' = 0 $\iff$ x = −3 hoặc x = 1.

Bảng biến thiên:

Dựa vào bảng biến thiên, ta có:

Hàm số đồng biến trên cách khoảng (−∞; −3) và (1; +∞).

Hàm số nghịch biến trên khoảng (−3; 1).

Bài 2. Hàm số y = x⁴ – 2x² + 1 có bao nhiêu điểm cực trị?

A. 2.       

B. 3.       

C. 1.        

D. 0.

Hướng dẫn giải

Đáp án đúng là: B

Tập xác định: D = ℝ.

Có y' = 4x³ – 4x; y' = 0 $\iff$ x = −1 hoặc x = 0 hoặc x = 1.

Bảng biến thiên

Dựa vào bảng biến thiên, ta có:

Hàm số đạt cực tiểu tại x = ±1 và y_CT = 0.

Hàm số đạt cực đại tại x = 0 và y_CĐ = 1.

Bài 3. Tìm các khoảng đơn điệu của các hàm số sau

a) y = x³ – 3x;         

b) $y=\frac{2x-1}{x-1}$.

Hướng dẫn giải

a) Tập xác định: D = ℝ.

Có y' = 3x² – 3; y' = 0$\iff$x = 1 hoặc x = −1.

Bảng biến thiên

Dựa vào bảng biến thiên, ta có

Hàm số đồng biến trên các khoảng (−∞; −1) và (1; +∞).

Hàm số nghịch biến trên khoảng (−1; 1).

b) Tập xác định: D = ℝ\{1}.

Có $y\text{'}=\frac{2(x-1)-(2x-1)}{{(x-1)}^2}=\frac{-1}{{(x-1)}^2}<0,\forall x\ne 1$ .

Do đó hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).

Bài 4. Tìm cực trị của các hàm số sau

a) $y=\frac{2x+3}{x+1}$;     

b) y = 2x⁴ – 4x² + 2022.

Hướng dẫn giải

a) Tập xác định: D = ℝ\{−1}.

Có $y\text{'}=\frac{2(x+1)-(2x+3)}{{(x+1)}^2}=\frac{-1}{{(x+1)}^2}<0,\forall x\ne -1$.

Do đó hàm số không có cực trị.

b) Tập xác định: D = ℝ.

Có y' = 8x³ – 8x; y' = 0 $\iff$ x = −1 hoặc x = 0 hoặc x = 1.

Bảng biến thiên

Dựa vào bảng biến thiên ta có:

Hàm số đạt cực đại tại x = 0 và y_CĐ = 2022.

Hàm số đạt cực tiểu tại x = ±1 và y_CT = 2020.

Bài 5. Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức G(x) = 0,024x²(30 – x), trong đó x là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp (x được tính bằng mg). Tìm lượng thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.

Hướng dẫn giải

Tập xác định: D = (0; 30).

Có G'(x) = 0,048x(30 – x) – 0,024x² = 0,024x(60 – 3x);

G'(x) = 0 $\iff$ x = 0 hoặc x = 20.

Bảng biến thiên

Dựa vào bảng biến thiên, ta có lượng thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất là x = 20 mg.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 12 Kết nối tri thức hay, chi tiết khác: