Tailieumoi.vn xin giới thiệu Tìm m để hàm số đồng biến, nghịch biến trên khoảng cho trước được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 12. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Tìm m để hàm số đồng biến, nghịch biến trên khoảng cho trước. Mời các bạn đón xem:
Tìm m để hàm số đồng biến, nghịch biến trên khoảng cho trước
A. Lý thuyết Tìm m để hàm số đồng biến, nghịch biến trên khoảng cho trước
Lý thuyết cần nhớ: Cho hàm số y = f(x,m) có tập xác định D, khoảng (a;b)⊂D:
Hàm số nghịch biến trên (a;b) ⇔ y' ≤ 0, ∀ x ∈ (a;b)
Hàm số đồng biến trên (a;b) ⇔ y' ≥ 0, ∀ x ∈ (a;b)
Ghi nhớ: f'(x) = 0 chỉ tại một số điểm hữu hạn của K.
Chú ý: Riêng hàm số 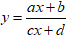
Hàm số nghịch biến trên (a;b) ⇔ y' < 0, ∀ x ∈ (a;b)
Hàm số đồng biến trên (a;b) ⇔ y' > 0, ∀ x ∈ (a;b)
Nếu gặp bài toán tìm m để hàm số đồng biến (hoặc nghịch biến) trên khoảng (a;b):
Bước 1: Đưa bất phương trình f'(x) ≥ 0 (hoặcf'(x) ≤ 0), ∀ x ∈ (a;b) về dạng g(x) ≥ h(m) (hoặc g(x) ≤ h(m)), ∀ x ∈ (a;b).
Bước 2: Lập bảng biến thiên của hàm số g(x) trên (a;b).
Bước 3: Từ bảng biến thiên và các điều kiện thích hợp ta suy ra các giá trị cần tìm của tham số m.
Dấu tam thức bậc hai
Cho tam thức g(x) = ax2 + bx + c (a ≠ 0)
Nếu hàm số f(x) có giá trị nhỏ nhất trên tập D, thế thì: 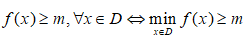
Nếu hàm số f(x) có giá trị lớn nhất trên tập D, thế thì: 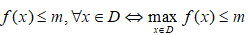
B. Bài tập ứng dụng
1. Bài tập trắc nghiệm
Bài 1: Tìm tất cả các giá trị m để hàm số 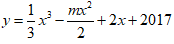
Lời giải:
Chọn A
TXĐ: D = R
Để hàm số y = f(x) đồng biến trên R ⇔ y' ≥ 0 với mọi x ∈ R
Bài 2: Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số 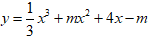
Lời giải:
Chọn C
TXĐ: D = R
Ta có: y' = x2 + 2mx + 4
Hàm số đồng biến trên R khi và chỉ khi y' ≥ 0, ∀ x ∈ R.
⇔ Δ' = m2-4 ≤ 0 ⇔ -2 ≤ m ≤ 2.
Bài 3: Tìm tất cả các giá trị của tham số m để hàm số 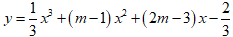
A. m > 2.
B. m ≤ 2.
C. m < 1.
D. m ≥ 1.
Lời giải:
Chọn D
TXĐ: D = R
Hàm số đồng biến trên khoảng (1;+∞) ⇔ y' ≥ 0; ∀ x ∈ (1;+∞)
Ta có y' = x2 + 2(m - 1)x + 2m - 3 = (x + 1)(x + 2m - 3) ≥ 0; ∀ x ∈ (1;+∞)
Do x > 1 nên (x + 1) > 0, nên (x + 2m - 3) ≥ 0 với mọi x > 1.
2m - 3 ≥ -x; ∀ x > 1 ⇔ 2m - 3 ≥ -1 ⇔ m ≥ 1.
Bài 4: Cho hàm số 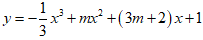
Lời giải:
Chọn C
TXĐ: D = R
Ta có y' = -x2 + 2mx + 3m + 2.
Hàm số nghịch biến trên R khi và chỉ khi y' ≤ 0, ∀ x ∈ R
Bài 5: Tất cả các giá trị thực của tham số m sao cho hàm số y = -x4 + (2m - 3)x2 + m nghịch biến trên khoảng (1;2) là 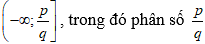
A. 5.
B. 9.
C. 7.
D. 3.
Lời giải:
Chọn C
Tập xác định D = R.
Ta có y' = -4x3 + 2(2m - 3)x.
Hàm số nghịch biến trên (1;2) ⇔ y' ≤ 0, ∀ x ∈ (1;2).
⇔ -4x3 + 2(2m - 3)x ≤ 0, ∀ x ∈ (1;2) ⇔ -4x2 + 4m - 6 ≤ 0, ∀ x ∈ (1;2) (do x > 0)
Lập bảng biến thiên của g(x) trên (1;2). g'(x) = 2x = 0 ⇔ x = 0
Bảng biến thiên
Vậy p + q = 5 + 2 = 7.
Bài 6: Tìm m để hàm số 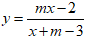
A. 1 < m < 2.
B. 1 ≤ m ≤ 2.
C. m ≥ 2 hoặc m ≤ 1.
D. m > 2 hoặc m < 1.
Lời giải:
Chọn A
Bài 7: Tìm m để hàm số 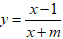
Lời giải:
Chọn D
Bài 8: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 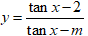
Lời giải:
Chọn A
Do tanx là hàm đồng biến trên khoảng 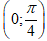
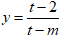
Bài 9: Tìm tất cả các giá trị của tham số thực m để hàm số 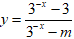
Lời giải:
Chọn C
Do đó hàm số 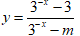
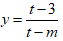
Bài 10: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = (m - 3)x - (2m + 1)cosx luôn nghịch biến trên R?
Lời giải:
Chọn A
Tập xác định: D = R.
Ta có: y' = m - 3 + (2m + 1)sinx
Hàm số nghịch biến trên R ⇔ y' ≤ 0, ∀ x ∈ R ⇔ (2m + 1)sinx ≤ 3-m, ∀ x ∈ R
Trường hợp 1: 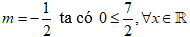
Trường hợp 2:
Trường hợp 3:
Bài 11: Hàm số y = x3 + 3x2 + mx + m đồng biến trên tập xác định khi giá trị của m là:
A. m ≤ 1
B. m ≥ 3
C. -1 ≤ m ≤ 3
D. m < 3
Lời giải
Chọn B
Tập xác định D = R
Tính đạo hàm y' = 3x2 + 6x + m
Để hàm số đồng biến trên R ⇔ y' ≥ 0 ⇔ 3x2 + 6x + m ≥ 0 với mọi x ∈ R (*)
⇔ Δ' ≤ 0 ⇔ 9 - 3m ≤ 0 ⇔ m ≥ 3
Bài 12: Tập hợp các giá trị m để hàm số y = mx3 - x2 + 3x + m - 2 đồng biến trên (-3;0) là
Lời giải
Chọn A
TXĐ: D = R
Ta có y' = 3mx2 - 2x + 3. Hàm số đồng biến trên khoảng (-3;0) khi và chỉ khi:
y' ≥ 0, ∀ x ∈ (-3;0) (Dấu "=" xảy ra tại hữu hạn điểm trên (-3;0))
Bài 13: Tìm tất cả giá trị của m để hàm số 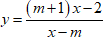
Lời giải
Chọn C
Hàm số đồng biến trên từng khoảng xác định khi và chỉ khi
y' > 0; ∀ x ∈ D ⇔ -m2 - m + 2 > 0 ⇔ -2 < m < 1
2. Bài tập tự luyện
Bài 1. Cho hàm số y = . Tìm các giá trị của m để hàm số đồng biến trên mỗi khoảng xác định của nó.
Bài 2. Tìm m để hàm số y = x3 + 3x2 + (m – 1)x + 4m nghịch biến trên khoảng (-1; 1).
Bài 3. Tìm m để hàm số y = x3 + (1 – 2m)x2 + (2 – m)x + m + 2 đồng biến trên khoảng (0;+∞).
Bài 4. Tìm m để hàm số y = nghịch biến trên khoảng (-∞; -1).
Bài 5. Tìm m để hàm số y = nghịch biến trên nửa khoảng [1; +∞].
Bài 6: Tìm tất cả các giá trị thực của tham số m sao cho hàm số: nghịch biến trên khoảng
Bài 7: Tìm tất cả các giá trị thực của tham số m sao cho hàm số nghịch biến trên khoảng
Bài 8: Với giá trị nào của m thì hàm số nghịch biến trên
Bài 9: Tìm m để hàm số đồng biến trên
Bài 10: Tìm m để hàm số đồng biến trên
Bài 11: Tìm m để hàm số nghịch biến trên
Bài 12: Tìm tất cả các giá trị của m để hàm số nghịch biến trên khoảng
Bài 13: Cho hàm số . Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng (17;37).
| A. m ∈ [-4; -1] | B. m ∈ (-∞; -6] ∪ [-4; -1) ∪ (2; +∞) |
| C. m ∈ (-∞; -4] ∪ (2; +∞) | D. m ∈ (-1; 2) |
Bài 14: Hàm số: y = 2x3 - 3(2m + 1)x2 + 6m(m + 1)x + 1 đồng biến trên khoảng (2;+∞) khi giá trị m là?
| A. m ≤ 2 | B. m ≥ 2 |
| C. m ≤ 1 | D. m ≥ 1 |
Bài 15: Cho hàm số: đồng biến trên từng khoảng xác định của nó khi giá trị của tham số m là:
| A. m < 0 | B. m > 0 |
| C. m = 0 | D. m ∈ R |
Bài 16: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2017 ] để hàm số y = (m - 2)x + 2m đồng biến trên R.
| A. 2014 | B. 2016 |
| C. vô số | D. 2015 |
Bài 17: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2017 ] để hàm số y =(m2-4)x + 2m đồng biến trên R.
| A. 4030 | B. 4034 |
| C. Vô số | D. 2015 |
Bài 18: Tìm tất cả các giá trị thực của tham số số m để hàm số đồng biến trên khoảng
| A. m ∈ (-∞ ; 0) ∪ (1 ;+∞) | B. m ∈ (-∞ ; 0) |
| C. m ∈ (1 ; +∞) | D. m ∈ (-∞ ; 1) |
Bài 19: Tìm tất cả các giá trị của tham số m để hàm số y = ln (16x2 + 1) - (m +1)x + m + 2 nghịch biến trên khoảng ( -∞; +∞)
| A. m ∈ (-∞ ; -3] | B. m ∈ [3 ; +∞ ) |
| C. m ∈ (-∞ ; -3) | D. m ∈ [-3 ; 3] |
Bài 20: Cho hàm số y = x3 + 3x2. Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số đồng biến trên (-∞ ; -2) và (0 ;+∞)
B. Hàm số nghịch biến trên (-2 ; 1)
C. Hàm số đồng biến trên khoảng (-∞ ; 0) và (2 ;+∞)
D. Hàm số nghịch biến trên khoảng (-∞ ; -2) và (0 ;+∞)