Với tóm tắt lý thuyết Toán lớp 9 Bài 3: Tiếp tuyến của đường tròn sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 3: Tiếp tuyến của đường tròn

A. Lý thuyết Tiếp tuyến của đường tròn

1. Nhận biết tiếp tuyến của đường tròn

Nhận xét: Nếu một đường thẳng là tiếp tuyến của một đường tròn thì đường thẳng đó vuông góc với bán kính đi qua tiếp điểm.

Dấu hiệu nhận biết tiếp tuyến

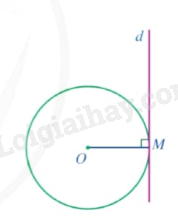
2. Tính chất của hai tiếp tuyến cắt nhau

Định lí

Ví dụ: Cho đường tròn (O), B, C $\in$ (O). Tiếp tuyến của (O) tại B và C cắt nhau tại A.

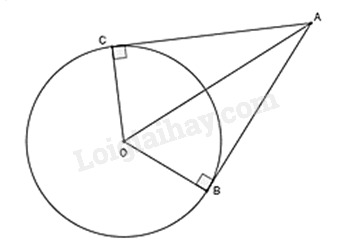
Khi đó:

- AB = AC

- Tia AO là tia phân giác của $\widehat{BAC}$.

- Tia OA là tia phân giác của $\widehat{BOC}$.

Sơ đồ tư duy Tiếp tuyến của đường tròn

B. Bài tập Tiếp tuyến của đường tròn

Bài 1. “Nếu một đường thẳng đi qua một điểm của đường tròn và ... thì đường thẳng đó là một tiếp tuyến của đường tròn.” Cụm từ thích hợp điền vào chỗ trống là

A. song song với bán kính đi qua điểm đó;

B. vuông góc với bán kính đi qua điểm đó;

C. song song với bán kính đường tròn;

D. vuông góc với bán kính bất kì.

Hướng dẫn giải

Đáp án đúng là: B

Dấu hiệu nhận biết tiếp tuyến của đường tròn: Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng đó là một tiếp tuyến của đường tròn.

Vậy ta chọn phương án B.

Bài 2. Cho hình vẽ

Giá trị của x trong hình vẽ trên là

A. $x=-\frac{2}{5};$

B. x = –1;

C. x = 3;

D. $x=\frac{2}{5};$

Hướng dẫn giải

Đáp án đúng là: C

Ta có AB, AC là hai tiếp tuyến của đường tròn (O), với B, C là tiếp điểm.

Áp dụng tính chất hai tiếp tuyến cắt nhau, ta được AB = AC.

Suy ra 7x – 4 = 3x + 8

Nên 4x = 12

Do đó x = 3.

Vậy x = 3 thỏa yêu cầu bài toán.

Bài 3. Cho đường tròn (O), điểm M nằm ngoài (O) sao cho MA, MB là hai tiếp tuyến (A, B là hai tiếp điểm). Biết $\widehat{MAB}=70°,$ số đo $\widehat{AOM}$ bằng

A. 70°;

B. 140°;

C. 35°;

D. 110°.

Hướng dẫn giải

Đáp án đúng là: A

Ta có AM là tiếp tuyến của (O) tại A nên AM ⊥ OA.

Do đó $\widehat{OAB}+\widehat{BAM}=90°.$

Vì vậy $\widehat{OAB}=90°-\widehat{BAM}=90°-70°=20°.$

Ta có tam giác OAB cân tại O (do OA = OB = R) nên $\widehat{OBA}=\widehat{OAB}=20°.$

Tam giác OAB, có: $\widehat{AOB}+\widehat{OBA}+\widehat{OAB}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{AOB}=180°-\left(\widehat{OBA}+\widehat{OAB}\right)=180°-\left(20°+20°\right)=140°.$

Ta có MA, MB là hai tiếp tuyến của đường tròn (O) nên OM là tia phân giác của $\widehat{AOB}$ (tính chất hai tiếp tuyến cắt nhau).

Do đó $\widehat{AOM}=\frac{\widehat{AOB}}{2}=\frac{140°}{2}=70°.$

Vậy ta chọn phương án A.

Bài 4. Cho tam giác ABC vuông tại A. Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại D (khác A). Chứng minh rằng CD là tiếp tuyến của đường tròn (B; BA).

Hướng dẫn giải

Xét đường tròn (B), có: BD = BA.

Xét đường tròn (C), có: CD = CA.

Xét ∆ABC và ∆DBC, có:

BA = BD;

CA = CD;

Cạnh BC là cạnh chung.

Do đó ∆ABC = ∆DBC (c.c.c).

Suy ra $\widehat{BDC}=\widehat{BAC}=90°$ hay CD ⊥ BD tại D, mà D thuộc (B; BA)

Vậy CD là tiếp tuyến của đường tròn (B; BA).

Bài 5. Cho đường tròn (O; R). Từ điểm A nằm ngoài đường tròn vẽ hai tiếp tuyến AB, AC với đường tròn (O), với B, C là tiếp điểm.

a) Chứng minh AO là đường trung trực của đoạn BC.

b) Kẻ đường kính CD của (O). Chứng minh BD // AO.

c) Kẻ OM vuông góc với OB (M thuộc AC). Chứng minh MO = MA.

Hướng dẫn giải

Vì AB, AC là tiếp tuyến của (O) nên AB = AC (tính chất hai tiếp tuyến cắt nhau)

Suy ra A thuộc đường trung trực của đoạn BC (1)

Lại có OA = OB = R.

Suy ra O thuộc đường trung trực của đoạn BC (2)

Từ (1), (2), ta thu được OA là đường trung trực của đoạn BC.

b) Tam giác BCD có OB = OC = OD = R và O là trung điểm CD (do CD là đường kính của (O)).

Do đó tam giác BCD vuông tại B hay BD ⊥ BC.

Mà AO ⊥ BC (do OA là đường trung trực của đoạn BC)

Vậy AO // BD.

c) Ta có OM ⊥ OB nên $\widehat{MOA}+\widehat{AOB}=90°$ (3)

Ta có AB, AC là hai tiếp tuyến của (O) nên AO là tia phân giác của $\widehat{BAC}$.

Do đó $\widehat{MAO}=\widehat{OAB}$ (4)

Ta có tam giác OAB vuông tại B (do AB là tiếp tuyến của (O)).

Suy ra $\widehat{AOB}+\widehat{OAB}=90°$ (5)

Từ (3), (4), (5), ta thu được $\widehat{MAO}=\widehat{MOA}.$

Do đó tam giác AMO cân tại M.

Vậy MA = MO.

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn

Lý thuyết Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn

Lý thuyết Bài 2: Vị trí tương đối của đường thẳng và đường tròn

Lý thuyết Bài 3: Tiếp tuyến của đường tròn

Lý thuyết Bài 4: Góc ở tâm. Góc nội tiếp

Lý thuyết Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên