Với tóm tắt lý thuyết Toán lớp 9 Bài 4: Góc ở tâm. Góc nội tiếp sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp

A. Lý thuyết Góc ở tâm. Góc nội tiếp

1. Góc ở tâm

Định nghĩa

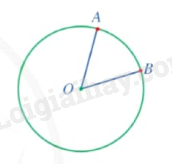
Nhận xét: Đường kính chia đường tròn thành hai phần, mỗi phần được gọi là một nửa đường tròn.

2. Cung, số đo cung

Cung

Phần đường tròn nối liền hai điểm A, B trên đường tròn được gọi là một cung (hay cung tròn) AB, kí hiệu là $\stackrel{⌢}{AB}$.

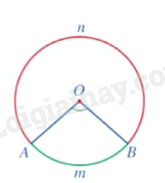
Góc ở tâm $\widehat{AOB}$ chắn cung AnB hay cung AnB bị chắn bởi góc ở tâm $\widehat{AOB}$.

$\stackrel{⌢}{AnB}$ là cung nhỏ và $\stackrel{⌢}{AmB}$ là cung lớn.

Số đo cung

Quy ước: Khi hai mút của cung trùng nhau, ta có “cung không” với số đo $0^0$ và cung cả đường tròn có số đo ${360}^0$.

Nhận xét: Góc ở tâm chắn một cung mà cung đó là nửa đường tròn thì có số đo bằng ${180}^0$.

Nếu điểm C là một điểm nằm trên cung AB thì sđ$\stackrel{⌢}{ACB}$ = sđ$\stackrel{⌢}{AC}$ + sđ$\stackrel{⌢}{CB}$.

Chú ý:

- Khác với so sánh hai góc, ta chỉ so sánh hai cung trong một đường tròn hay trong hai đường tròn bằng nhau. Cụ thể:

+ Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau;

+ Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

Hai cung AB và CD bằng nhau được kí hiệu là $\stackrel{⌢}{AB}=\stackrel{⌢}{CD}$.

Cung EG nhỏ hơn cung HK được kí hiệu là $\stackrel{⌢}{EG}<\stackrel{⌢}{HK}$. Trong trường hợp này, ta cũng nói cung HK lớn hơn cung EG và kí hiệu là $\stackrel{⌢}{HK}>\stackrel{⌢}{EG}$.

- Cho điểm $A$ thuộc đường tròn $(O)$ và số thực $\alpha$ với $0<\alpha <360$. Sử dụng thược thẳng và thước đo độ, ta vẽ điểm $B$ thuộc đường tròn $(O)$ như sau:

+ Nếu $0<\alpha \le 180$ thì ta vẽ theo chiểu quay của kim đồng hồ góc ở tâm AOB có số đo bằng ${\alpha }^0$. Khi đó sđ$\stackrel{⌢}{AmB}={\alpha }^0$

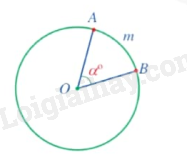
+ Nếu $180<\alpha \le 360$ thì ta vẽ theo ngược chiểu quay của kim đồng hồ góc ở tâm AOB có số đo bằng ${\alpha }^0-{180}^0$. Khi đó sđ$\stackrel{⌢}{AnB}={\alpha }^0$.

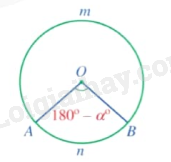
3. Góc nội tiếp

Định nghĩa

Định lí

Số đo góc nội tiếp

Ví dụ:

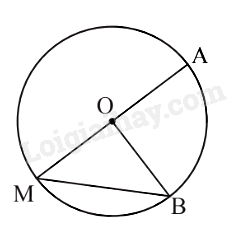
$\widehat{AMB}$ là góc nội tiếp chắn $\stackrel{⌢}{AB}$ trên đường tròn (O) nên $\widehat{AMB}=\frac{1}{2}$sđ$\stackrel{⌢}{AB}$.

Nhận xét: Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.

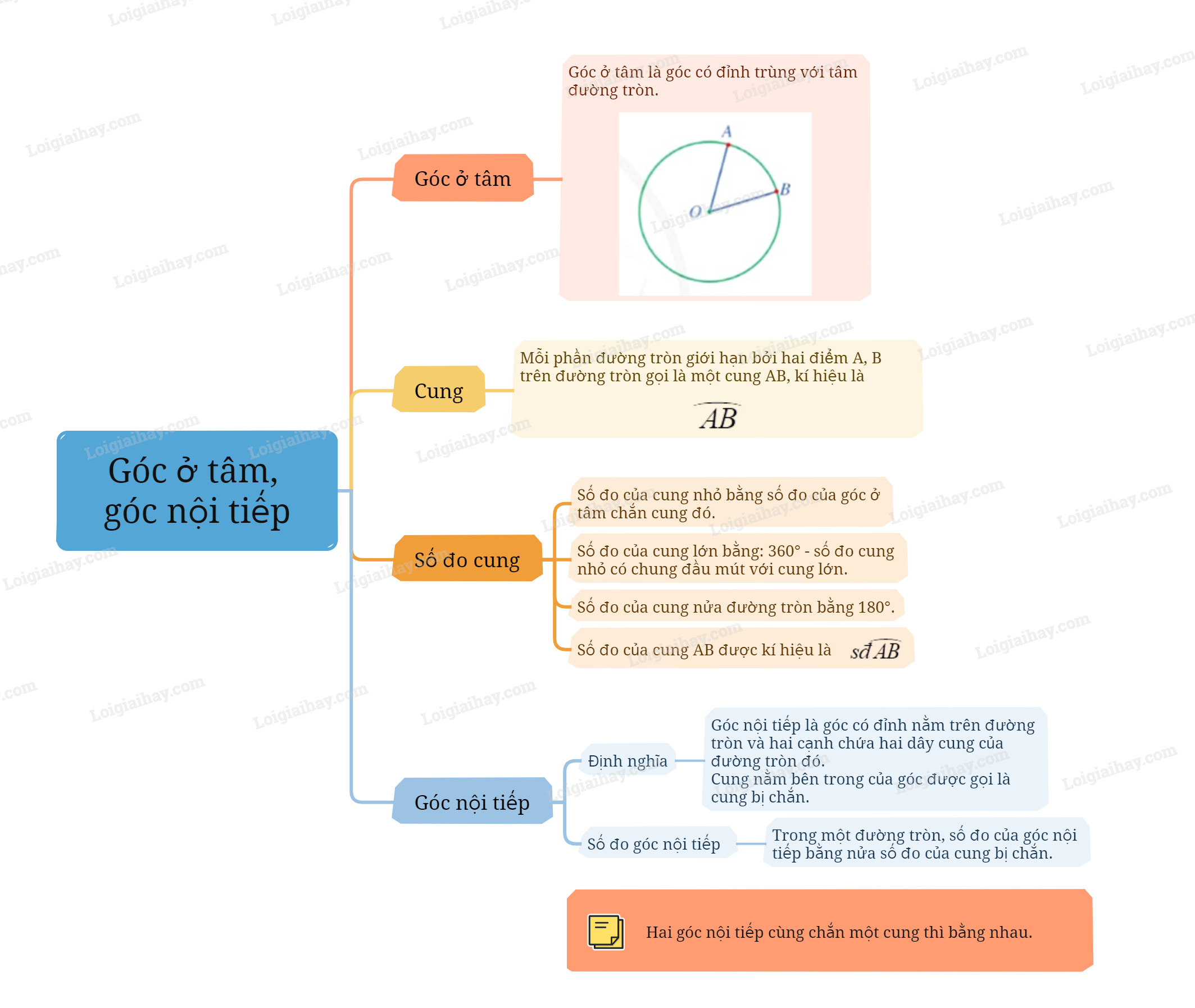
Sơ đồ tư duy Góc ở tâm. Góc nội tiếp

B. Bài tập Góc ở tâm. Góc nội tiếp

Bài 1. Góc ở tâm là góc

A. có đỉnh nằm trên đường tròn;

B. có hai cạnh là hai dây của đường tròn;

C. có đỉnh nằm trên bán kính của đường tròn;

D. có đỉnh trùng với tâm của đường tròn.

Hướng dẫn giải

Đáp án đúng là: D

Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn.

Vậy ta chọn phương án D.

Bài 2. Hình nào sau đây biểu diễn góc nội tiếp?

A. Hình 1;

B. Hình 2;

C. Hình 3;

D. Hình 4.

Hướng dẫn giải

Đáp án đúng là: B

Hình 1 biểu diễn góc ở tâm $\widehat{AOB}$ vì có đỉnh trùng với tâm của đường tròn.

Hình 2 biểu diễn góc nội tiếp $\widehat{DEF}$ vì có đỉnh nằm trên đường tròn và hai cạnh DE, DF chứa hai dây cung của đường tròn.

Hình 3, Hình 4 không phải là góc nội tiếp vì có đỉnh không nằm trên đường tròn.

Vậy ta chọn phương án B.

Bài 3. Góc nội tiếp chắn nửa đường tròn có số đo là

A. 60°;

B. 90°;

C. 120°;

D. 180°.

Hướng dẫn giải

Đáp án đúng là: B

Góc nội tiếp chắn nửa đường tròn có số đo là 90°.

Vậy ta chọn phương án B.

Bài 4. Cho tam giác ABC cân tại A có $\hat{A}<90°.$ Vẽ đường tròn đường kính AB cắt BC tại D, cắt AC tại E. Chứng minh rằng:

a) Tam giác DBE cân.

b) $\widehat{CBE}=\frac{1}{2}\widehat{BAC}.$

Hướng dẫn giải

Vì D, E nằm trên đường tròn đường kính AB nên $\widehat{ADB},\widehat{AEB}$ là hai góc nội tiếp chắn nửa đường tròn, do đó $\widehat{ADB}=\widehat{AEB}=90°.$

Suy ra AD ⊥ BC và BE ⊥ AC.

Tam giác ABC cân tại A có AD là đường cao nên AD cũng là đường trung tuyến của tam giác.

Do đó D là trung điểm BC nên $DB=DC=\frac{1}{2}BC.$

Tam giác BEC vuông tại C có ED là đường trung tuyếnứng với cạnh huyền BC nên $ED=\frac{1}{2}BC.$

Suy ra DE = DB = DC.

Vậy tam giác BDE cân tại D.

b) Tam giác ABC cân tại A có AD là đường cao nên AD cũng là đường phân giác của tam giác ABC, do đó $\widehat{CAD}=\widehat{BAD}=\frac{1}{2}\widehat{BAC}.$

Mà $\widehat{DBE}=\widehat{DAE}$ (hai góc nội tiếp cùng chắn cung DE của đường tròn đường kính AB)

Do đó $\widehat{DBE}=\widehat{BAD}=\frac{1}{2}\widehat{BAC}.$

Vậy$\widehat{CBE}=\frac{1}{2}\widehat{BAC}.$

Bài 5. Cho đường tròn (O) và hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung nhỏ AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng $\widehat{MSD}=2\widehat{MBA}.$

Hướng dẫn giải

Vì SM là tiếp tuyến của (O) tại M nên $\widehat{OMS}=90°.$

Tam giác OMS vuông tại M, có: $\widehat{O_1}+\widehat{OSM}=90°$ (hai góc nhọn trong tam giác vuông bằng 90°).

Mà $\widehat{O_1}+\widehat{O_2}=90°$ (do AB ⊥ CD) nên $\widehat{OSM}=\widehat{O_2}.$ (1)

Mặt khác, $\widehat{O_2}$ và $\widehat{MBA}$ lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung AM của đường tròn (O) nên $\widehat{MBA}=\frac{1}{2}\widehat{O_2}$ hay$\widehat{O_2}=2\widehat{MBA}.$ (2)

Từ (1), (2), ta có$\widehat{MSD}=2\widehat{MBA}.$

Bài 6. Xác định số đo cung nhỏ AB trong hình ngôi sao năm cánh sau biết các đỉnh của ngôi sao chia đường tròn thành các cung bằng nhau:

Hướng dẫn giải

Vì số đo của cung cả đường tròn gấp năm lần số đo cung nhỏ AB và cung cả đường tròn có số đo bằng 360° nên sđ$\stackrel{⏜}{AB}=\frac{1}{5}\cdot 360°=72°.$

Vậy số đo cung nhỏ AB trong hình ngôi sao năm cánh đã cho bằng 72°.

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn

Lý thuyết Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn

Lý thuyết Bài 2: Vị trí tương đối của đường thẳng và đường tròn

Lý thuyết Bài 3: Tiếp tuyến của đường tròn

Lý thuyết Bài 4: Góc ở tâm. Góc nội tiếp

Lý thuyết Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên