Với giải sách bài tập Toán 9 Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:

Giải SBT Toán 9 Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 10 trang 84 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại C có $AC=\frac{5}{13}AB.$ Tính sin A và tan B.

Lời giải:

Vì tam giác ABC vuông tại C, theo định lí Pythagore ta có:

AB² = AC² + BC²

Suy ra BC² = AB² – AC²

       $=A{B}^2={\left(\frac{5}{13}AB\right)}^2=A{B}^2-\frac{25}{169}A{B}^2=\frac{144}{169}A{B}^2.$

Do đó $BC=\sqrt{\frac{144}{169}A{B}^2}=\sqrt{{\left(\frac{12}{13}AB\right)}^2}=\frac{12}{13}AB.$

Vậy $\sin A=\frac{BC}{AB}=\frac{\frac{12}{13}AB}{\frac{12}{13}AB}=\frac{12}{13};\tan B=\frac{AC}{BC}=\frac{\frac{5}{13}AB}{\frac{12}{13}AB}=\frac{5}{12}.$

Bài 11 trang 84 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A có AB = 21 cm, $\widehat{C}=47°.$ Tính độ dài đường phân giác BD của tam giác ABC (làm tròn kết quả đến hàng phần trăm của centimet).

Lời giải:

Trong tam giác vuông ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{B}=180°-\widehat{A}-\widehat{C}=180°-90°-47°=43°.$

Mà BD là phân giác góc B nên $\widehat{B_1}=\widehat{B_2}=\frac{1}{2}\widehat{B}=\frac{1}{2}\cdot 43°=21,5°.$

Vì tam giác ABD vuông tại A nên $\cos \widehat{B_1}=\frac{AB}{BD}.$

Suy ra $BD=\frac{AB}{\cos \widehat{B_1}}=\frac{21}{\cos 21,5°}\approx 22,57 ( \text{cm}).$

Bài 12 trang 85 SBT Toán 9 Tập 1: Cho tam giác ABC có AB = 6 cm, $\widehat{A}=15°,\widehat{B}=35°.$ Tính độ dài đường cao CH của tam giác ABC (làm tròn kết quả đến hàng phần trăm của centimét).

Lời giải:

Do CH là đường cao tam giác ABC nên CH ⊥ AB tại H.

Tam giác ACH vuông tại H nên $AH=CH\cdot \cot \widehat{A}=CH\cdot \cot 15°.$

Tam giác BCH vuông tại H nên $BH=CH\cdot \cot \widehat{B}=CH\cdot \cot 35°.$

Mà AH + BH = AB

Suy ra CH.cot15° + CH.cot35° = AB hay CH(cot15° + cot35°) = AB

Suy ra $CH=\frac{AB}{\cot 15°+\cot 35°}=\frac{6}{\cot 15°+\cot 35°}\approx 1,16\left(cm\right).$

Bài 13 trang 85 SBT Toán 9 Tập 1: Tìm x, y trong mỗi hình 14a, 14b, 14c (làm tròn kết quả đến hàng phần mười của centimét).

Lời giải:

⦁ Hình 14a):

Trong tam giác ABD vuông tại D có:

$\sin \widehat{B}=\frac{AD}{AB}$ hay $\sin 32°=\frac{x}{9}$

Suy ra x = 9.sin 32° ≈ 4,8 cm.

Trong tam giác ADC vuông tại D có:

$\cos \widehat{CAD}=\frac{AD}{AC}$ hay $\cos 50°\approx \frac{4,8}{y}$

Suy ra $y\approx \frac{4,8}{\cos 50°}\approx 7,5cm.$

⦁ Hình 14b):

Trong tam giác GHK vuông tại K có $\widehat{H}=45°$ nên tam giác GHK vuông cân tại K.

Suy ra GK = HK = 5 cm.

Áp dụng định lí Pythagore cho tam giác GHK vuông tại K, ta có:

HG² = HK² + GK² = 5² + 5² = 50.

Suy ra $HG=\sqrt{50}\approx 7,1cm$ hay x ≈ 7,1 cm.

Trong tam giác GIK vuông tại K có:

$\sin \widehat{I}=\frac{GK}{GI}$ hay $\sin 36°=\frac{5}{y}$

Suy ra $y=\frac{5}{\sin 36°}\approx 8,5cm.$

⦁ Hình 14c):

Trong tam giác MOQ vuông cân tại Q có:

MO² = QM² + QO² hay ${\left(2\sqrt{2}\right)}^2=2Q{M}^2$

Do đó 2QM² = 8 nên QM² = 4

Suy ra OP = QO = QM = 2 cm.

Mặt khác, $\widehat{MOQ}+\widehat{MON}+\widehat{NOP}=180°$

Mà $\widehat{MOQ}=45°$ (do tam giác MOQ vuông cân tại Q) và $\widehat{MON}=105°$

Suy ra $\widehat{NOP}=180°-\widehat{MOQ}-\widehat{MON}=180°-45°-105°=30°.$

Trong tam giác ONP vuông tại P có:

⦁ $x=NP=OP\cdot \tan \widehat{NOP}=2\cdot \tan 30°=2\cdot \frac{\sqrt{3}}{3}\approx 1,2cm;$

⦁ $\cos \widehat{NOP}=\frac{OP}{ON}$ suy ra $y=ON=\frac{OP}{\cos \widehat{NOP}}=\frac{2}{\cos 30°}=\frac{2}{\frac{\sqrt{3}}{2}}=\frac{4}{\sqrt{3}}=\frac{4\sqrt{3}}{3}\approx 2,3cm.$

Bài 14 trang 85 SBT Toán 9 Tập 1: Chứng minh diện tích của tam giác đều cạnh a là $\frac{a^2\sqrt{3}}{4}.$.

Lời giải:

Xét tam giác đều ABC cạnh a với đường cao AH.

Khi đó, ta có AB = BC = a và $\widehat{B}=60°.$

Vì tam giác ABH vuông tại H nên

$AH=AB\cdot \sin \widehat{B}=a\cdot \sin 60°=\frac{a\sqrt{3}}{2}.$

Vậy diện tích của tam giác ABC là:

$\frac{1}{2}BC\cdot AH=\frac{1}{2}\cdot a\cdot \frac{a\sqrt{3}}{2}=\frac{a^2\sqrt{3}}{4}.$

Bài 15 trang 85 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A. Chứng minh:

$\tan \frac{\widehat{B}}{2}=\frac{AC}{AB+BC}.$

Lời giải:

Kẻ đường phân giác BD của tam giác ABC. Khi đó, ta có $\widehat{B_1}=\frac{\widehat{B}}{2}.$

Vì tam giác ABD vuông tại A nên $\tan \widehat{B_1}=\frac{AD}{AB}.$

Theo tính chất đường phân giác, ta có: $\frac{AD}{CD}=\frac{AB}{BC}$ hay $\frac{AD}{AB}=\frac{CD}{BC}.$

Theo tính chất dãy tỉ số bằng nhau, ta có:

$\frac{AD}{AB}=\frac{CD}{BC}=\frac{AD+CD}{AB+BC}=\frac{AC}{AB+BC}.$

Vậy $\tan \widehat{B_1}=\frac{AC}{AB+BC}$ hay $\tan \frac{\widehat{B}}{2}=\frac{AC}{AB+BC}.$

Bài 16 trang 85 SBT Toán 9 Tập 1: Hai khinh khí cầu được thả lên cùng độ cao là 350 m (ở hai vị trí A và B). Tại vị trí C trên mặt đất, người ta quan sát và đo được $\widehat{ACH}=40°,\widehat{ACB}=10°$ (Hình 15). Tính khoảng cách giữa hai khinh khí cầu (làm tròn kết quả đến hàng đơn vị của mét).

Lời giải:

Vì tam giác ACH vuông tại H nên $CH=AH\cdot \cot \widehat{ACH}=350\cdot \cot 40°.$

Ta có: $\widehat{BCK}=\widehat{BCA}+\widehat{ACH}=10°+40°=50°.$

Vì tam giác BCK vuông tại K nên $CK=BK\cdot \cot \widehat{BCK}=350\cdot \cot 50°.$

Do BK ⊥ CH tại K, AH ⊥ CH tại H suy ra BK // AH.

Mà BK = AH = 350 m

Nên ABKH là hình bình hành.

Suy ra khoảng cách giữa hai khinh khí cầu là:

AB = HK = CH ‒ CK

= 350.cot 40° ‒ 350.cot 50°

= 350.(cot 40° ‒ cot 50°)

≈ 123 m.

Vậy khoảng cách giữa hai khinh khí cầu là khoảng 123 mét.

Bài 17 trang 85 SBT Toán 9 Tập 1: Bạn Đức đứng trên nóc ngôi nhà ở độ cao 8 m. Vị trí mắt bạn Đức (tại vị trí A) cách nóc nhà 1,5 m. Bạn nhìn thấy vị trí B cao nhất của một toà nhà với góc tạo bởi tia AB và tia AH theo phương nằm ngang là $\widehat{BAH}=60°.$ Bạn Đức cũng nhìn thấy vi trí K tại chân toà nhà đó với góc tạo bới tia AK và tia AH là $\widehat{HAK}=15°,$ AH vuông góc với BK tại H (Hình 10). Tính chiều cao BK của toà nhà (làm tròn kết quả đến hàng phần mười của mét).

Lời giải:

Do AH ⊥ BK tại H, AC ⊥ CK, CK ⊥ BK nên $\widehat{ACK}=\widehat{AHK}=\widehat{CKH}=90°$

Do đó tứ giác ACHK là hình chữ nhật.

Suy ra HK = AC = 1,5 + 8 = 9,5 m.

Vì ∆AHK vuông tại H nên $AH=HK\cdot \cot \widehat{HAK}=9,5\cdot \cot 15°.$

Vì ∆AHB vuông tại H nên $BH=AH\cdot \tan \widehat{BAH}=9,5\cdot \cot 15°\cdot \tan 60°.$

Chiều cao của toà nhà là:

BK = HK + BH

= 9,5 + 9,5.cot 15°.tan 60°

= 9,5.(1 + cot 15°.tan 60°)

≈ 70,9 (m).

Vậy chiều cao của tòa nhà khoảng 70,9 mét.

Xem thêm các bài giải Sách bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

Bài 1: Tỉ số lượng giác của góc nhọn

Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn

Bài tập cuối chương 4

Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn

Bài 2: Vị trí tương đối của đường thẳng và đường tròn

Lý thuyết Một số hệ thức về cạnh và góc trong tam giác vuông

1. Tính cạnh góc vuông theo cạnh huyền và tỉ số lượng giác của góc nhọn

Ví dụ 1:

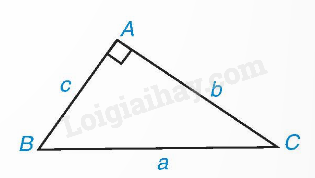
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=a.\sin B=a.\cos C;\\ c=a.\sin C=a.\cos B.\end{array}$

2. Tính cạnh góc vuông theo cạnh góc vuông còn lại và tỉ số lượng giác của góc nhọn

Ví dụ 2:

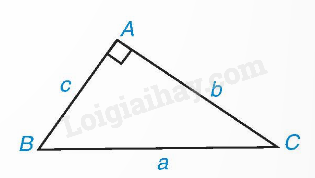
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=c.\tan B=c.\cot C;\\ c=b.\tan C=b.\cot B.\end{array}$

3. Áp dụng tỉ số lượng giác của góc nhọn để giải tam giác vuông

Giải tam giác vuông là tìm tất cả độ dài các cạnh và số đo các góc còn lại của tam giác đó.