Với giải Bài 5 trang 28 Chuyên đề Toán 12 Cánh diều chi tiết trong Bài 1: Vận dụng hệ bất phương trình bậc nhất để giải quyết một số bài toán quy hoạch tuyến tính giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề Toán 12. Mời các bạn đón xem:

Giải Chuyên đề Toán 12 Bài 1: Vận dụng hệ bất phương trình bậc nhất để giải quyết một số bài toán quy hoạch tuyến tính

Bài 5 trang 28 Chuyên đề Toán 12: Bác Dũng đầu tư không quá 1,2 tỉ đồng vào hai loại cổ phiếu: cổ phiếu A dự kiến chi trả cổ tức bằng tiền với tỉ lệ 5%; cổ phiếu B rủi ro cao dự kiến chi trả cổ tức bằng tiền với tỉ lệ 12%. Giá cổ phiếu A là 30 000 đồng/1 cổ phiếu, giá cổ phiếu B là 40 000 đồng/1 cổ phiếu. Để giảm thiểu rủi ro, bác Dũng quyết định mua số lượng cổ phiếu B không quá 10 000 cổ phiếu. Hỏi bác Dũng nên đầu tư mỗi loại bao nhiêu cổ phiếu để lợi nhuận thu được là lớn nhất?

Lời giải:

Gọi bác Dũng cần mua x cổ phiếu A và y cổ phiếu B (x ∈ ℕ, y ∈ ℕ).

Khi đó, số tiền bác Dũng cần chi ra là: 30 000x + 40 000y (đồng).

Vì số tiền bác Dũng đầu tư không quá 1,2 tỉ đồng nên ta có:

30 000x + 40 000y ≤ 1 200 000 000 hay 3x + 4y ≤ 120 000.

Vì số lượng cổ phiếu B được mua không quá 10 000 cổ phiếu nên y ≤ 10 000.

Một cổ phiếu A sẽ nhận được số tiền chi trả cổ tức là: 5% . 30 000 = 1 500 (đồng).

Một cổ phiếu B sẽ nhận được số tiền chi trả cổ tức là: 12% . 40 000 = 4 800 (đồng).

Do đó, bác Dũng nhận được số tiền chi trả cổ tức là: T = 1 500x + 4 800y (đồng).

Vì vậy, yêu cầu của bác Dũng có thể viết ở dạng tổng quát của bài toán quy hoạch tuyến tính sau:

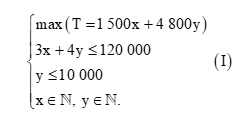
Xét hệ bất phương trình bậc nhất hai ẩn (x, y là các số thực): $\left\{\begin{array}{l}3x+4y\le 120000\\ y\le 10000\\ x\ge 0\\ y\ge 0.\end{array}\right.\left(I^{\text{'}}\right)$

Ta cần tìm giá trị lớn nhất của biểu thức T = 1 500x + 4 800y khi (x; y) thỏa mãn hệ bất phương trình (I’).

Bước 1. Xác định miền nghiệm của hệ bất phương trình (I’).

Miền nghiệm là miền tứ giác OABC với tọa độ các đỉnh O(0; 0), A(0; 10 000), $B\left(\frac{80000}{3};10000\right),$ C(40 000; 0) (hình vẽ).

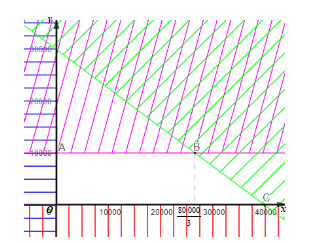
Bước 2. Tính giá trị của biểu thức T(x; y) = 1 500x + 4 800y tại các đỉnh của tứ giác này:

T(0; 0) = 0; T(0; 10 000) = 48 000 000;

$T\left(\frac{80000}{3};10000\right)=88000000;$ T(40 000; 0) = 60 000 000.

Bước 3. Ta đã biết biểu thức T = 1 500x + 4 800y đạt giá trị lớn nhất tại cặp số thực (x; y) là tọa độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của T ở Bước 2, kết hợp điều kiện x và y là các số tự nhiên, ta được giá trị lớn nhất cần tìm là T(40 000; 0) = 60 000 000.

Vậy bác Dũng nên đầu tư loại A 40 000 cổ phiếu để lợi nhuận thu được là lớn nhất.