Cho tam giác đều ABC có độ dài cạnh a. Tính độ dài đường cao AH của tam giác ABC theo a

Cho tam giác đều ABC có độ dài cạnh a. Tính độ dài đường cao AH của tam giác ABC theo a

Trịnh Thị Thu Hiền Ngày: 29-07-2024 Lớp 9

216

Với giải Bài 7 trang 60 Toán 9 Tập 1 Cánh diều chi tiết trong Bài 2: Một số phép tính về căn bậc hai của số thực giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực

Bài 7 trang 60 Toán 9 Tập 1: Cho tam giác đều ABC có độ dài cạnh a. Tính độ dài đường cao AH của tam giác ABC theo a.

Lời giải:

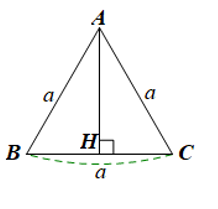
Cho một tam giác đều cạnh a. a) Tính độ dài đường cao của tam giác đó theo a. (ảnh 1)

Do AH là đường cao của tam giác đều ABC.

Suy ra AH đồng thời là đường trung tuyến của tam giác ABC.

Suy ra H là trung điểm của BC.

Suy ra $H B = H C = \frac{1}{2} B C = \frac{1}{2} a$ .

Xét tam giác AHB vuông tại H có:

$A H^{2} + H B^{2} = A B^{2}$ (Định lý Py – ta – go)

$\begin{array}{l} A H^{2} + {(\frac{a}{2})}^{2} = a^{2} \\ A H^{2} = a^{2} - {(\frac{a}{2})}^{2} = a^{2} - \frac{a^{2}}{4} = \frac{4 a^{2}}{4} - \frac{a^{2}}{4} = \frac{3 a^{2}}{4} \\ A H = \frac{a \sqrt{3}}{2} . \end{array}$

Vậy $A H = \frac{a \sqrt{3}}{2}$ .

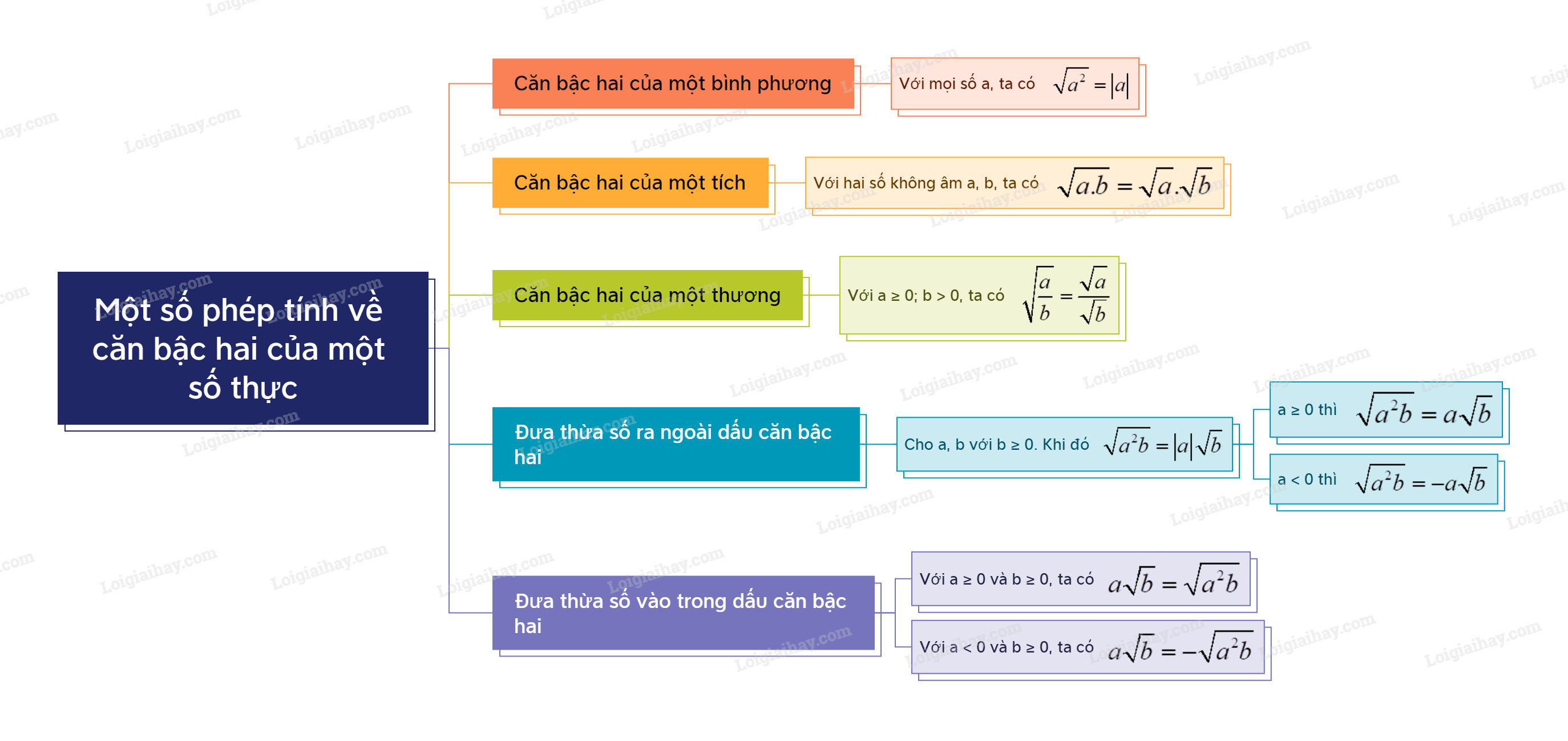
Sơ đồ tư duy Một số phép tính về căn bậc hai của số thực

Xem thêm lời giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

Khởi động trang 55 Toán 9 Tập 1: Khi một quả bóng rổ được thả xuống, nó sẽ nảy trở lại, nhưng do tiêu hao năng lượng nên nó không đạt dược chiều cao như lúc bắt đầu. Hệ số phục hồi của quả bóng rổ được tính theo công thức $C_{R} = \sqrt{\frac{h}{H}}$ , trong đó H là độ cao mà quả bóng được thả rơi và h là độ cao mà quả bóng bật lại......

Hoạt động 1 trang 55 Toán 9 Tập 1: So sánh......

Luyện tập 1 trang 55 Toán 9 Tập 1: Tính:.....

Hoạt động 2 trang 56 Toán 9 Tập 1: So sánh: $\sqrt{4.25}$ và $\sqrt{4} . \sqrt{25}$ ......

Luyện tập 2 trang 56 Toán 9 Tập 1: Áp dụng quy tắc về căn bậc hai của một tích, hãy tính:.....

Hoạt động 3 trang 57 Toán 9 Tập 1: So sánh $\sqrt{\frac{16}{25}}$ và $\frac{\sqrt{16}}{\sqrt{25}}$ ......

Luyện tập 3 trang 57 Toán 9 Tập 1: Trong tình huống nêu ra ở phần mở đầu, viết hệ số phục hồi của quả bóng rổ dưới dạng phân số.....

Hoạt động 4 trang 57 Toán 9 Tập 1: So sánh:.....

Luyện tập 4 trang 58 Toán 9 Tập 1: Rút gọn biểu thức: $\sqrt{3} + \sqrt{12} - \sqrt{27}$ ......

Hoạt động 5 trang 58 Toán 9 Tập 1: So sánh:.....

Luyện tập 5 trang 59 Toán 9 Tập 1: Rút gọn biểu thức:.....

Bài 1 trang 59 Toán 9 Tập 1: Tính:....

Bài 2 trang 59 Toán 9 Tập 1: Áp dụng quy tắc về căn bậc hai của một tích, hãy tính:......

Bài 3 trang 59 Toán 9 Tập 1: Áp dụng quy tắc về căn bậc hai của một thương, hãy tính:.....

Bài 4 trang 59 Toán 9 Tập 1: Áp dụng quy tắc đưa thừa số ra ngoài dấu căn bậc hai, hãy rút gọn biểu thức:....

Bài 5 trang 59 Toán 9 Tập 1: Áp dụng quy tắc đưa thừa số vào trong dấu căn bậc hai, hãy rút gọn biểu thức:.....

Bài 6 trang 60 Toán 9 Tập 1: So sánh:.....

Bài 7 trang 60 Toán 9 Tập 1: Cho tam giác đều ABC có độ dài cạnh a. Tính độ dài đường cao AH của tam giác ABC theo a.....

Bài 8 trang 60 Toán 9 Tập 1: Trong Vật lí, ta có định luật Joule – Lenz để tính nhiệt lượng tỏa ra ở dây dẫn khi có dòng điện chạy qua: $Q = I^{2} R t$ .....

Bài 9 trang 60 Toán 9 Tập 1: Tốc độ gần đúng của một ô tô ngay trước khi đạp phanh được tính theo công thức $v = \sqrt{2 λ g d}$ , trong đó $v (m / s)$ là tốc độ của ô tô, $d (m)$ là chiều dài của vết trượt tính từ thời điểm đạp phanh cho đến khi ô tô dừng lại trên đường, $λ$ là hệ số cản lăn của mặt đường, $g = 9, 8 m / s^{2}$ . Nếu một ô tô để lại vết trượt dài khoảng 20m trên đường nhựa thì tốc độ của ô tô trước khi đạp phanh là khoảng bao nhiêu mét trên giây (làm tròn đến kết quả đến hàng đơn vị)? Biết rằng hệ số cản lăn của đường nhựa là $λ = 0, 7$ .....

Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

§1. Căn bậc hai và căn bậc ba của số thực

§2. Một số phép tính về căn bậc hai của số thực

§3. Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

§4. Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Bài tập cuối chương 3

§1. Tỉ số lượng giác của góc nhọn

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

176

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

148

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

121

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

118

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.