Với giải Bài 6 trang 56 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Bài 6 trang 56 Toán 9 Tập 1: Chứng minh rằng:
a) với a > 0; b > 0
b) với a 0 và a 1
Lời giải:
a) với a > 0; b > 0
Xét vế trái ta có:
= VP
b) với a 0 và a 1
Xét vế trái ta có:
= VP.
Sơ đồ tư duy Biến đổi đơn giản biểu thức chứa căn thức bậc hai
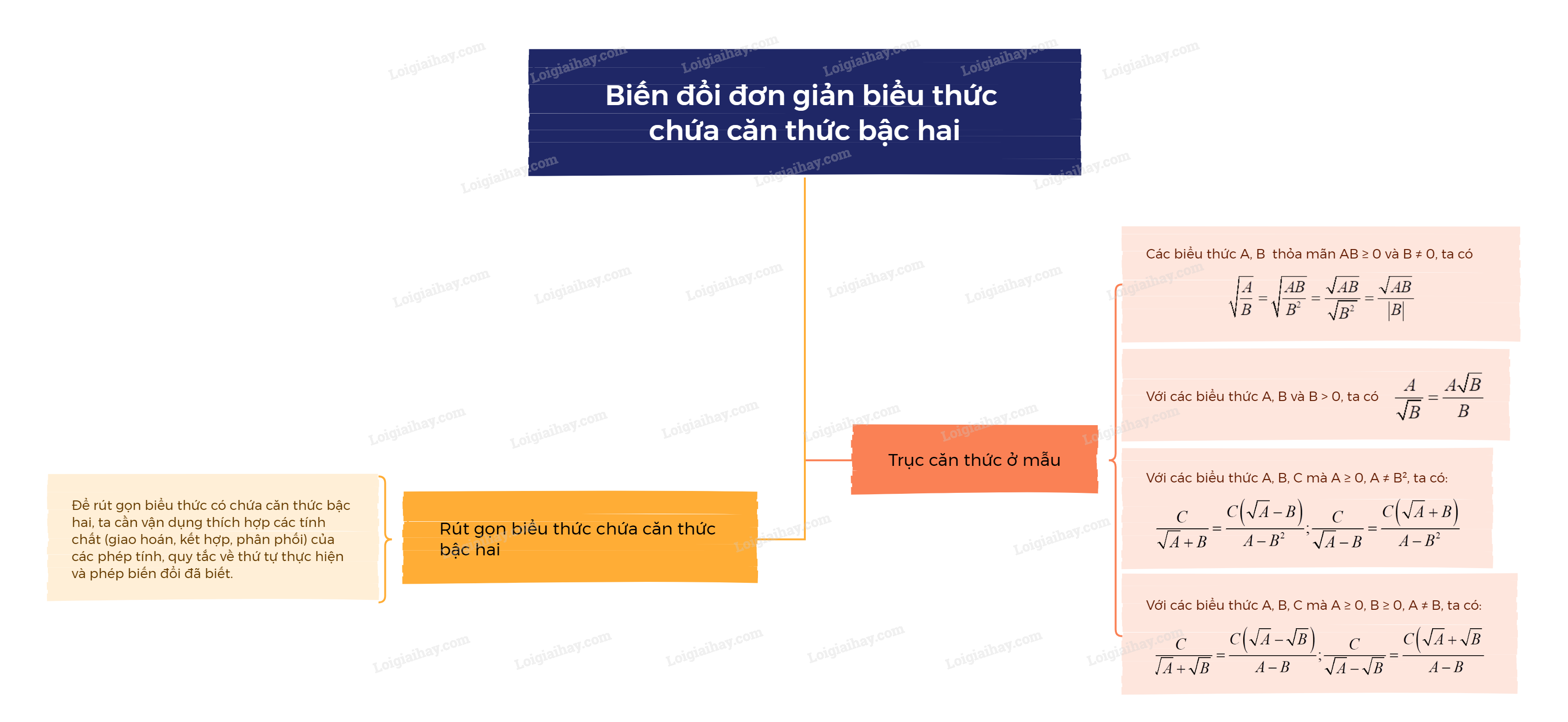
Xem thêm lời giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Vận dụng 2 trang 56 Toán 9 Tập 1: Trả lời câu hỏi trong hoạt động khởi động trang 52......
Bài 1 trang 56 Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau:......
Bài 2 trang 56 Toán 9 Tập 1: Khử mẫu của biểu thức lấy căn:.....
Bài 3 trang 56 Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau:......
Bài 4 trang 56 Toán 9 Tập 1: Rút gọn các biểu thức sau:......
Bài 5 trang 56 Toán 9 Tập 1: Tính......
Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 3. Tính chất của phép khai phương
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Bài 1. Tỉ số lượng giác của góc nhọn
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
