Giải SGK Toán 9 Bài 4 (Chân trời sáng tạo): Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Van Anh Ngày: 23-09-2024 Lớp 9

1 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai chi tiết sách Toán 9 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Hoạt động khám phá 1 trang 52 Toán 9 Tập 1: Bốn ô cửa hình vuông diện tích $\frac{1}{2} m^{2}$ ghép thành cửa sổ Hình 1.

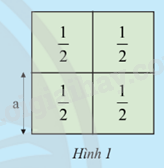
Giải SGK Toán 9 Bài 4 (Chân trời sáng tạo): Biến đổi đơn giản biểu thức chứa căn thức bậc hai (ảnh 1)

a) Hai bạn An và Mai tính độ dài cạnh a (m) của mỗi ô cửa.

Giải SGK Toán 9 Bài 4 (Chân trời sáng tạo): Biến đổi đơn giản biểu thức chứa căn thức bậc hai (ảnh 2)

Kết quả của mỗi bạn có đúng không? Giải thích?

b) Biết rằng $\sqrt{2} \approx 1, 4142$ . Không dùng máy tính cầm tay, hai bạn tìm giá trị gần đúng của độ dài mỗi ô cửa.

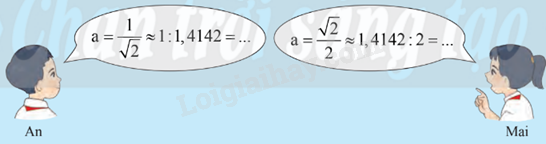
Giải SGK Toán 9 Bài 4 (Chân trời sáng tạo): Biến đổi đơn giản biểu thức chứa căn thức bậc hai (ảnh 3)

Theo em, bạn nào sẽ tìm ra đáp án nhanh hơn?

Lời giải:

a) Diện tích một hình vuông: S = $\frac{1}{2}$ (m²)

Mà S = a² suy ra a = $\sqrt{S} = \sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$ (m)

Vậy kết quả của 2 bạn đều đúng.

b) Theo em, bạn An sẽ tìm đáp án nhanh hơn.

Vì bạn An chỉ cần tính $\sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}}$ .

1. Trục căn thức ở mẫu

Thực hành 1 trang 54 Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau:

a) $\frac{\sqrt{7}}{\sqrt{3}}$

b) $- \frac{10}{3 \sqrt{5}}$

c) $\frac{2 \sqrt{2}}{\sqrt{40}}$

d) $\frac{\sqrt{2}}{\sqrt{5} - \sqrt{2}}$

Lời giải:

a) $\frac{\sqrt{7}}{\sqrt{3}} = \frac{\sqrt{7} . \sqrt{3}}{\sqrt{3} . \sqrt{3}} = \frac{\sqrt{21}}{3}$

b) $- \frac{10}{3 \sqrt{5}} = - \frac{10. \sqrt{5}}{3 \sqrt{5} . \sqrt{5}} = - \frac{10 \sqrt{5}}{15}$

c) $\frac{2 \sqrt{2}}{\sqrt{40}} = \frac{2 \sqrt{2} . \sqrt{40}}{\sqrt{40} . \sqrt{40}} = \frac{8 \sqrt{5}}{40} = \frac{\sqrt{5}}{5}$

d) $\frac{\sqrt{2}}{\sqrt{5} - \sqrt{2}}$ $= \frac{\sqrt{2} . (\sqrt{5} + \sqrt{2})}{(\sqrt{5} - \sqrt{2}) . (\sqrt{5} + \sqrt{2})}$ $= \frac{\sqrt{2} . (\sqrt{5} + \sqrt{2})}{{(\sqrt{5})}^{2} - {(\sqrt{2})}^{2}}$ $= \frac{\sqrt{2} . (\sqrt{5} + \sqrt{2})}{5 - 2}$ $= \frac{\sqrt{2} . (\sqrt{5} + \sqrt{2})}{3}$

Thực hành 2 trang 54 Toán 9 Tập 1: Khử mẫu của các biểu thức lấy căn:

a) $\sqrt{\frac{11}{6}}$

b) $a \sqrt{\frac{2}{5 a}}$ với a > 0

c) $4 x \sqrt{\frac{3}{4 x y}}$ với x > 0; y > 0

Lời giải:

a) $\sqrt{\frac{11}{6}} = \sqrt{\frac{11.6}{6.6}} = \frac{\sqrt{66}}{\sqrt{6^{2}}} = \frac{\sqrt{66}}{6}$

b) $a \sqrt{\frac{2}{5 a}} = a . \sqrt{\frac{2.5 a}{5 a .5 a}} = a \frac{\sqrt{10 a}}{\sqrt{{(5 a)}^{2}}} = a \frac{\sqrt{10 a}}{5 | a |}$ với a > 0

c) $4 x \sqrt{\frac{3}{4 x y}} = 4 x \sqrt{\frac{3.4 x y}{4 x y .4 x y}} = 4 x \frac{\sqrt{12 x y}}{\sqrt{{(4 x y)}^{2}}} = \frac{8 x \sqrt{3 x y}}{| 4 x y |}$ với x > 0; y > 0

Vận dụng 1 trang 54 Toán 9 Tập 1: Biết rằng hình thang và hình chữ nhật ở Hình 2 có diện tích bằng nhau. Tính chiều cao h của hình thang.

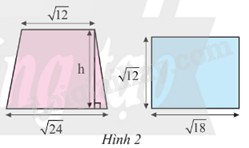
Giải SGK Toán 9 Bài 4 (Chân trời sáng tạo): Biến đổi đơn giản biểu thức chứa căn thức bậc hai (ảnh 4)

Lời giải:

Ta có diện tích hình chữ nhật là: $\sqrt{12} . \sqrt{18} = \sqrt{12.18} = \sqrt{216} = 6 \sqrt{6}$

Ta có diện tích hình thang bằng diện tích hình chữ nhật là: $6 \sqrt{6}$

Mà diện tích hình thang là: $\frac{1}{2} (\sqrt{12} + \sqrt{24}) . h$ = $6 \sqrt{6}$

Suy ra h = $\frac{2.6 \sqrt{6}}{(\sqrt{12} + \sqrt{24})} = 12 - 6 \sqrt{2}$

2. Rút gọn biểu thức chứa căn thức bậc hai

Hoạt động khám phá 2 trang 54 Toán 9 Tập 1: Hình vuông ABCD được chia thành hai hình vuông và hai hình chữ nhật như Hình 3.

a) Tính độ dài đường chéo của hai hình vuông AMIN và CEIF.

b) Tính độ dài đường chéo của hai hình vuông ABCD theo hai cách khác nhau.

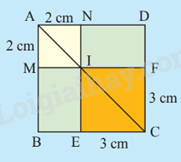
Giải SGK Toán 9 Bài 4 (Chân trời sáng tạo): Biến đổi đơn giản biểu thức chứa căn thức bậc hai (ảnh 5)

Lời giải:

a) Xét tam giác vuông AMI có AI = $\sqrt{2^{2} + 2^{2}} = 2 \sqrt{2}$ cm

Vậy độ dài đường chéo AMIN bằng $2 \sqrt{2}$ cm

Xét tam giác vuông IFC có IC = $\sqrt{3^{2} + 3^{2}} = 3 \sqrt{2}$ cm

Vậy độ dài đường chéo AMIN bằng $3 \sqrt{2}$ cm.

b) Cách 1:

Ta có: độ dài đường chéo ABCD = độ dài đường chéo AMNI + độ dài đường chéo IFCE = $2 \sqrt{2}$ + $3 \sqrt{2}$ = $5 \sqrt{2}$ cm.

Cách 2:

Độ dài cạnh AB là : 2 + 3 = 5 cm

Độ dài cạnh BC là : 2 + 3 = 5 cm

Xét tam giác vuông ABC có: AC = $\sqrt{A B^{2} + B C^{2}} = \sqrt{5^{2} + 5^{2}} = 5 \sqrt{2}$ cm.

Vậy độ dài đường chéo của hình vuông ABCD là $5 \sqrt{2}$ cm.

Thực hành 3 trang 55 Toán 9 Tập 1: Rút gọn các biểu thức sau:

a) $\sqrt{20} - \sqrt{5}$

b) $\sqrt{32} - \sqrt{18} + \frac{4}{\sqrt{2}}$

c) $(2 - \sqrt{10}) (2 - \sqrt{5})$

Lời giải:

a) $\sqrt{20} - \sqrt{5} = \sqrt{2^{2} .5} - \sqrt{5} = 2 \sqrt{5} - \sqrt{5} = \sqrt{5}$

b) $\sqrt{32} - \sqrt{18} + \frac{4}{\sqrt{2}}$ $= \sqrt{16.2} - \sqrt{9.2} + \frac{4}{\sqrt{2}}$ $= 4 \sqrt{2} - 3 \sqrt{2} + \frac{4}{\sqrt{2}}$ $= \sqrt{2} + \frac{4}{\sqrt{2}}$ $= \sqrt{2} . \sqrt{2} + 4$ $= 2 + 4 = 6$

c) $(2 - \sqrt{10}) (2 - \sqrt{5})$ $= 4 - 2 \sqrt{5} - 2 \sqrt{10} + \sqrt{10} . \sqrt{5}$ $= 4 - 2 \sqrt{5} + (\sqrt{5} - 2) \sqrt{10}$

Thực hành 4 trang 56 Toán 9 Tập 1: Rút gọn các biểu thức sau:

a) $\frac{2}{3} \sqrt{9 x^{3}} + 4 x \sqrt{\frac{x}{4}} - x^{2} \sqrt{\frac{1}{x}}$ với x > 0

b) $\frac{a^{2} - 5}{a + \sqrt{15}}$ với a $\neq - \sqrt{5}$

Lời giải:

a) $\frac{2}{3} \sqrt{9 x^{3}} + 4 x \sqrt{\frac{x}{4}} - x^{2} \sqrt{\frac{1}{x}}$

$\begin{array}{l} = \frac{2}{3} .3 \sqrt{x^{2} . x} + 4 x . \frac{1}{2} \sqrt{x} - \sqrt{x^{4} \frac{1}{x}} \\ = 2 x \sqrt{x} + 2 x \sqrt{x} - \sqrt{x^{3}} \\ = 4 x \sqrt{x} - x \sqrt{x} \\ = 3 x \sqrt{x} \end{array}$

b) $\frac{a^{2} - 5}{a + \sqrt{5}}$ với a $\neq - \sqrt{5}$

$\frac{a^{2} - 5}{a + \sqrt{5}} = \frac{(a + \sqrt{5}) (a - \sqrt{5})}{a + \sqrt{5}} = a - \sqrt{5}$

Vận dụng 2 trang 56 Toán 9 Tập 1: Trả lời câu hỏi trong hoạt động khởi động trang 52.

Một khu đất hình tam giác vuông tiếp giáp với hai thửa ruộng hình vuông có diện tích như hình bên. Khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé không? Kiểm tra bằng cách nào?

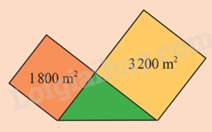
Giải SGK Toán 9 Bài 4 (Chân trời sáng tạo): Biến đổi đơn giản biểu thức chứa căn thức bậc hai (ảnh 6)

Lời giải:

Cạnh thửa ruộng bé hình vuông là: $\sqrt{1800} = 30 \sqrt{2}$ m.

Chu vi thửa ruộng bé là: $30 \sqrt{2} .4 = 120 \sqrt{2}$ m

Cạnh thửa ruộng lớn hình vuông là: $\sqrt{3200} = 40 \sqrt{2}$ m

Cạnh của tam giác vuông là: $\sqrt{{(30 \sqrt{2})}^{2} + {(40 \sqrt{2})}^{2}} = 50 \sqrt{2}$ m

Chu vi tam giác vuông là: $30 \sqrt{2} + 40 \sqrt{2} + 50 \sqrt{2} = 120 \sqrt{2}$ m.

Vậy khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé.

Bài tập

Bài 1 trang 56 Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau:

a) $\frac{2 \sqrt{5}}{\sqrt{2}}$

b) $\frac{10}{3 \sqrt{5}}$

c) $- \frac{3 \sqrt{a}}{\sqrt{12} a}$ với a > 0

Lời giải:

a) $\frac{2 \sqrt{5}}{\sqrt{2}} = \frac{2 \sqrt{5} . \sqrt{2}}{\sqrt{2} . \sqrt{2}} = \frac{2 \sqrt{10}}{2} = \sqrt{10}$

b) $\frac{10}{3 \sqrt{5}} = \frac{10. \sqrt{5}}{3 \sqrt{5} . \sqrt{5}} = \frac{10 \sqrt{5}}{15} = \frac{2 \sqrt{5}}{3}$

c) $- \frac{3 \sqrt{a}}{\sqrt{12} a} = - \frac{3 \sqrt{a} . \sqrt{12}}{\sqrt{12} a . \sqrt{12}} = \frac{6 \sqrt{3 a}}{12 a} = \frac{\sqrt{3 a}}{2 a}$ với a > 0

Bài 2 trang 56 Toán 9 Tập 1: Khử mẫu của biểu thức lấy căn:

a) $\sqrt{\frac{4}{7}}$

b) $\sqrt{\frac{5}{24}}$

c) $\sqrt{\frac{2}{3 a^{3}}}$ với a > 0

d) $2 a b \sqrt{\frac{a^{2}}{2 b}}$ với a < 0, b > 0

Lời giải:

a) $\sqrt{\frac{4}{7}} = \sqrt{\frac{4.7}{7.7}} = \frac{\sqrt{28}}{7}$

b) $\sqrt{\frac{5}{24}} = \sqrt{\frac{5.24}{24.24}} = \frac{\sqrt{120}}{24} = \frac{2 \sqrt{30}}{24} = \frac{\sqrt{30}}{12}$

c) $\sqrt{\frac{2}{3 a^{3}}} = \sqrt{\frac{2.3 a^{3}}{3 a^{3} .3 a^{3}}} = \frac{\sqrt{6 a^{3}}}{3 | a^{3} |}$ với a > 0

d) $2 a b \sqrt{\frac{a^{2}}{2 b}} = 2 a b \sqrt{\frac{a^{2} .2 b}{2 b .2 b}} = 2 a b \frac{\sqrt{2 b} | a |}{2 | b |} = - a^{2} \sqrt{2 b}$ với a < 0, b > 0

Bài 3 trang 56 Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau:

a) $\frac{4}{\sqrt{13} - 3}$

b) $\frac{10}{5 + 2 \sqrt{5}}$

c) $\frac{\sqrt{a} - \sqrt{b}}{\sqrt{a} + \sqrt{b}}$ với a > 0; b > 0, $a \neq b$ .

Lời giải:

a) $\frac{4}{\sqrt{13} - 3}$ $= \frac{4. (\sqrt{13} + 3)}{(\sqrt{13} - 3) (\sqrt{13} + 3)}$ $= \frac{4. (\sqrt{13} + 3)}{{(\sqrt{13})}^{2} - 3^{2}}$ $= \frac{4. (\sqrt{13} + 3)}{13 - 9}$ $= (\sqrt{13} + 3)$

b) $\frac{10}{5 + 2 \sqrt{5}}$ $= \frac{10. (5 - 2 \sqrt{5})}{(5 + 2 \sqrt{5}) (5 - 2 \sqrt{5})}$ $= \frac{10. (5 - 2 \sqrt{5})}{5^{2} - {(2 \sqrt{5})}^{2}}$ $= \frac{10. (5 - 2 \sqrt{5})}{5}$ $= 2 (5 - 2 \sqrt{5})$

c) $\frac{\sqrt{a} - \sqrt{b}}{\sqrt{a} + \sqrt{b}}$ $= \frac{(\sqrt{a} - \sqrt{b}) (\sqrt{a} - \sqrt{b})}{(\sqrt{a} + \sqrt{b}) (\sqrt{a} - \sqrt{b})}$ $= \frac{{(\sqrt{a} - \sqrt{b})}^{2}}{{(\sqrt{a})}^{2} - {(\sqrt{b})}^{2}}$ $= \frac{{(\sqrt{a} - \sqrt{b})}^{2}}{a - b}$ với a > 0; b > 0, $a \neq b$ .

Bài 4 trang 56 Toán 9 Tập 1: Rút gọn các biểu thức sau:

a) $2 \sqrt{3} - \sqrt{27}$

b) $\sqrt{45} - \sqrt{20} + \sqrt{5}$

c) $\sqrt{64 a} - \sqrt{18} - a \sqrt{\frac{9}{a}} + \sqrt{50}$ với a > 0

Lời giải:

a) $2 \sqrt{3} - \sqrt{27}$ $= 2 \sqrt{3} - \sqrt{9.3}$ $= 2 \sqrt{3} - 3 \sqrt{3}$ $= - \sqrt{3}$

b) $\sqrt{45} - \sqrt{20} + \sqrt{5}$ $= \sqrt{5.9} - \sqrt{4.5} + \sqrt{5}$ $= 3 \sqrt{5} - 2 \sqrt{5} + \sqrt{5}$ $= 2 \sqrt{5}$

c) $\sqrt{64 a} - \sqrt{18} - a \sqrt{\frac{9}{a}} + \sqrt{50}$ với a > 0

$\begin{array}{l} = 8 \sqrt{a} - \sqrt{2.9} - 3 \sqrt{\frac{a^{3}}{a}} + \sqrt{25.2} \\ = 8 \sqrt{a} - 3 \sqrt{2} - 3 a + 5 \sqrt{2} \\ = 8 \sqrt{a} + 2 \sqrt{2} - 3 a \end{array}$

Bài 5 trang 56 Toán 9 Tập 1: Tính

a) $(\sqrt{\frac{4}{3}} + \sqrt{3}) \sqrt{6}$

b) $\sqrt{18} : \sqrt{6} + \sqrt{8} . \sqrt{\frac{27}{2}}$

c) ${(1 - 2 \sqrt{5})}^{2}$

Lời giải:

a) $(\sqrt{\frac{4}{3}} + \sqrt{3}) \sqrt{6} = \sqrt{\frac{4}{3}} . \sqrt{6} + \sqrt{3} . \sqrt{6}$ $= \sqrt{\frac{24}{3}} + \sqrt{18}$ $= \sqrt{8} + \sqrt{18}$ $= \sqrt{2.4} + \sqrt{2.9}$ $= 2 \sqrt{2} + 3 \sqrt{2}$ $= 5 \sqrt{2}$

b) $\sqrt{18} : \sqrt{6} + \sqrt{8} . \sqrt{\frac{27}{2}}$ $= \sqrt{\frac{18}{6}} + \sqrt{8. \frac{27}{2}}$ $= \sqrt{3} + \sqrt{108}$ $= \sqrt{3} + \sqrt{36.3}$ $= \sqrt{3} + 6 \sqrt{3}$ $= 7 \sqrt{3}$

c) ${(1 - 2 \sqrt{5})}^{2} = 1 - 4 \sqrt{5} + 20 = 21 - 4 \sqrt{5}$

Bài 6 trang 56 Toán 9 Tập 1: Chứng minh rằng:

a) $\frac{a \sqrt{b} - b \sqrt{a}}{\sqrt{a b}} : \frac{1}{\sqrt{a} + \sqrt{b}} = a - b$ với a > 0; b > 0

b) $(1 + \frac{a + \sqrt{a}}{\sqrt{a} + 1}) (1 - \frac{a - \sqrt{a}}{\sqrt{a} - 1}) = 1 - a$ với a $\geq$ 0 và a $\neq$ 1

Lời giải:

a) $\frac{a \sqrt{b} - b \sqrt{a}}{\sqrt{a b}} : \frac{1}{\sqrt{a} + \sqrt{b}} = a - b$ với a > 0; b > 0

Xét vế trái ta có:

$\frac{a \sqrt{b} - b \sqrt{a}}{\sqrt{a b}} . (\sqrt{a} + \sqrt{b}) = \frac{(a \sqrt{b} - b \sqrt{a}) (\sqrt{a} + \sqrt{b})}{\sqrt{a b}}$

$= \frac{a \sqrt{a b} + a b - a b - b \sqrt{a b}}{\sqrt{a b}} = \frac{(a - b) \sqrt{a b}}{\sqrt{a b}} = a - b$ = VP

b) $(1 + \frac{a + \sqrt{a}}{\sqrt{a} + 1}) (1 - \frac{a - \sqrt{a}}{\sqrt{a} - 1}) = 1 - a$ với a $\geq$ 0 và a $\neq$ 1

Xét vế trái ta có:

$(1 + \frac{a + \sqrt{a}}{\sqrt{a} + 1}) (1 - \frac{a - \sqrt{a}}{\sqrt{a} - 1}) = (1 + \frac{\sqrt{a} (\sqrt{a} + 1)}{\sqrt{a} + 1}) (1 - \frac{\sqrt{a} (\sqrt{a} - 1)}{\sqrt{a} - 1})$

$= (1 + \sqrt{a}) (1 - \sqrt{a}) = 1 - {(\sqrt{a})}^{2} = 1 - a$ = VP.

Bài 7 trang 56 Toán 9 Tập 1: Tam giác ABC được vẽ trên ô vuông như Hình 4. Tính diện tích và chu vi của tam giác ABC

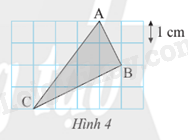
Giải SGK Toán 9 Bài 4 (Chân trời sáng tạo): Biến đổi đơn giản biểu thức chứa căn thức bậc hai (ảnh 7)

Lời giải:

Ta có: AB = 2cm; BC = 4cm; AC = 5cm

Chu vi tam giác ABC là: 2 + 4 + 5 = 11 cm

Diện tích tam giác ABC là: $\frac{1}{2} A B . B C$ = $\frac{1}{2} .2 .4 = 4$ cm²

Bài 8 trang 56 Toán 9 Tập 1: Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5. Tính chu vi của vườn hoa đó.

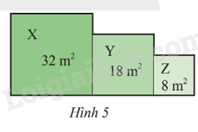
Giải SGK Toán 9 Bài 4 (Chân trời sáng tạo): Biến đổi đơn giản biểu thức chứa căn thức bậc hai (ảnh 8)

Lời giải:

Ta có cạnh hình vuông X là: $\sqrt{32} = 4 \sqrt{2}$ m

Suy ra chu vi hình vuông X là: $4 \sqrt{2} .4 = 16 \sqrt{2}$ m

Ta có cạnh hình vuông Y là: $\sqrt{18} = 3 \sqrt{2}$ m

Suy ra chu vi hình vuông Y là: $3 \sqrt{2} .4 = 12 \sqrt{2}$ m

Ta có cạnh hình vuông Z là: $\sqrt{8} = 2 \sqrt{2}$ m

Suy ra chu vi hình vuông Z là: $2 \sqrt{2} .4 = 8 \sqrt{2}$ m

Vậy chu vi của vườn hoa đó là: $16 \sqrt{2} + 12 \sqrt{2} + 8 \sqrt{2} = 36 \sqrt{2}$ m.

Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Bài 3. Tính chất của phép khai phương

Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Bài tập cuối chương 3

Bài 1. Tỉ số lượng giác của góc nhọn

Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông

Bài tập cuối chương 4

Lý thuyết Biến đổi đơn giản biểu thức chứa căn thức bậc hai

1. Trục căn thức ở mẫu

- Với các biểu thức A và B thỏa mãn $A B \geq 0, B \neq 0$ , ta có:

$\sqrt{\frac{A}{B}} = \sqrt{\frac{A B}{B^{2}}} = \frac{\sqrt{A B}}{\sqrt{B^{2}}} = \frac{\sqrt{A B}}{| B |}$ .

- Với các biểu thức A, B và B > 0, ta có $\frac{A}{\sqrt{B}} = \frac{A \sqrt{B}}{B}$ .

- Với các biểu thức A, B, C mà $A \geq 0, A \neq B^{2}$ , ta có:

$\frac{C}{\sqrt{A} + B} = \frac{C (\sqrt{A} - B)}{A - B^{2}}; \frac{C}{\sqrt{A} - B} = \frac{C (\sqrt{A} + B)}{A - B^{2}}$ .

- Với các biểu thức A, B, C mà $A \geq 0, B \geq 0, A \neq B$ , ta có:

$\frac{C}{\sqrt{A} + \sqrt{B}} = \frac{C (\sqrt{A} - \sqrt{B})}{A - B}; \frac{C}{\sqrt{A} - \sqrt{B}} = \frac{C (\sqrt{A} + \sqrt{B})}{A - B}$ .

Ví dụ:

$\frac{2}{3 \sqrt{5}} = \frac{2 \sqrt{5}}{3 {(\sqrt{5})}^{2}} = \frac{2 \sqrt{5}}{3.5} = \frac{2 \sqrt{5}}{15}$ ;

$\frac{a}{3 - 2 \sqrt{2}} = \frac{a (3 + 2 \sqrt{2})}{(3 - 2 \sqrt{2}) . (3 + 2 \sqrt{2})} = \frac{a (3 + 2 \sqrt{2})}{3^{2} - {(2 \sqrt{2})}^{2}} = \frac{a (3 + 2 \sqrt{2})}{9 - 8} = (3 + 2 \sqrt{2}) a$ .

2. Rút gọn biểu thức chứa căn thức bậc hai

Để rút gọn biểu thức có chứa căn thức bậc hai, ta cần vận dụng thích hợp các tính chất (giao hoán, kết hợp, phân phối) của các phép tính, quy tắc về thứ tự thực hiện và phép biến đổi đã biết.

Ví dụ:

$\begin{array}{l} A = 2 \sqrt{3} - \sqrt{75} + \sqrt{{(1 - \sqrt{3})}^{2}} \\ = 2 \sqrt{3} - \sqrt{{3.5}^{2}} + | 1 - \sqrt{3} | \\ = 2 \sqrt{3} - 5 \sqrt{3} + \sqrt{3} - 1 \\ = - 1 - 2 \sqrt{3} \end{array}$

$\begin{array}{l} B = x \sqrt{x} - \frac{x^{2} - x}{\sqrt{x} + 1} \\ = x \sqrt{x} - \frac{(x^{2} - x) (\sqrt{x} - 1)}{(\sqrt{x} + 1) (\sqrt{x} - 1)} \\ = x \sqrt{x} - \frac{x (x - 1) (\sqrt{x} - 1)}{(\sqrt{x} + 1) (\sqrt{x} - 1)} \\ = x \sqrt{x} - \frac{x (x - 1) (\sqrt{x} - 1)}{x - 1} \\ = x \sqrt{x} - x (\sqrt{x} - 1) \\ = x \sqrt{x} - x \sqrt{x} + x \\ = x \end{array}$