Biết rằng hình A và hình vuông B trong Hình 2 có diện tích bằng nhau. Tính độ dài cạnh x

Trịnh Thị Thu Hiền Ngày: 27-07-2024 Lớp 9
188
188

Với giải Vận dụng 1 trang 39 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Căn bậc hai giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 1: Căn bậc hai

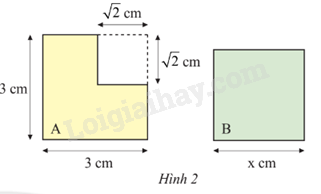
Vận dụng 1 trang 39 Toán 9 Tập 1: Biết rằng hình A và hình vuông B trong Hình 2 có diện tích bằng nhau. Tính độ dài cạnh x của hình vuông B.

Giải SGK Toán 9 Bài 1 (Chân trời sáng tạo): Căn bậc hai (ảnh 2)

Lời giải:

Xét hình A:

Ta có diện tích cả hình vuông cạnh 3cm là : 3.3 = 9 cm2

Ta có diện tích cả hình vuông cạnh 2 cm là : 2. 2 = 2 cm2

Suy ra diện tích hình A là: 9 – 2 = 7 cm2

Mà hình vuông B bằng diện tích hình A là 7 cm2

Nên x.x = x2 = 7 suy ra x = 7 cm.

Lý Thuyết Căn bậc hai

Khái niệm căn bậc hai

Cho số thực a không âm. Số thực x thỏa mãn x2=a được gọi là một căn bậc hai của a.

Chú ý:

- Mỗi số dương a có đúng hai căn bậc hai là hai số đối nhau: số dương là a (căn bậc hai số học của a) và số âm là −a.

- Số 0 chỉ có đúng một căn bậc hai là chính nó, ta viết 0=0.

- Số âm không có căn bậc hai.

- Phép toán tìm căn bậc hai số học của số không âm gọi là phép khai căn bậc hai hay phép khai phương (gọi tắt là khai phương).

­- Nếu a>b>0 thì a>b. Suy ra −a<−b<0<b<a.

Ví dụ:

  • 81=9 nên 81 có hai căn bậc hai là 9 và -9.
  • Căn bậc hai số học của 121 là 121=11.
 

 

Xem thêm lời giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Vận dụng 1 trang 39 Toán 9 Tập 1: Biết rằng hình A và hình vuông B trong Hình 2 có diện tích bằng nhau. Tính độ dài cạnh x của hình vuông B......

Thực hành 6 trang 39 Toán 9 Tập 1: Sử dụng máy tính cầm tay để:.....

Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 2

Bài 1. Căn bậc hai

Bài 2. Căn bậc ba

Bài 3. Tính chất của phép khai phương

Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Bài tập cuối chương 3

Xem thêm các nội dung khác:

Đánh giá

0

0 đánh giá

Đánh giá
Bài viết cùng môn học
Toán Tổng hợp kiến thức
Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6
Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My
169
Toán Tổng hợp kiến thức
Tìm các tập hợp Ư(8); Ư(12); Ư(15)
Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My
143
Toán Tổng hợp kiến thức
Tìm BCNN của 84 và 108
Tìm BCNN của 84 và 108 Lữ Ngọc My My
115
Toán Tổng hợp kiến thức
Cho biết cos∝ = 12/13 giá trị của tan ∝ là
Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My
116

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.

DMCA.com Protection Status