20 Bài tập Ba trường hợp đồng dạng của hai tam giác lớp 8 (sách mới) có đáp án

Van Anh Ngày: 21-08-2024 Lớp 8

Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Ba trường hợp đồng dạng của hai tam giác được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Ba trường hợp đồng dạng của hai tam giác . Mời các bạn đón xem:

Bài tập Toán 8 Ba trường hợp đồng dạng của hai tam giác

A. Bài tập Ba trường hợp đồng dạng của hai tam giác

Bài 1: Cho tam giác ABC có AB = 6cm; AC = 9cm; BC = 12cm và tam giác MNP có NP = 8cm; MN= 12cm; PM = 16cm. khẳng định nào sau đây là đúng?

A.
$Δ A B C ∽ Δ M N P$
B.
$Δ A B C ∽ Δ N M P$
C.
$Δ A B C ∽ Δ N P M$
D.
$Δ B A C ∽ Δ M N P$

Hướng dẫn giải:

Đáp án : C

Vì $\frac{A B}{N P} = \frac{6}{8} = \frac{3}{4}; \frac{A C}{N M} = \frac{9}{12} = \frac{3}{4}; \frac{B C}{P M} = \frac{12}{16} = \frac{3}{4}$

Nên $\frac{A B}{N P} = \frac{A C}{N M} = \frac{B C}{P M} = \frac{3}{4} \Rightarrow Δ A B C ∽ Δ N P M$

Bài 2: Cho tam giác ABC có AB = 3cm, AC = 5cm; BC = 7cm và MNP có MN = 6cm; MP = 10cm; NP = 14cm. Tỉ số chu vi của hai tam giác ABC và MNP là

A.
$\frac{3}{5}$ .
B.
2.
C.
$\frac{5}{6}$ .
D.
$\frac{1}{2}$ .

Hướng dẫn giải:

Đáp án : D

Vì $\frac{A B}{M N} = \frac{3}{6} = \frac{1}{2}; \frac{A C}{M P} = \frac{5}{10} = \frac{1}{2}; \frac{B C}{N P} = \frac{7}{14} = \frac{1}{2}$

Suy ra: $\frac{A B}{M N} = \frac{A C}{M P} = \frac{B C}{N P} = \frac{1}{2} \Rightarrow Δ A B C ∽ Δ M N P$ theo tỉ số đồng dạng là $\frac{1}{2}$

Vì $\frac{A B}{M N} = \frac{A C}{M P} = \frac{B C}{N P} = \frac{A B + A C + B C}{M N + M P + N P} = \frac{1}{2}$

$\Rightarrow \frac{C V_{Δ A B C}}{C V_{Δ M N P}} = \frac{1}{2}$

Bài 3: Cho tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với $4 : 5 : 6$ . Cho biết $Δ A B C ∽ Δ A^{'} B^{'} C^{'}$ và cạnh nhỏ nhất của $Δ A^{'} B^{'} C^{'}$ bằng 2cm. Độ dài các cạnh còn lại của tam giác $A^{'} B^{'} C^{'}$ lần lượt là

A.
3cm; 4cm
B.
2,5cm; 4cm.
C.
3cm; 2cm
D.
2,5cm; 3cm.

Hướng dẫn giải:

Đáp án : D

Theo đầu bài tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với $4 : 5 : 6$

Và $Δ A B C ∽ Δ A^{'} B^{'} C^{'}$ nên $Δ A^{'} B^{'} C^{'}$ cũng có độ dài các cạnh tỉ lệ với $4 : 5 : 6$

Giả sử $A^{'} B^{'} < A^{'} C^{'} < B^{'} C^{'} \Rightarrow A^{'} B^{'} = 2 c m$

$\Rightarrow \frac{A^{'} B^{'}}{4} = \frac{A^{'} C^{'}}{5} = \frac{B^{'} C^{'}}{6} \Rightarrow \frac{A^{'} C^{'}}{5} = \frac{B^{'} C^{'}}{6} = \frac{2}{4}$

$\begin{array}{l} \Rightarrow A^{'} C^{'} = \frac{5.2}{4} = 2, 5 (c m) \\ \Rightarrow B^{'} C^{'} = \frac{6.2}{4} = 3 (c m) \end{array}$

Độ dài các cạnh còn lại của tam giác A’B’C’ lần lượt là 2,5cm ; 3cm.

Bài 4: Cho $Δ A B C ∽ Δ A_{1} B_{1} C_{1}$ khẳng định nào sau đây là sai

A.
$\frac{A B}{A_{1} B_{1}} = \frac{A C}{A_{1} C_{1}} = \frac{B C}{B_{1} C_{1}}$ .
B.
$\frac{A_{1} B_{1}}{A B} = \frac{A_{1} C_{1}}{A C} = \frac{B_{1} C_{1}}{B C}$ .
C.
$\frac{B_{1} C_{1}}{B C} = \frac{A_{1} C_{1}}{A C} = \frac{A_{1} B_{1}}{A B}$ .
D.
$\frac{A B}{A_{1} B_{1}} = \frac{A_{1} C_{1}}{A C} = \frac{B C}{B_{1} C_{1}}$ .

Hướng dẫn giải:

Đáp án : D

$Δ A B C ∽ Δ A_{1} B_{1} C_{1}$ $\Rightarrow \frac{A B}{A_{1} B_{1}} = \frac{A C}{A_{1} C_{1}} = \frac{B C}{B_{1} C_{1}}$ (các cạnh tương ứng)

$\Rightarrow \frac{A_{1} B_{1}}{A B} = \frac{A_{1} C_{1}}{A C} = \frac{B_{1} C_{1}}{B C}$ (Tính chất tỉ lệ thức)

$\Rightarrow \frac{B_{1} C_{1}}{B C} = \frac{A_{1} C_{1}}{A C} = \frac{A_{1} B_{1}}{A B}$ (Tính chất tỉ lệ thức)

$\Rightarrow \frac{A B}{A_{1} B_{1}} = \frac{A_{1} C_{1}}{A C} = \frac{B C}{B_{1} C_{1}}$ là khẳng định sai

Bài 5: Cho $Δ A B C$ , có AC = 18cm; AB = 9cm; BC = 15cm. Trên cạnh AC lấy điểm N sao cho AN = 3cm, trên cạnh AB lấy điểm M sao cho AM = 6cm. Tính độ dài đoạn thẳng MN:

A.
MN= 6cm
B.
MN = 5cm
C.
MN = 8cm
D.
MN = 9cm

Hướng dẫn giải:

Đáp án : B

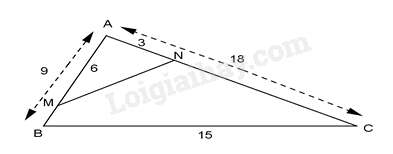
20 Bài tập Ba trường hợp đồng dạng của hai tam giác lớp 8 (sách mới) có đáp án (ảnh 1)

Ta có: $\frac{A N}{A B} = \frac{3}{9} = \frac{1}{3}, \frac{A M}{A C} = \frac{6}{18} = \frac{1}{3} \Rightarrow \frac{A N}{A B} = \frac{A M}{A C} = \frac{1}{3}$

Xét $Δ A N M$ và $Δ A B C$ có: $\frac{A N}{A B} = \frac{A M}{A C} (c m t); \hat{A}$ chung

$\begin{array}{l} \Rightarrow Δ A N M ∽ Δ A B C (c - g - c) \\ \Rightarrow \frac{A N}{A B} = \frac{A M}{A C} = \frac{M N}{C B} = \frac{1}{3} \Rightarrow \frac{M N}{15} = \frac{1}{3} \Rightarrow M N = \frac{15}{3} = 5 (c m) . \end{array}$

B. Lý thuyết Ba trường hợp đồng dạng của hai tam giác

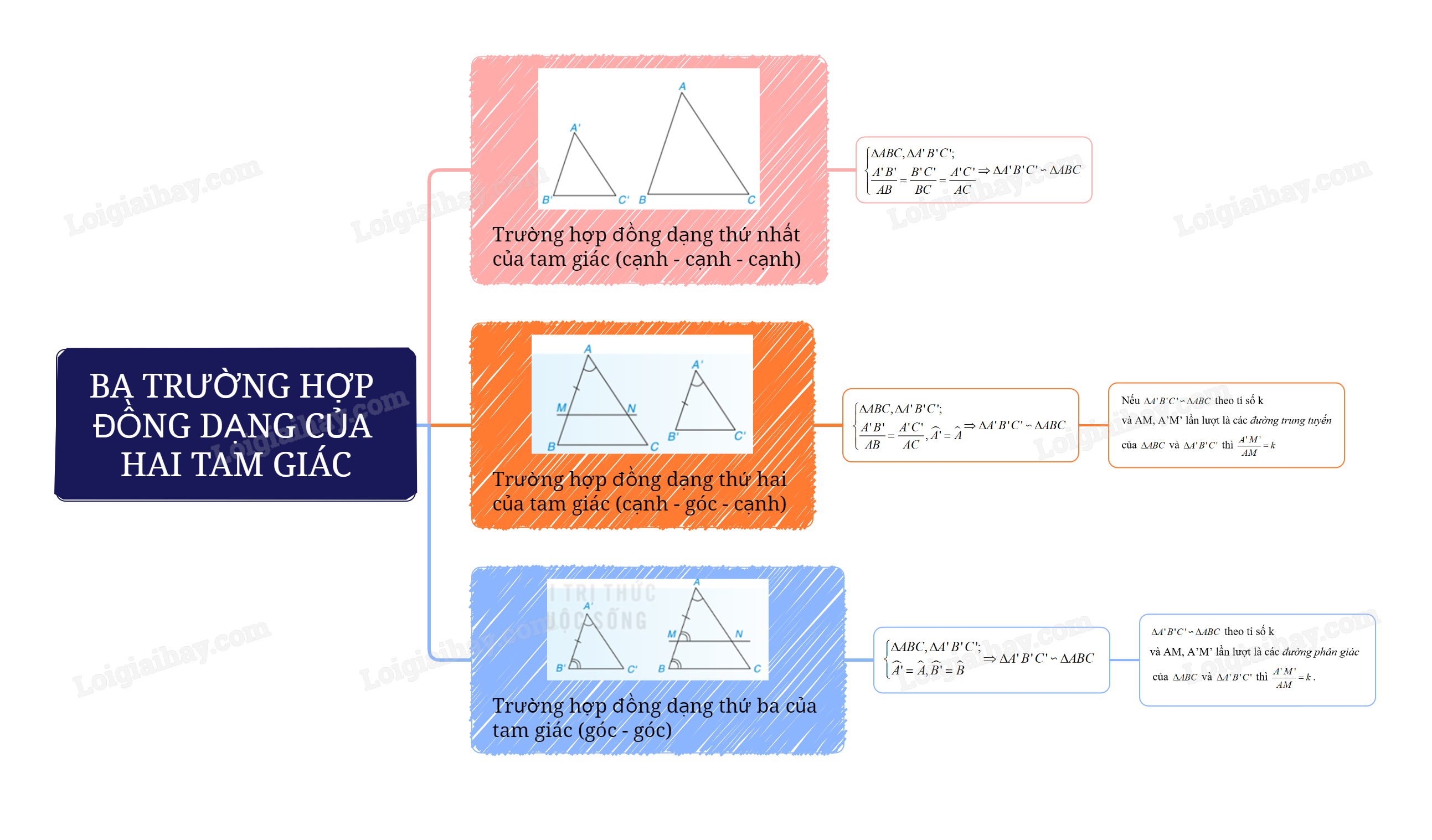
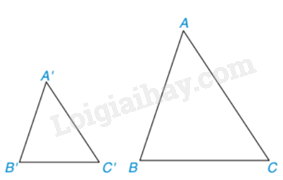
1. Trường hợp đồng dạng thứ nhất của tam giác

Trường hợp đồng dạng cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.

${\begin{cases} Δ A B C, Δ A^{'} B^{'} C^{'}; \\ \frac{A^{'} B^{'}}{A B} = \frac{B^{'} C^{'}}{B C} = \frac{A^{'} C^{'}}{A C} \end{cases} \Rightarrow Δ A^{'} B^{'} C^{'} ∽ Δ A B C$

Lý thuyết Ba trường hợp đồng dạng của hai tam giác (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

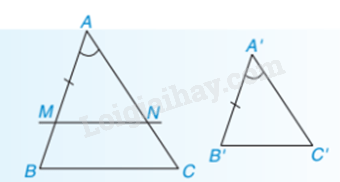
2. Trường hợp đồng dạng thứ hai của tam giác

Trường hợp đồng dạng cạnh – góc – cạnh:

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.

${\begin{cases} Δ A B C, Δ A^{'} B^{'} C^{'}; \\ \frac{A^{'} B^{'}}{A B} = \frac{A^{'} C^{'}}{A C}, \hat{A^{'}} = \hat{A} \end{cases} \Rightarrow Δ A^{'} B^{'} C^{'} ∽ Δ A B C$

Lý thuyết Ba trường hợp đồng dạng của hai tam giác (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 2)

Nhận xét: Nếu $Δ A^{'} B^{'} C^{'} ∽ Δ A B C$ theo tỉ số k và AM, A’M’ lần lượt là các đường trung tuyến của $Δ A B C$ và $Δ A^{'} B^{'} C^{'}$ thì $\frac{A^{'} M^{'}}{A M} = k$

3. Trường hợp đồng dạng thứ ba của tam giác

Trường hợp đồng dạng góc – góc:

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

${\begin{cases} Δ A B C, Δ A^{'} B^{'} C^{'}; \\ \hat{A^{'}} = \hat{A}, \hat{B^{'}} = \hat{B} \end{cases} \Rightarrow Δ A^{'} B^{'} C^{'} ∽ Δ A B C$

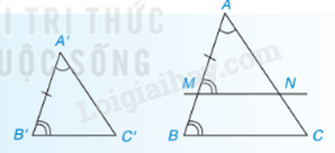
Lý thuyết Ba trường hợp đồng dạng của hai tam giác (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 3)

Nhận xét: $Δ A^{'} B^{'} C^{'} ∽ Δ A B C$ theo tỉ số k và AM, A’M’ lần lượt là các đường phân giác của $Δ A B C$ và $Δ A^{'} B^{'} C^{'}$ thì $\frac{A^{'} M^{'}}{A M} = k$