Với giải Bài 9* trang 60 SBT Toán lớp 8 Cánh diều chi tiết trong Bài 1: Định lí Thalès trong tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 1: Định lí Thalès trong tam giác
Bài 9* trang 60 SBT Toán 8 Tập 2: Cho tam giác ABC có ba góc nhọn, đường cao AH. Trên AH, AB, AC lần lượt lấy các điểm D, E, F sao cho . Chứng minh: EF // BC.
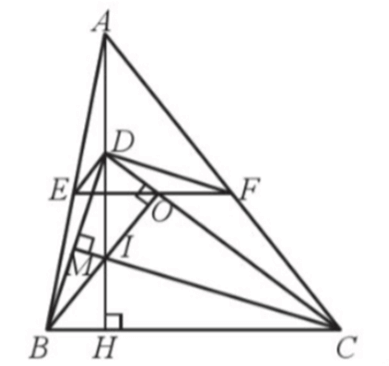
Lời giải:
Kẻ BO ⊥ CD, CM ⊥ BD, BO cắt CM tại I , suy ra D là trực tâm của ∆BIC hay DI ⊥ BC.
Mặt khác, AH ⊥ BC suy ra I, D, A thẳng hàng.
Do nên ED ⊥ DC, DF ⊥ DB
Ta có: ED ⊥ DC, BO ⊥ CD, I ∈ BO nên ED // BI;
DF ⊥ DB, CM ⊥ BD, I ∈ CM nên DF // CI.
Xét ∆ABI với DE // BI, ta có: (hệ quả của định lí Thalès)
Xét ∆ACI với DF // IC, ta có: (hệ quả của định lí Thalès)
Suy ra
Xét ∆ABC có nên EF// BC (định lí Thalès đảo).
Xem thêm lời giải sách bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:
Bài 1 trang 59 SBT Toán 8 Tập 2: Cho các đoạn thẳng AB = 6 cm, CD = 4 cm, PQ = 8 cm, EF = 10 cm, MN = 25 cm, RS = 15 cm. Tìm phát biểu đúng trong các phát biểu sau:....
Bài 2 trang 59 SBT Toán 8 Tập 2: Cho các đoạn thẳng EF = 6 cm, GH = 3 cm, IK = 5 cm, MN = x cm. Tìm x để hai đoạn thẳng EF và GH tỉ lệ với hai đoạn thẳng IK và MN....
Bài 3 trang 59 SBT Toán 8 Tập 2: Cho tam giác ABC. Một đường thẳng d song song với BC và cắt các cạnh AB, AC của tam giác đó lần lượt tại M, N với và AN + AC = 16 cm. Tính AN.....
Bài 4 trang 60 SBT Toán 8 Tập 2: Toà nhà Bitexco Financial (hay tháp tài chinh Bitexco) được xây dụng tại trung tâm Quận 1, Thành phố Hồ Chí Minh. Toà nhà có 68 tầng (không kể các tầng hầm). Biết rằng khi toà nhà có bóng MP in trên mặt đất dài 47,5 m, thì cùng thời điểm đó một cột cờ AB cao 12 m có bóng AP in trên mặt đất dài 2,12 m (Hình 8). Tính chiều cao MN của toà nhà theo đon vị mét (làm tròn kết quả đến hàng đơn vị)....
Bài 5 trang 60 SBT Toán 8 Tập 2: Cho tam giác ABC vuông ở A. Vẽ ra phía ngoài tam giác đó các tam giác BAD vuông cân ở B, ACF vuông cân ở C. Gọi H là giao điểm của AB và DC, K là giao điểm của AC và BF (Hình 9). Chứng minh:...
Bài 6 trang 60 SBT Toán 8 Tập 2: Trong Hình 10, cho biết ABCD là hình thang, AB // CD (AB < CD); M là trung điểm của DC; AM cắt BD ở I; BM cắt AC ở K; IK cắt AD, BC lần lượt ở E, F. Chứng minh:..
Bài 7 trang 60 SBT Toán 8 Tập 2: Cho ABCD là hình bình hành. Một đường thẳng d đi qua A cắt BD, BC, DC lần lượt tại E, K, G (Hình 11). Chứng minh:...
Bài 8 trang 60 SBT Toán 8 Tập 2: An có một mảnh bìa có dạng hình tam giác ABC nhưng bị rách. An muốn cắt bỏ phần bị rách với vết cắt là đoạn thẳng MN. Tính diện tích tứ giác MNCB theo diện tích tam giác ABC, biết và (Hình 12)...
Bài 9* trang 60 SBT Toán 8 Tập 2: Cho tam giác ABC có ba góc nhọn, đường cao AH. Trên AH, AB, AC lần lượt lấy các điểm D, E, F sao cho . Chứng minh: EF // BC......
Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác: