Cho hình chóp cụt tam giác đều ABC.A'B'C' có đường cao HH'=2a

Cho hình chóp cụt tam giác đều ABC.A'B'C' có đường cao HH'=2a

Van Anh Ngày: 19-11-2023 Lớp 11

688

Với giải Bài 9 trang 68 SBT Toán lớp 11 Chân trời sáng tạo chi tiết trong Bài 4: Khoảng cách trong không gian giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 4: Khoảng cách trong không gian

Bài 9 trang 68 SBT Toán 11 Tập 2: Cho hình chóp cụt tam giác đều $A B C . A^{'} B^{'} C^{'}$ có đường cao $H H^{'} = 2 a$ . Cho biết AB = 2a, $A^{'} B^{'} = a$ . Gọi B₁, C₁ lần lượt là trung điểm của AB, AC. Tính thể tích của:

a) Khối chóp cụt đều $A B C . A^{'} B^{'} C^{'}$ .

b) Khối lăng trụ $A B_{1} C_{1} . A^{'} B^{'} C^{'}$ .

Lời giải:

Cho hình chóp cụt tam giác đều ABC A'B'C' có đường cao HH' = 2a Cho biết AB = 2a

a)

Áp dụng công thức: $V = \frac{1}{3} h (S + \sqrt{S S'} + S')$ ,

Do ABC, A¢B¢C¢ là các tam giác đều nên: 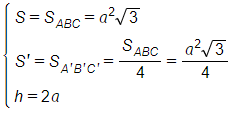Cho hình chóp cụt tam giác đều ABC A'B'C' có đường cao HH' = 2a Cho biết AB = 2a , thay vào công thức trên ta có:

$V = \frac{1}{3} . 2 a . (a^{2} \sqrt{3} + \sqrt{a^{2} \sqrt{3} . \frac{a^{2} \sqrt{3}}{4}} + \frac{a^{2} \sqrt{3}}{4})$

$= \frac{2}{3} a . (\frac{5 \sqrt{3} a^{2}}{4} + \sqrt{\frac{3 a^{4}}{4}})$ $= \frac{2}{3} a . (\frac{5 \sqrt{3} a^{2}}{4} + \frac{\sqrt{3} a^{2}}{2})$

$= \frac{2}{3} a . (\frac{5 \sqrt{3} a^{2}}{4} + \frac{\sqrt{3} a^{2}}{2}) = \frac{2}{3} a . \frac{7 \sqrt{3} a^{2}}{4} = \frac{7 a^{3} \sqrt{3}}{6}$ .

b)Áp dụng công thức: $V' = S' . h'$ , với $S' = \frac{a^{2} \sqrt{3}}{4}, h' = 2 a .$

Ta có: $V' = \frac{a^{2} \sqrt{3}}{4} .2 a . = \frac{a^{3} \sqrt{3}}{2}$ .

Xem thêm lời bài sách bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1 trang 68 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều canh a, cạnh bên SA vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, biết SA = $\frac{a \sqrt{6}}{2}$ ......

Bài 2 trang 68 SBT Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của SC...

Bài 3 trang 68 SBT Toán 11 Tập 2: Cho hình lập phương $A B C D . A^{'} B^{'} C^{'} D^{'}$ cạnh a. Gọi M, N lần lượt là trung điểm của AC và $B^{'} C^{'}$ . Tính khoảng cách giữa hai đường thẳng MN và $B^{'} D^{'}$ ....

Bài 4 trang 68 SBT Toán 11 Tập 2: Cho hình tứ diện đều ABCD có cạnh bằng $\sqrt{11}$ . Gọi I là trung điểm của cạnh CD. Tính khoảng cách giữa hai đường thẳng AC và BI....

Bài 5 trang 68 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có tam giác vuông cân tại B, AC = $a \sqrt{2}$ , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60°. Tính theo a thể tích V của khối chóp S.ABC....

Bài 6 trang 68 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) và SA = , đáy ABCD là hình thang vuông tại A và B có AB = a, AD = 3a, BC = a. Tính thể tích khối chóp S.BCD theo a....

Bài 7 trang 68 SBT Toán 11 Tập 2: Cho hình lăng trụ đều $A B C . A^{'} B^{'} C^{'}$ có cạnh đáy bằng a. Biết $d (A (A^{'} B C^{'})) = \frac{a \sqrt{57}}{12}$ . Tính $V_{A B C . A^{'} B^{'} C^{'}}$ ....

Bài 8 trang 68 SBT Toán 11 Tập 2: Một hình hộp chữ nhật $A B C D . A^{'} B^{'} C^{'} D^{'}$ có ba kích thước là 2 cm, 3 cm và 6 cm. Tính thể tích của khối tứ diện $A C B^{'} D^{'}$ .....

Bài 9 trang 68 SBT Toán 11 Tập 2: Cho hình chóp cụt tam giác đều $A B C . A^{'} B^{'} C^{'}$ có đường cao $H H^{'} = 2 a$ . Cho biết AB = 2a, $A^{'} B^{'} = a$ . Gọi B₁, C₁ lần lượt là trung điểm của AB, AC. Tính thể tích của:...

Bài 10 trang 68 SBT Toán 11 Tập 2: Tính thể tích một cái sọt đựng đồ có dạng hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 80 cm, đáy nhỏ có cạnh bằng 40 cm và cạnh bên bằng 80 cm....

Xem thêm các bài giải SBT Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Hai mặt phẳng vuông góc

Bài 4: Khoảng cách trong không gian

Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài tập cuối chương 8

Bài 1: Biến cố giao và quy tắc nhân xác suất

Bài 2: Biến cố hợp và quy tắc cộng xác suất

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

164

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

137

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.