Với lời giải SBT Toán 8 trang 79 Tập 1 Bài tập cuối chương 4 trang 78 sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài tập cuối chương 4 trang 78

Bài 19 trang 79 SBT Toán 8 Tập 1: Cho hình chóp tam giác đều có thể tích bằng $32\sqrt{3}c{m}^3$ và diện tích đáy bằng $4\sqrt{3}c{m}^2$. Tính chiều cao của hình chóp tam giác đều đó.

Lời giải:

Áp dụng công thức $V=\frac{1}{3}.S.h$, trong đó $V$ là thể tích $S$ là diện tích đáy, $h$ là chiều cao của hình chóp tam giác đều ta có: $32\sqrt{3}=\frac{1}{3}.4\sqrt{3}.h$

Suy ra $h=24\left(cm\right)$

Vậy chiều cao của hình chóp tam giác đều đó là 24 cm.

Bài 20 trang 79 SBT Toán 8 Tập 1: Cho hai hình chóp tam giác đều $S.ABC$ và $S^{\prime }.A^{\prime }{B}^{\prime }{C}^{\prime }$ lần lượt có độ dài cạnh đáy là $a$ và $a^{\prime }$, độ dài trung đoạn là $d$ và $d^{\prime }$. Tính tỉ số giữa $d$ và $d^{\prime }$, biết diện tích xung quanh của $S.ABC$ gấp $k$ lần diện tích xung quanh của $S^{\prime }.A^{\prime }{B}^{\prime }{C}^{\prime }\left(k\ne 0\right)$ và $a=2a^{\prime }$. Biết rằng $a,a^{\prime },d,d^{\prime }$ cùng đơn vị đo.

Lời giải:

Áp dụng công thức tính diện tích xung quanh của hình chóp tam giác đều $S_{xq}=\frac{1}{2}.C.d$, ta có:

Diện tích xung quanh của hình chóp tam giác đều $S.ABC$ là:

$\frac{1}{2}.\left(3a\right).d=\frac{1}{2}.3.2a^{\prime }.d=3a^{\prime }d$

Diện tích xung quanh của hình chóp tam giác đều $S^{\prime }.A^{\prime }{B}^{\prime }{C}^{\prime }$ là:

$\frac{1}{2}.\left(3a^{\prime }\right).d^{\prime }=\frac{3}{2}{a}^{\prime }{d}^{\prime }$

Do diện tích xung quanh của $S.ABC$ gấp $k$ lần diện tích xung quanh của $S^{\prime }.A^{\prime }{B}^{\prime }{C}^{\prime }$ nên $3a^{\prime }d=k.\frac{3}{2}{a}^{\prime }{d}^{\prime }$. Suy ra $\frac{d}{d^{\prime }}=\frac{k}{2}$.

Vậy tỉ số giữa $d$ và $d^{\prime }$ là $\frac{k}{2}$.

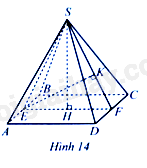
Bài 21 trang 79 SBT Toán 8 Tập 1: Cho hình chóp tứ giác đều $S.ABCD$ có chiều cao $SH$. Gọi $E,F$ lần lượt là trung điểm của $AB,CD$. Kẻ $EK$ vuông góc với $SF$ tại $K$ (Hình 14). Biết $AB=EF=13cm,SH=EK$. Tính tổng diện tích các mặt của hình chóp tứ giác đều đó.

Lời giải:

Ta có diện tích của tam giác $SEF$ bằng:

$\frac{1}{2}.SH.EF=\frac{1}{2}.EK.SF$

Mà $SH=EK$, suy ra $SF=EF=13cm$

Diện tích xung quanh của hình chóp tứ giác đều $S.ABCD$ là: $\frac{1}{2}.\left(13.4\right).13=338\left(c{m}^2\right)$

Diện tích đáy của hình chóp tứ giác đều $S.ABCD$ là: ${13}^2=169\left(c{m}^2\right)$

Tổng diện tích các mặt của hình chóp tứ giác đều $S.ABCD$ là: $338+169=507\left(c{m}^2\right)$.

Bài 22 trang 79 SBT Toán 8 Tập 1: Tính diện tích xung quanh của hình chóp tứ giác đều ở mỗi hình 15a, 15b:

Lời giải:

Áp dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều $S_{xq}=\frac{1}{2}.C.d$, ta có:

Diện tích xung quanh của hình chóp tứ giác đều ở hình 15a là:

$\frac{1}{2}.\left(6.4\right).5=60\left(c{m}^2\right)$

Diện tích xung quanh của hình chóp tứ giác đều ở hình 15b là:

$\frac{1}{2}.\left(10.4\right).13=260\left(c{m}^2\right)$

Bài 23 trang 79 SBT Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Vì sao?

a) Nếu độ dài trung đoạn của một hình chóp tứ giác đều tăng lên $n$ lần $\left(n>1\right)$ và độ dài cạnh đáy không đổi thì diện tích xung quanh của hình chóp tứ giác đều đó cũng tăng lên $n$ lần.

b) Nếu độ dài cạnh đáy của một hình chóp tứ giác đều tăng lên $n$ lần $\left(n>1\right)$ và chiều cao không đổi thì thể tích của hình chóp tứ giác đều đó cũng tăng lên $n$ lần.

Lời giải:

Gọi độ dài cạnh đáy, độ dài trung đoạn, chiều cao ban đầu của một hình chóp tứ giác đều lần lượt là $a,d,h$ (cùng đơn vị đo, $a>0,d>0,h>0$).

a)     Diện tích xung quanh của hình chóp tứ giác đều ban đầu là: $\frac{1}{2}.4a.d=2ad$

Diện tích xung quanh của hình chóp tứ giác đều mới là: $\frac{1}{2}.4a.nd=n.2ad$

Do đó, diện tích xung quanh của hình chóp tứ giác đều mới gấp $n$ lần diện tích xung quanh của hình chóp tứ giác đều ban đầu.

Vậy phát biểu a là đúng.

b)    Thể tích của hình chóp tứ giác đều ban đầu là:

$\frac{1}{3}.a.a.h=\frac{1}{3}.a^2.h$

Thể tích của hình chóp tứ giác đều mới là:

$\frac{1}{3}.na.na.h=n^2.\frac{1}{3}{a}^{2}h$

Do đó, thể tích của hình chóp tứ giác đều mới gấp $n^2$ lần thể tích của hình chóp tứ giác đều ban đầu.

Vậy phát biểu b là sai.

Bài 24 trang 79 SBT Toán 8 Tập 1: Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng chiều cao. Chứng minh thể tích của hình chóp tứ giác đều đó bằng một phần ba thể tích của hình lập phương có độ dài cạnh bằng độ dài cạnh đáy của hình chóp tứ giác đều đó.

Lời giải:

Gọi độ dài cạnh đáy và chiều cao của hình chóp tứ giác đều là $a\left(a>0\right)$.

Do hình lập phương có độ dài cạnh bằng độ dài cạnh đáy của hình chóp tứ giác đều nên độ dài cạnh của hình lập phương là $a$.

Thể tích của hình chóp tứ giác đều là: $\frac{1}{3}.a^2.a=\frac{1}{3}.a^3$

Thể tích của hình lập phương là $a^3$

Vậy thể tích của hình chóp tứ giác đều bằng một phần ba thể tích của hình lập phương.

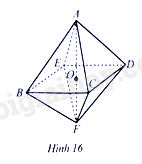
Bài 25 trang 79 SBT Toán 8 Tập 1: Cho hai hình chóp đều $A.BCDE$ và $F.BCDE$ lần lượt có chiều cao là $AO$ và $FO$ (Hình 16). Tính tỉ số thể tích của hình chóp tứ giác đều $A.BCDE$ và $F.BCDE$ biết $FO=k.AO\left(k>0\right)$.

Lời giải:

Thể tích của hình chóp tứ giác đều $A.BCDE$ là: $\frac{1}{3}.B{C}^2.AO$

Thể tích của hình chóp tứ giác đều $F.BCDE$ là:

$\frac{1}{3}.B{C}^2.FO=\frac{1}{3}.B{C}^2.k.AO=k.\frac{1}{3}.B{C}^2.AO$

Vậy tỉ số thể tích của hình chóp tứ giác đều $A.BCDE$ và $F.BCDE$ là $\frac{1}{k}$.

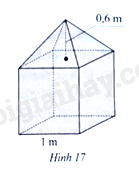
Bài 26 trang 79 SBT Toán 8 Tập 1: Hình 17 mô tả một khối bê tông mác 200 dùng trong việc xây cầu. Khối bê tông đó gồm hai phần: phần dưới có dạng hình lập phương với độ dài cạnh bằng 1 m, phần trên có dạng hình chóp tứ giác đều với chiều cao bằng 0,6 m. Cần phải chuẩn bị bao nhiêu tấn xi măng và bao nhiêu mét khối nước để làm khối bê tông đó? Biết rằng 1 m³ bê tông mác 200 cần khoảng 350,55 kg xi măng và 185 lít nước.

Lời giải:

Thể tích của phần dưới khối bê tông là: $1^3=1\left(m^3\right)$

Thể tích của phần trên khối bê tông là: $\frac{1}{3}{.1}^2.0,6=0,2\left(m^3\right)$

Thể tích của khối bê tông là: $1+0,2=1,2\left(m^3\right)$

Đổi 350,55 kg = 0,35055 tấn; 185 lít = 0,185 $m^3$

Khối lượng xi măng cần dùng để làm khối bê tông đó là:

$1,2.0,35055=0,42066$ (tấn)

Lượng nước cần dùng để làm khối bê tông đó là:

$1,2.0,185=0,222\left(m^3\right)$.