Với giải sách bài tập Toán 11 Bài 31: Định nghĩa và ý nghĩa của đạo hàm sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán lớp 11 Bài 31: Định nghĩa và ý nghĩa của đạo hàm

Giải SBT Toán 11 trang 57

Bài 9.1 trang 57 SBT Toán 11 Tập 2: Tính (bằng định nghĩa) đạo hàm của hàm số y = 2x² + 3x – 1 tại điểm x₀ = 1.

Lời giải:

Tại điểm x₀ = 1 ta có y₀ = 2×1² + 3×1 – 1 = 4.

Với x ≠ 1, ta có $\frac{y-4}{x-1}=\frac{2x^2+3x-1-4}{x-1}$$=\frac{2x^2+3x-5}{x-1}$

$=\frac{\left(2x+5\right)\left(x-1\right)}{x-1}=2x+5$ .

Do đó y'(1) = $\underset{x\to 1}{\lim }\frac{y-4}{x-1}=$$\underset{x\to 1}{\lim }$(2x+5) = 7. Vậy y'(1) = 7.

Bài 9.2 trang 57 SBT Toán 11 Tập 2: Cho hàm số f(x) = x(2x – 1)². Tính f'(0) và f'(1).

Lời giải:

+ Có f'(0) = $\underset{x\to 0}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}$$=\underset{x\to 0}{\lim }\frac{x{\left(2x-1\right)}^2}{x}$$=\underset{x\to 0}{\lim }$(2x-1)² = 1.

Vậy f'(0) = 1.

+ Có f'(1) = $\underset{x\to 1}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}$$=\underset{x\to 1}{\lim }\frac{x{\left(2x-1\right)}^2-1}{x-1}$

$=\underset{x\to 1}{\lim }\frac{\left(x-1\right){\left(2x-1\right)}^2+{\left(2x-1\right)}^2-1}{x-1}$

$=\underset{x\to 1}{\lim }\frac{\left(x-1\right){\left(2x-1\right)}^2+\left(2x-1-1\right)\left(2x-1+1\right)}{x-1}$

$=\underset{x\to 1}{\lim }\frac{\left(x-1\right){\left(2x-1\right)}^2+4x\left(x-1\right)}{x-1}$

Vậy f'(1) = 5.

Bài 9.3 trang 57 SBT Toán 11 Tập 2: Cho hàm số f(x) = 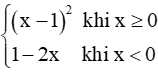. Tính f'(0).

Lời giải:

Ta có f(0) = (0 – 1)² = 1.

Ta có $\underset{x\to 0^{+}}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}$$=\underset{x\to 0^{+}}{\lim }\frac{{\left(x-1\right)}^2-1}{x}$$=\underset{x\to 0^{+}}{\lim }\frac{x^2-2x}{x}$$=\underset{x\to 0^{+}}{\lim }$(x-2) = -2 ;

$\underset{x\to 0^{-}}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}$$=\underset{x\to 0^{-}}{\lim }\frac{1-2x-1}{x}$$=\underset{x\to 0^{-}}{\lim }\frac{-2x}{x}=-2$.

Suy ra $\underset{x\to 0}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}=\underset{x\to 0^{+}}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}=\underset{x\to 0^{-}}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}=-2$ .

Vậy f'(0) = −2.

Bài 9.4 trang 57 SBT Toán 11 Tập 2: Tính đạo hàm của hàm số:

a) y = ax² (a là hằng số) tại điểm x₀ bất kì.

b) $y=\frac{1}{x-1}$ tại điểm x₀ bất kì, x₀ ≠ 1.

Lời giải:

a) Đặt y = f(x) = ax².

Ta có y'(x₀) = $\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{a{x}^2-a{x}_0^2}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{a\left(x^2-x_0^2\right)}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{a\left(x-x_0\right)\left(x+x_0\right)}{x-x_0}$

Vậy y'(x₀) = 2ax₀.

b) Đặt y = f(x) = $\frac{1}{x-1}$.

Ta có y'(x₀) = $\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{\frac{1}{x-1}-\frac{1}{x_0-1}}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{\frac{x_0-1-\left(x-1\right)}{\left(x-1\right)\left(x_0-1\right)}}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{\frac{\left(x_0-x\right)}{\left(x-1\right)\left(x_0-1\right)}}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{-1}{\left(x-1\right)\left(x_0-1\right)}$$=\frac{-1}{{\left(x_0-1\right)}^2}$.

Vậy $y^{\text{'}}\left(x_0\right)=\frac{-1}{{\left(x_0-1\right)}^2}$ , x₀ ≠ 1.

Bài 9.5 trang 57 SBT Toán 11 Tập 2: Tìm tọa độ điểm M trên đồ thị hàm số y = x³ + 1, biết hệ số góc của tiếp tuyến của đồ thị hàm số tại M bằng 3.

Lời giải:

Giả sử M(a; a³ + 1) là điểm thuộc đồ thị hàm số y = x³ + 1.

Đặt y = f(x) = x³ + 1. Có y'(a) = $\underset{x\to a}{\lim }\frac{f\left(x\right)-f\left(a\right)}{x-a}$

$=\underset{x\to a}{\lim }\frac{x^3+1-\left(a^3+1\right)}{x-a}$$=\underset{x\to a}{\lim }\frac{x^3-a^3}{x-a}$

$=\underset{x\to a}{\lim }\frac{\left(x-a\right)\left(x^2+ax+a^2\right)}{x-a}$

$=\underset{x\to a}{\lim }\left(x^2+ax+a^2\right)=3a^2$.

Theo đề bài, ta có y'(a) = 3 nên 3a² = 3 $\iff$ a = 1 hoặc a = −1.

Với a = 1 thì M(1; 2);

Với a = −1 thì M(−1; 0).

Vậy M(1; 2) và M(−1; 0) là tọa độ điểm cần tìm.

Bài 9.6 trang 57 SBT Toán 11 Tập 2: Viết phương trình tiếp tuyến của đồ thị hàm số y = −3x², biết tiếp tuyến đó song song với đường thẳng có phương trình y = 6x + 5.

Lời giải:

Đặt y = f(x) = −3x². Với x₀ bất kì, ta có:

y'(x₀) = $\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{-3x^2+3x_0^2}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{-3\left(x^2-x_0^2\right)}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{-3\left(x-x_0\right)\left(x+x_0\right)}{x-x_0}$

Khi đó hệ số góc của tiếp tuyến có dạng k = y'(x₀) = −6x₀ (x = x₀ là hoành độ tiếp điểm).

Do tiếp tuyến song song với đường thẳng có phương trình y = 6x + 5 nên hệ số góc của tiếp tuyến là k = 6. Do đó −6x₀ = 6 $\iff$ x₀ = −1.

Với x₀ = −1 thì y(−1) = −3.

Khi đó, ta có phương trình tiếp tuyến là: y + 3 = 6(x + 1) hay y = 6x + 3.

Vậy y = 6x + 3 là phương trình tiếp tuyến cần tìm.

Bài 9.7 trang 57 SBT Toán 11 Tập 2: Vị trí của một vật chuyển động thẳng được cho bởi phương trình s = t³ – 4t² + 4t, trong đó t tính bằng giây và s tính bằng mét. Tính vận tốc của vật tại các thời điểm t = 3 giây và t = 5 giây.

Lời giải:

Ta có vận tốc của vật tại thời điểm t₀ bất kì là

v(t₀) = s'(t₀) = $\underset{t\to t_0}{\lim }\frac{s\left(t\right)-s\left(t_0\right)}{t-t_0}$

$=\underset{t\to t_0}{\lim }\frac{t^3-4t^2+4t-\left(t_0^3-4t_0^2+4t_0\right)}{t-t_0}$

$=\underset{t\to t_0}{\lim }\frac{\left(t^3-t_0^3\right)-4\left(t^2-t_0^2\right)+4\left(t-t_0\right)}{t-t_0}$

$=\underset{t\to t_0}{\lim }\frac{\left(t-t_0\right)\left(t^2+t{t}_0+t_0^2\right)-4\left(t-t_0\right)\left(t+t_0\right)+4\left(t-t_0\right)}{t-t_0}$

Vận tốc của vật tại thời điểm t = 3 giây là v(3) = 3×3² − 8×3 + 4 = 7 m/s.

Vận tốc của vật tại thời điểm t = 5 giây là v(5) = 3×5² − 8×5 + 4 = 39 m/s.

Xem thêm các bài giải SBT Toán 11 Kết nối tri thức hay, chi tiết khác: