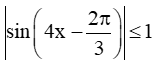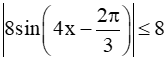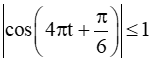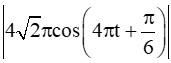Với giải sách bài tập Toán 11 Bài 32: Các quy tắc tính đạo hàm sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán lớp 11 Bài 32: Các quy tắc tính đạo hàm
Bài 9.8 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) y = (x + 1)2(x2 – 1);
b) .
Lời giải:
a) Ta có: y' = ((x + 1)2)'(x2 – 1) + (x + 1)2(x2 – 1)'
= 2(x + 1)(x2 – 1) + 2x(x + 1)2
= 2x3 – 2x + 2x2 – 2 + 2x3 + 4x2 + 2x = 4x3 + 6x2 – 2.
Vậy y' = 4x3 + 6x2 – 2.
b)
.
Bài 9.9 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) ;
b) .
Lời giải:
a)
.
Vậy .
b)
.
Bài 9.10 trang 60 SBT Toán 11 Tập 2: Cho hàm số và . Tính f'(0) – g'(1).
Lời giải:
Có
.
Khi đó .
Có .
Khi đó .
Do đó f'(0) – g'(1) = . Vậy f'(0) – g'(1) = 0.
Bài 9.11 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của hàm số .
Lời giải:
Có
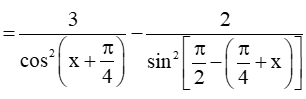
Bài 9.12 trang 60 SBT Toán 11 Tập 2: Cho hàm số . Tính đạo hàm f'(x) và chứng tỏ f'(x) = 0 với mọi x ℝ.
Lời giải:
Có
= -sin2x + 2cossin2x = -sin2x + sin2x = 0.
Vậy f'(x) = 0 với mọi x ℝ.
Bài 9.13 trang 60 SBT Toán 11 Tập 2: Cho hàm số f(x) = 4sin2. Chứng minh rằng |f'(x)| ≤ 8 với mọi x ℝ. Tìm x để f'(x) = 8.
Lời giải:
+ Có 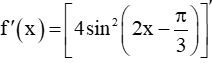
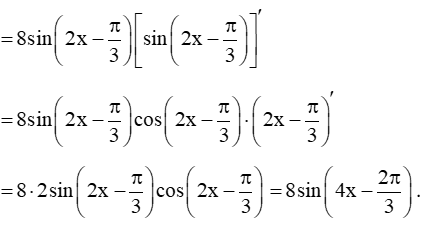
Vì 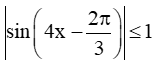 với mọi x ℝ nên
với mọi x ℝ nên 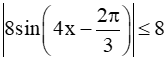 với mọi x ℝ .
với mọi x ℝ .
Vậy |f'(x)| ≤ 8 với mọi x ℝ.
+ Có f'(x) = 8 8sin=8
(k ℤ)
(k ℤ)
(k ℤ).
Vậy f'(x) = 8 khi với k ℤ.
Bài 9.14 trang 60 SBT Toán 11 Tập 2: Biết y là hàm số của x thỏa mãn phương trình xy = 1 + lny. Tính y'(0).
Lời giải:
Đạo hàm hai vế của phương trình đã cho, ta có
(xy)' = (1 + lny)' y + xy' =
y = - xy' y = y'.
y = y' y' = .
Tại x = 0 thay vào phương trình xy = 1 + lny ta được lny = −1 y = e−1.
Do đó .
Vậy .
Bài 9.15 trang 60 SBT Toán 11 Tập 2: Một vật được phóng thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là v0 (m/s) (bỏ qua sức cản của không khí) thì độ cao h của vật (tính bằng mét) sau t giây được cho bởi công thức (g là gia tốc trọng trường). Tính vận tốc khi vật chạm đất.
Lời giải:
Vận tốc của vật tại thời điểm t là v(t) = h'(t) = = vo - gt.
Tại thời điểm vật chạm đất thì h = 0 (t > 0) tức là vot - gt2 = 0
.
Vận tốc khi vật chạm đất là (m/s).
Vậy vận tốc khi vật chạm đất là −v0 m/s.
Bài 9.16 trang 60 SBT Toán 11 Tập 2: Chuyển động của một hạt trên một dây rung được cho bởi công thức , trong đó s tính bằng centimét và t tính bằng giây. Tính vận tốc của hạt sau t giây. Vận tốc cực đại của hạt là bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
Lời giải:
Vận tốc của hạt sau t giây là v(t) = s'(t) =
.
Vì 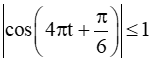 nên
nên 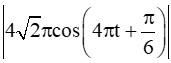 4 hay |v(t)|4.
4 hay |v(t)|4.
Do đó vận tốc cực đại của hạt là 417,8 m/s đạt được khi 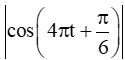 = 1
= 1
, với k ℕ*.
Vậy vận tốc cực đại của hạt khoảng 17,8 m/s khi ,với k ℕ*.
Xem thêm các bài giải SBT Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 31: Định nghĩa và ý nghĩa của đạo hàm
Bài 32: Các quy tắc tính đạo hàm
Bài 33: Đạo hàm cấp hai
Bài tập ôn tập cuối năm
Lý thuyết Các quy tắc tính đạo hàm
1. Đạo hàm của tổng, hiệu, tích, thương
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng (a; b). Khi đó
(k là hằng số);
.
2. Đạo hàm của hàm hợp
Nếu hàm số u = g(x) có đạo hàm tại x là và hàm số y = f(u) có đạo hàm tại u là thì hàm hợp y = f(g(x)) có đạo hàm tại x là .
3. Bảng đạo hàm của một số hàm số sơ cấp cơ bản và hàm hợp