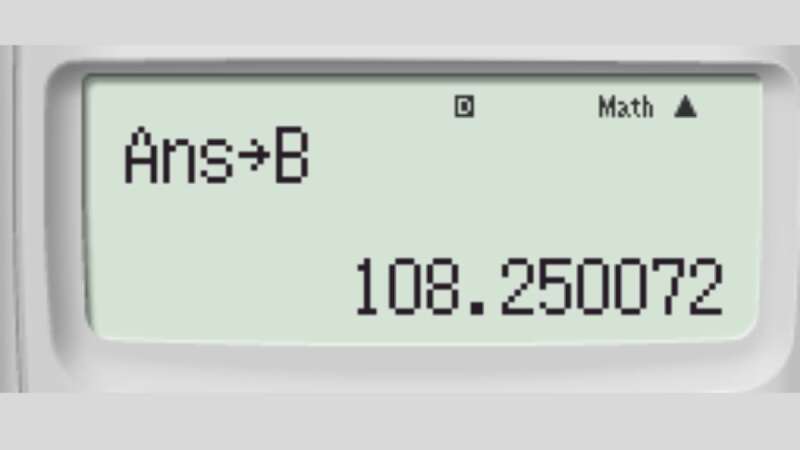
Tailieumoi.vn xin giới thiệu Cách bấm đạo hàm trên máy tính cầm tay Casio chi tiết, dễ hiểu được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết hướng dẫn cách bấm đạo hàm trên máy tính cầm tay Casio chi tiết, dễ hiểu. Ngoài ra bài viết còn gồm các bài tập liên quan đến bấm đạo hàm trên máy tính Casio:

Cách bấm đạo hàm trên máy tính cầm tay Casio chi tiết, dễ hiểu

1. Đạo hàm là gì?

- Trong giải tích toán học, đạp hàm là một hàm mô tả sự biến thiên tại một điểm. Nói cách khác, đạo hàm là tỷ số giữa số gia và hàm số tại một điểm x0. Độ lớn của biến thể và hướng của biến thể đại diện cho giá trị của đạo hàm. Tuy nhiên, theo một định nghĩa khác của Wikipedia thì đạo hàm được hiểu là sự biến thiên lên xuống của hàm số tại điểm thay đổi. Ngoài ra tròn Vật lý đạo hàm được coi là vận tốc tức thời khi một vật đang chuyển động.

Đạo hàm của hàm y = f(x) được ký hiệu là y'(x0) hoặc f'(x0)

hoặc 

• Số gia của đối số là: 
• Số gia của hàm là: 

- Ý nghĩa của đạo hàm được thể hiện qua hai khía cạnh, một là khía cạnh hình học trong Toán học, hai là khía cạnh Vật lý.

- Về mặt hình học cụ thể trong môn Toán lớp 11, đạo hàm có các ý nghĩa sau: Cho hàm số y = f(x) xác định trên khoảng (a;b) và có đạo hàm tại , gọi (C) là đồ thị của hàm số đó.

+ Định lí 1: Đạo hàm  của hàm số f(x) tại điểm xo là hệ số góc của tiếp tuyến MoT của (C) tại điểm M0 (x0;f (x0))

+ Định lí 2: Phương trình tiếp tuyến của đồ thị (C) của hàm số y = f(x) tại điểm M0 (x0; f (x0)) là: y-y0=f'(x)(x-x0)

- Về mặt vật lý, đạo hàm thứ 11 được coi là vận tốc tức thời khi một vật đang chuyển động, Cụ thể, chúng tôi xem xét chuyển động tuyến tính được xác định bởi phương trình: s=f(t), trong đó f(t) là một hàm có đạo hàm. Khi đó, vận tốc tức thời xác định tại thơi điểm t0  là đạo hàm của hàm s=f(t) tại t0.

2. Cách tính đạo hàm bằng máy tính Casio Fx - 580

2.1. Tổng quan các bước tiến hành

Để thực hiện cách bấm máy tính đạo hàm nhanh và có kết quả chính xác nhất, bạn cần phải trang bị cho mình các kiến thức nền tảng liên quan đến máy tính Casio. Sau đây, công thức cần nhớ khi thực hiện bấm máy:

- Lệnh bấm tính đạo hàm cấp 1: Nhấn 

Quy trình bấm đạo hàm cấp 1: 

+ Bước 1: Nhấn

+ Bước 2: Nhập biểu thức  và nhấn phím 

- Tính đạo hàm cấp 2: 

Quy trình bấm đạo hàm cấp 2:

+ Bước 1: Tính đạo hàm  tại điểm x=x0

+ Bước 2: Tính đạo hàm cấp 1 tại điểm x=x0+ 0,000001

+ Bước 3: Nhập vào máy tính       và nhấn phím

* Ví dụ minh họa: tính dạo hàm cấp 1:

Cho hàm số sau:  . Hãy tính đạo hàm của hàm số tại x=3. Hướng dẫn bấm máy như sau:

Bước 1: Nhấn tổ hợp phím   ta được 

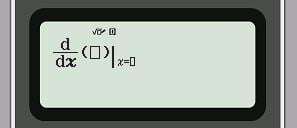
Bước 2: Nhập hàm số và x=3, ta được: 

Bước 3: nhấn phím  có kết quả sau: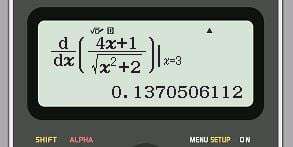 

Vậy kết quả đạo hàm của hàm số là: 0,1370506112

2.2. Các ví dụ minh họa

* Ví dụ đạo hàm cấp 2:

Hãy tính đạo hàm cấp 2 của hàm số sau:

Tính f''(2) biết . Sau đây là cách bấm máy tính đạo hàm cấp 2: 

Bước 1: gán 10-9 vào biến nhớ A =

Bước 2: Tính f'(A+2) gán vào biến nhớ B

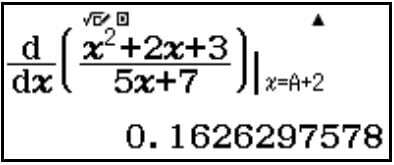
Bước 3: Tính f' (2) gán vào biến nhớ 

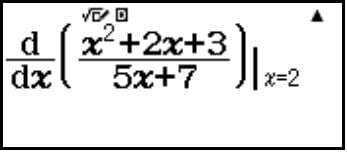
Bước 4: Tính . Kết quả của phép tính này là đạo hàm cấp 2 của hàm số.

3. Cách tính đạo hàm cấp 2 trên máy Casio 880  BTG

3.1.  Tổng quan các bước tiến hành 

Ví dụ 1: Tính đạo hàm cấp hai của hàm số f(X)= tại các điểm -1; 0; 1.

 - Bước 1: Gán hàm số  vào hàm nhớ f(x)

+ Bước 1.1. Nhấn phím FUNCTION => chọn Define f(x)=> nhấn phím OK

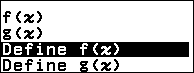
+Bước 1.2.  Nhập hàm số  => nhấm phím EXE

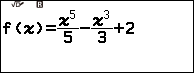
- Bước 2: Mở bảng tính Spreadsheet

Nhấn phím HOME => cHỌN Spreadsheet => nhấm phím OK

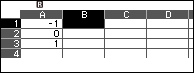
- Bước 3: Nhập -1, 0, 1 vào các ô A1, A2, A3

Nhập -1 => nhấn phím EXE => nhập 0=> nhấn phím EXE => nhập 1 => nhấn phím EXE

- Bước 4: Chọn ô B1 rồi sử dụng tính năng Fill Formula với Form là (d/dx(f(x), A1+10^(-9)) - d/dx)(f(x),A1))  10^(-9) và Rang là B1:B3

+ Bước 4.1. Chọn ô B1

+ Bước 4.2. Nhấn phím TOOLS => chọn Fill Formula => nhấn phím OK

+ Bước 4.3. Nhập (d/dx(f(x),A1+10^(-9))-s/dx(f(x),A1))  10^(-9)=> Nhấn phím EXE => nhập B1:B3 => nhấn phím EXE => nhấn phím 

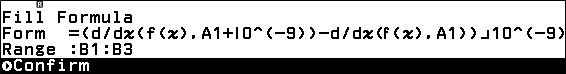
Bước 5: Quan sát cột B

Những giá trị ở cột B chính là gái trị gần đúng của đạo hàm cấp 2 của hàm số f(x) tại các điểm ở cột A

Vậy đạo hàm cấp 2 của hàm số đã cho tại các điểm -1, 0, 1 lần lượt là -2, 0, 2.

3.2. Cách tính đạo hàm cấp 2 tại nhiều điểm:

Có hai tính năng giúp chúng tra tính nhanh đạo hàm cấp 2 tại nhiều điểm là tính năng bảng tính Spreadsheet và tính năng bảng giá trị Table trên máy tính Casio

Cách 1. Sử dụng tính năng bảng tính Spreadsheet

Bước 1. Gán hàm số cần tính đạo hàm cấp 2 vào hàm nhớ f(x)

Bước 2. Mở bảng tính Spreadsheet

Bước 3: Nhập các điểm cần tính đạo hàm  cấp hai vào các ô A1, A2, A3..

Bước 4. Chọn ô B1 rồi sử dụng tính  năng Fill Formula với Form là (d/dx(f(x),A1+10^(-9))-d/dx(f(x),A1)) 10^(-9) và Rang là B1:Bn

Chú ý: n là bao nhiêu phụ thuộc vào số lượng điểm cần tính các bạn nhé.

Bước 5. Quan sát cột B: Những giá trị ở cột B chính là giá trị gần đúng của đạo hàm cấp 2 của hàm số f(x) tại các điểm ở cột A.

Cách 2. Sử dụng tính năng bảng giá trị Table

Bước 1. Mở tính năng tạo bảng giá trị Table

Bước 2. Nhập f(X) là 

Bước 3. Giữ nguyên các giá trị Start =1, End=5, Step=1

Bước 4. Nhập các giá trị cần tính đạo hàm cấp hai vào cột x

* Những lưu ý khi bấm đạo hàm trên máy tính Casio 880

- Khi sử dụng hàm lương giác f(x), hãy chỉ định Radian làm Angle Unit trên menu SETTINGS

- Giá trị tol nhỏ hơn cho độ chính xác cao hơn nhưng cũng làm mất nhiều thời gian tính toán. Khi chỉ định tol, hãy sử dụng giá trị từ 1 x 10-22 trở lên.

- Kết quả có thể không chính xác hoặc bị cáo lỗi nếu:

+ Các điểm không kế tiếp trong các giá trị x

+ Sự thay đổi đột ngột trong các giá trị x

+ Bao hàm điểm cực đại và điểm cực tiểu trong các giá trị x

+ Bao hàm điểm uốn trong các giá trị x

+ Bao hàm các điểm không vi phân được trong giá trị x

+ Kết quả phép tính vi phân gần bằng 0

+ Tính năng Derivative(d/dx) không khả dụng trng các ứng dụng số phức Complex, hệ cơ số Base-N và hộp toán học Math Box.

4. Cách tính đạo hàm bằng máy tính Vinacal

Bước 1: Nhập vào máy tính

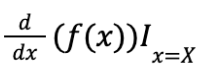
Bước 2: CALC X = 100 sau đó ta tiến hành biểu diễn số đó qua X và thế là xong.

5. Cách tính đạo hàm logarit bằng máy tính

5.1. Tổng quan các bước tiến hành

Tính đạo hàm logarit bằng máy tính là kỹ năng cần thiết áp dụng hiệu quả trong đề thi THPT quốc gia. Khi tiến hành thực hiện, các e cần nắm vững 3 bước sau đây: Cho hàm số y=f(x). Tính đạo hàm logarit bằng máy tính:

Bước 1: Chọn x=x0 bất kì thuộc tập xác định

Bước 2: Tính đạo hàm của hàm số y=f(x) tại x=x0 và ghi lại kết quả.

Bước 3: Thay x=x0 vào các đáp án A, B, C và D và so sánh với kết quả vừa tính được ở bước 2.

5.2. Ví dụ minh họa 

Câu hỏi:  Đạo hàm của hàm số f(x)=log₂(2x²+1) là 

A.

B.

C. 

D. 

Giải: 

Bước 1: Chọn x = 2 thuộc tập xác định của hàm số f(x) thay vào biểu thức sau:

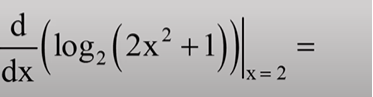
Bước 2: Tính đạo hàm của hàm số f(x) trên tại x = 2. Bấm máy tính ta ra được kết quả:

Bước 3: Thay giá trị x = 2 vào từng đáp án A, B, C và D và so sánh với kết quả vừa tính được ở bước 2:

- Thay x=2 vào đáp án A: 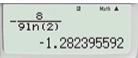 => Loại

- Thay x=2 vào đáp án B: 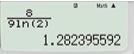=> Chọn

Ta làm tương tự với 3 đáp án còn lại nếu chưa chắc chắn. Sau khi thay, ta ra được kết quả đúng là đáp án B.

6. Một số thủ thuật tính đạo hàm bằng máy tính 

Ví dụ tính đạo hàm cấp 1

Cho hàm số

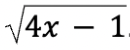
Tính đạo hàm của hàm số tại x = 2

Bước 1: Bấm tổ bàn phím Shift + nút đạo hàm, ta được:

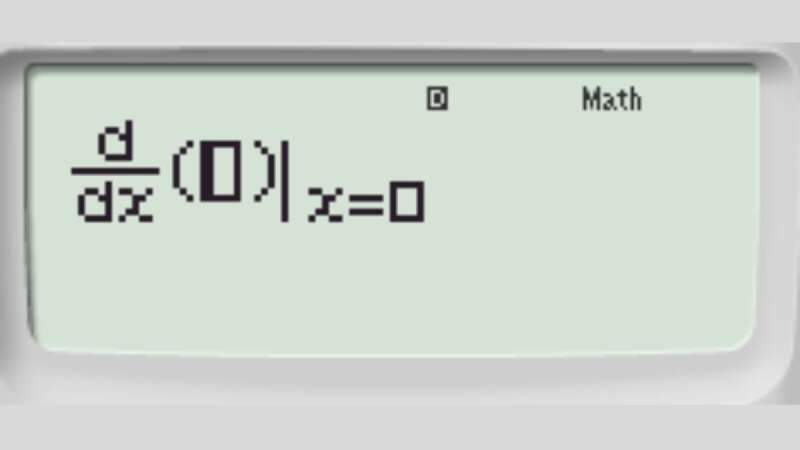
Bước 2: Nhập hàm số y = \sqrt {4x - 1} và x = 2 ta được

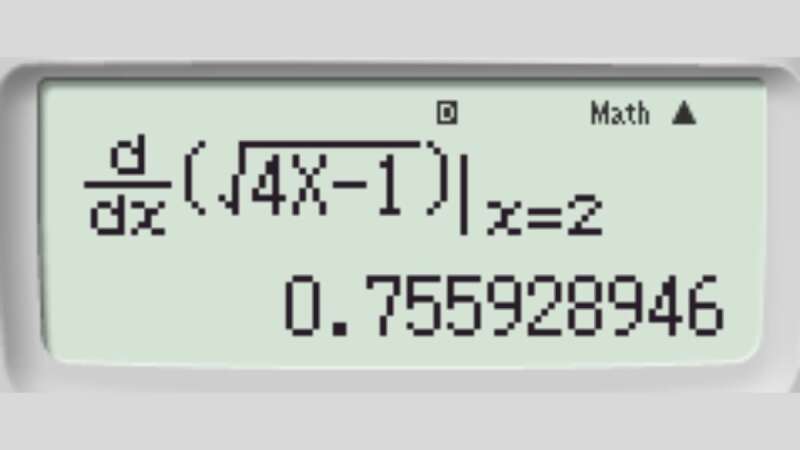
Nhấn “=” ta được kết quả cần tìm:

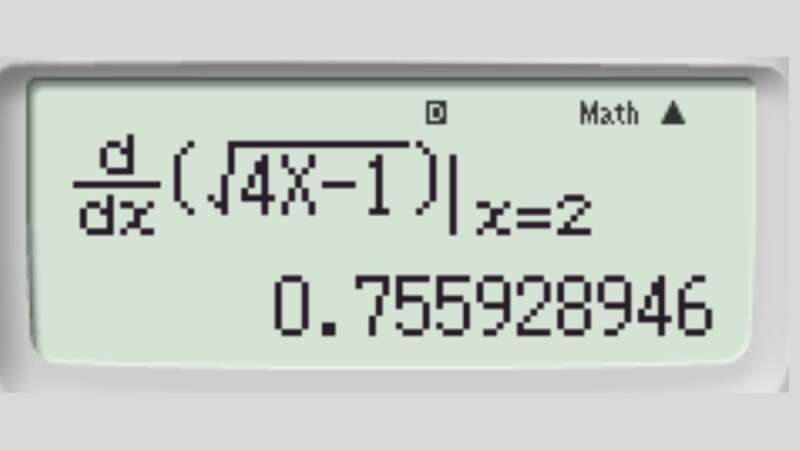
Ví dụ tính đạo hàm cấp 2

Ví dụ 2: Tính giá trị gần đúng đạo hàm cấp hai của hàm số

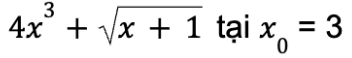
tại x0 = 3

Bước 1: Tính đạo hàm cấp 1 của hàm số tại tại x0 = 3

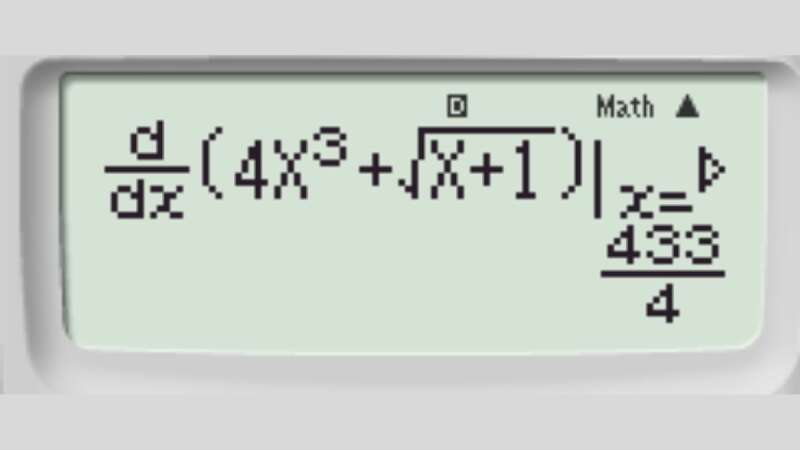
Bước 2: Lưu kết quả vừa tìm được vào hàm A Bấm tổ hợp phím Shift + RLC + (-) ta có được:

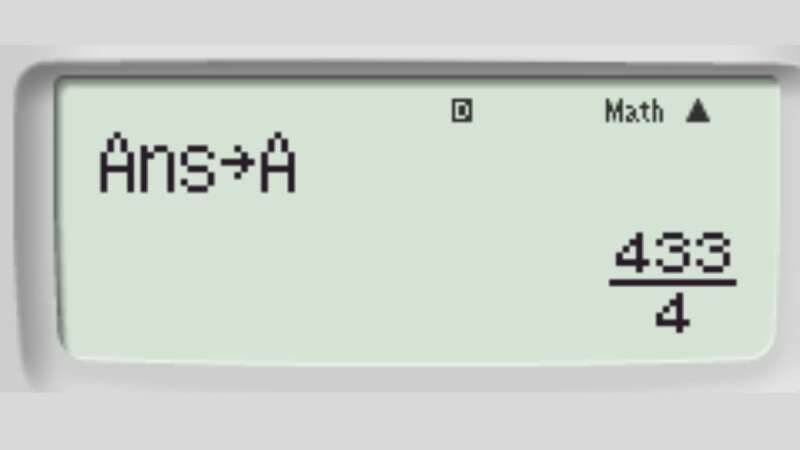
Bước 3: Tính đạo hàm cấp 1 của hàm số tại tại x0 = 3 + 0.000001

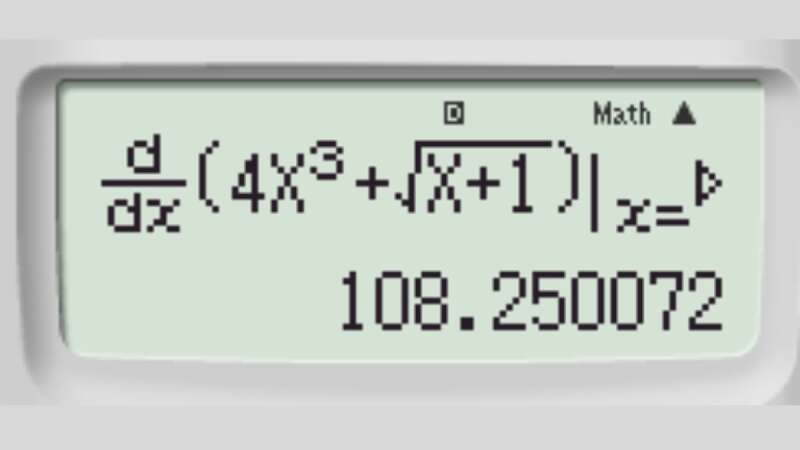
Bấm tổ hợp phím Shift + RLC + ‘’’ ta có được