Với lời giải Toán 11 trang 33 Tập 2 chi tiết trong Bài 4: Phương trình, bất phương trình mũ và lôgarit sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 Bài 4: Phương trình, bất phương trình mũ và lôgarit

Bài 2 trang 33 Toán 11 Tập 2: Giải các phương trình sau. Làm tròn kết quả đến hàng nghìn.

a) 3^{x + 2} = 7;

b) 3 . 10^{2x + 1} = 5.

Lời giải:

a) 3^{x + 2} = 7 ⇔ x + 3 = log₃ 7

⇔ x = –3 + log₃ 7 ⇔ x ≈ –0,229.

Vậy nghiệm của phương trình đã cho là x ≈ –0,229.

b) $3.{10}^{2x+1}=5\iff {10}^{2x+1}=\frac{5}{3}\iff 2x+1=\log \frac{5}{3}$

$\iff 2x=\log \frac{5}{3}-1\iff x=\frac{1}{2}\left(\log \frac{5}{3}-1\right)\iff x\approx -\mathrm{0,389}$.

Vậy nghiệm của phương trình đã cho là x ≈ –0,389.

Bài 3 trang 33 Toán 11 Tập 2: Giải các phương trình sau:

a) log₆ (4x + 4) = 2;

b) log₃ x – log₃ (x – 2) = 1.

Lời giải:

a) Điều kiện: 4x + 4 > 0 ⇔ x > –1

Khi đó: log₆ (4x + 4) = 2 ⇔ 4x + 4 = 6²

⇔ 4x + 4 = 36 ⇔ 4x = 32 ⇔ x = 8 (TMĐK)

Vậy nghiệm của phương trình đã cho là x = 8.

b) Điều kiện: .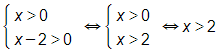

Khi đó: log₃ x – log₃ (x – 2) = 1

⇔ log₃ x – log₃ (x – 2) = 1

⇔ log₃ x = log₃ (x – 2) + 1

⇔ log₃ x = log₃ (x – 2) + log₃ 3

⇔ log₃ x = log₃ 3(x – 2)

⇔ x = 3(x – 2) ⇔ 2x = 6 ⇔ x = 3 (TMĐK)

Vậy nghiệm của phương trình đã cho là x = 3.

Bài 4 trang 33 Toán 11 Tập 2: Giải các bất phương trình sau:

a)${\left(\frac{1}{3}\right)}^{2x+1}\le 9$;

b) 4^x > 4^{x – 2}.

Lời giải:

a)${\left(\frac{1}{3}\right)}^{2x+1}\le 9\iff {\left(\frac{1}{3}\right)}^{2x+1}\le {\left(\frac{1}{3}\right)}^{-2}$

$\iff 2x+1\le -2$(do $0<\frac{1}{3}<1$)

$\iff 2x>-3\iff x>-\frac{3}{2}$.

Vậy nghiệm của bất phương trình là $x>-\frac{3}{2}$.

b)$4^x>4^{x-2}\iff {\left(2^2\right)}^x>4^{x-2}\iff 2^{2x}>4^{x-2}$

$\iff 2x>x-2$ (do 2 > 1)

⇔ x > – 2.

Vậy nghiệm của bất phương trình là x > – 2.

Bài 5 trang 33 Toán 11 Tập 2: Giải các bất phương trình sau:

a)log₂ (x – 2) < 2;

b)log (x + 1) ≥ log (2x – 1).

Lời giải:

a) Điều kiện: x – 2 > 0 ⇔ x > 2

Khi đó: log₂ (x – 2) < 2⇔ x – 2 < 2²

⇔ x – 2 < 4 ⇔ x < 6.

Kết hợp với điều kiện ta được nghiệm của bất phương trình là 2 < x < 6.

b)Điều kiện:

Khi đó: log (x + 1) ≥ log (2x – 1)

⇔x + 1 ≥ 2x – 1 ⇔x ≥ –2⇔x ≤ 2.

Kết hợp với điều kiện ta được nghiệm của bất phương trình là $\frac{1}{2}<x\le 2$.

Bài 6 trang 33 Toán 11 Tập 2: Chất phóng xạ polonium-210 có chu kì bán rã là 138 ngày. Điều này có nghĩa là cứ sau 138 ngày, lượng polonium còn lại trong một mẫu chỉ bằng một nửa lượng ban đầu. Một mẫu 100g có khối lượng polonium-210 còn lại sau t ngày được tính theo công thức $M\left(t\right)=100{\left(\frac{1}{2}\right)}^{\frac{t}{138}}\left(g\right)$.

(nguồn://pubchem.ncbi.nlm.nih.gov/element/Polonium#section=

Atiomc-Mass-Half-Life-anh-Decay)

a) Khối lượng polonium-210 còn lại bao nhiêu sau 2 năm?

b) Sau bao lâu thì còn lại 40 g polonium-210.

Lời giải:

a) Sau 2 năm (tức t = 730), khối lượng polonium-210 còn lại là:

$M\left(730\right)=100{\left(\frac{1}{2}\right)}^{\frac{730}{138}}\approx \mathrm{1,92}\left(g\right)$.

Vậy khối lượng polonium-210 còn lại sau 2 năm khoảng 1,92 g.

b) Ta có $M\left(t\right)=40\iff 100{\left(\frac{1}{2}\right)}^{\frac{t}{138}}=40\iff {\left(\frac{1}{2}\right)}^{\frac{t}{138}}=\frac{2}{5}$

$\iff \frac{t}{138}={\log }_{\frac{1}{2}}\frac{2}{5}\iff t=138{\log }_{\frac{1}{2}}\frac{2}{5}\approx \mathrm{182,43.}$

Vậy sau khoảng 182,43 ngày thì còn lại 40 g polonium-210.

Bài 7 trang 33 Toán 11 Tập 2: Nhắc lại rằng, mức cường độ âm L được tính bằng công thức $L=\log \left(\frac{I}{I_0}\right)\left(dB\right)$, trong đó I là cường độ của âm tính bằng W/m2 và $I_0={10}^{12}\text{\hspace{0.17em}\hspace{0.17em}W}/m^2.$

(Nguồn: Vật lí 12, NXB Giáo dục Việt Nam, năm 2017, trang 52)

a) Một giáo viên đang giảng bài trong lớp học, có mức cường độ âm là 50 dB. Cường độ âm của giọng nói giáo viên bằng bao nhiêu?

b) Mức cường độ âm trong một nhà xưởng thay đổi trong khoảng từ 75 dB đến 90 dB. Cường độ âm trong nhà xưởng này thay đổi trong khoảng nào?

Lời giải:

a) Ta có $L=50\iff 10\log \left(\frac{I}{I_0}\right)=50\iff 10\log \left(\frac{I}{{10}^{-12}}\right)=50$

$\iff \log \left(\frac{I}{{10}^{-12}}\right)=5\iff \frac{I}{{10}^{-12}}={10}^5\iff I={10}^{-7}\left(W/m^2\right)$.

Vậy cường độ âm của giọng nói giáo viên bằng 10^–7 (W/m²).

b) Ta có $75\le L\le 90\iff 75\le 10\log \left(\frac{I}{I_0}\right)\le 90$

$\iff 75\le 10\log \left(\frac{I}{{10}^{-12}}\right)\le 90\iff \mathrm{7,5}\le \log \left(\frac{I}{{10}^{-12}}\right)\le 9$

$\iff {10}^{\mathrm{7,5}}\le \frac{I}{{10}^{-12}}\le {10}^9\iff {10}^{-\mathrm{4,5}}\le I\le {10}^{-3}\left(W/m^2\right)$.

Vậy cường độ âm trong nhà xưởng này thay đổi trong khoảng 10^–4,5 (W/m²) đến 10^–3 (W/m²).