Với giải sách bài tập Toán 11 Bài 2: Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 2: Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất
A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 2”;
B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 5”;
C: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 2 hoặc chia hết cho 5”;
D: “Số xuất hiện trên thẻ được rút ra là số vừa chia hết cho 2 vừa chia hết cho 5”.
a) Biến cố C là biến cố hợp của:
A. Biến cố B và biến cố D;
B. Biến cố A và biến cố D;
C. Biến cố A và biến cố B;
D. Biến cố A và biến cố D hoặc biến cố B và biến cố D.
b) Biến cố D là biến cố giao của:
A. Biến cố B và biến cố C;
B. Biến cố A và biến cố B;
C. Biến cố A và biến cố C;
D. Biến cố A và biến cố C hoặc biến cố B và biến cố C.
Lời giải:
a) Đáp án đúng là: C
Biến cố hợp của hai biến cố A và B là “Số xuất hiện trên thẻ được rút ra là số chia hết cho 2 hoặc chia hết cho 5”, hay biến cố C là biến cố hợp của biến cố A và biến cố B.
b) Đáp án đúng là: B
Biến cố giao của hai biến cố A và B là “Số xuất hiện trên thẻ được rút ra là số vừa chia hết cho 2 vừa chia hết cho 5”, hay biến cố D là biến cố giao của biến cố A và biến cố B.
a) Xét các biến cố sau:
A: “ Hai học sinh được chọn đều là học sinh nam”;
B: “ Hai học sinh được chọn đều là học sinh nữ”;
C: “ Hai học sinh được chọn có cùng giới tính”.
Trong ba biến cố A, B, C, biến cố nào là biến cố hợp của hai biến cố còn lại?
b) Xét các biến cố sau:
D: “Hai học sinh được chọn gồm một bạn nam và một bạn nữ”;
E: “Trong hai học sinh được chọn, có ít nhất một học sinh nữ”;
G: “Trong hai học sinh được chọn, có ít nhất một học sinh nam”.
Trong ba biến cố D, E, G biến cố nào là biến cố giao của hai biến cố còn lại?
Lời giải:
a) Biến cố hợp của hai biến cố A và B là “Hai học sinh được chọn có cùng giới tính”, hay biến cố C là biến cố hợp của biến cố A và biến cố B.
b) Biến cố giao của hai biến cố E và G là “Hai học sinh được chọn gồm một bạn nam và một bạn nữ”, hay biến cố D là biến cố giao của biến cố E và biến cố G.
M: “Trong 5 người được chọn, số nam lớn hơn 3”;
N: “Trong 5 người được chọn, số nữ nhỏ hơn 3”;
P: “Trong 5 người được chọn, số nam không vượt quá 3”.
Trong ba biến cố M, N, P, hai biến cố nào là xung khắc?
Lời giải:
Ta thấy, nếu biến cố M: “Trong 5 người được chọn, số nam lớn hơn 3” xảy ra thì biến cố P: “Trong 5 người được chọn, số nam không vượt quá 3” không xảy ra và ngược lại, nếu biến cố P xảy ra thì biến cố M không xảy ra.
Hay M ∩ P = ∅ nên biến cố M và biến cố P là xung khắc.
A: “Số chấm xuất hiện ở lần gieo thứ nhất lớn hơn 3”;
B: “Số chấm xuất hiện ở lần gieo thứ hai nhỏ hơn 3”;
C: “Số chấm xuất hiện ở lần gieo thứ ba lớn hơn 3”;
D: “Số chấm xuất hiện ở lần gieo thứ nhất nhỏ hơn 3”.
Trong các biến cố trên, tìm:
a) Một cặp biến cố xung khắc;
b) Ba cặp biến cố độc lập.
Lời giải:
a) Ta thấy: Nếu biến cố A: “Số chấm xuất hiện ở lần gieo thứ nhất lớn hơn 3” xảy ra thì biến cố D: “Số chấm xuất hiện ở lần gieo thứ nhất nhỏ hơn 3” không xảy ra và ngược lại, nếu biến cố D xảy ra thì biến cố A không xảy ra.
Hay A ∩ D = ∅ nên biến cố A và biến cố D là xung khắc.
b) Vì các lần gieo là độc lập, nên việc xảy ra của biến cố A: “Số chấm xuất hiện ở lần gieo thứ nhất lớn hơn 3” không làm ảnh hưởng đến xác suất xảy ra của biến cố B: “Số chấm xuất hiện ở lần gieo thứ hai nhỏ hơn 3” nên biến cố A và biến cố B là hai biến cố độc lập.
Tương tự ta có hai cặp biến cố độc lập khác là: A và C, B và C.
Bài 10 trang 18 SBT Toán 11 Tập 2: Tung một đồng xu cân đối và đồng chất hai lần liên tiếp.
a) Viết các kết quả thuận lợi của không gian mẫu Ω và hai biến cố A: “Có ít nhất một lần xuất hiện mặt sấp”, B: “ Có ít nhất một lần xuất hiện mặt ngửa”.
b) Viết các kết quả thuận lợi của mỗi biến cố A ∪ B, A ∩ B.
c) Tính P(A), P(B), P(A ∪ B), P(A ∩ B). Cho biết A và B có là hai biến cố xung khắc không; A và B có là hai biến cố độc lập không.
Lời giải:
a) Kí hiệu: S là mặt sấp, N là mặt ngửa.
Gọi Ω là không gian mẫu của phép thử “Tung một đồng xu cân đối và đồng chất liên tiếp hai lần”. Khi đó Ω = {SS; SN; NS; NN}.
Tập hợp các kết quả thuận lợi cho biến cố A là: A = {SS; SN; NS};
Tập hợp các kết quả thuận lợi cho biến cố B là: B = {NS; SN; NN}.
b) Các kết quả thuận lợi của biến cố A ∪ B là {SS; SN; NS; NN};
Các kết quả thuận lợi của biến cố A ∩ B là {SN; NS}.
c) Số phần tử của không gian mẫu là: n(Ω) = 4;
Ta có n(A) = 3, n(B) = 3, n(A ∪ B) = 4, n(A ∩ B) = 2.
Suy ra:
⦁
⦁
⦁
Vì A ∩ B ≠ ∅ (do ) nên biến cố A và biến cố B không là hai biến cố xung khắc.
Vì P(A ∩ B) ≠ P(A) . P(B) (do ) nên biến cố A và biến cố B không là hai biến cố độc lập.
Lời giải:
Ta có: P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Nên P(A ∩ B) = P(A) + P(B) – P(A ∪ B) = 0,4 + 0,5 – 0,6 = 0,3.
Suy ra A ∩ B ≠ ∅. Vậy A và B không là hai biến cố xung khắc.
Lời giải:
Ta có: 0,1 ≠ 0,3 . 0,4 hay P(A ∩ B) ≠ P(A) . P(B)
Vậy A và B không là hai biến cố độc lập.
Bài 13 trang 18 SBT Toán 11 Tập 2: Gieo một xúc xắc cân đối và đồng chất hai lần liên tiếp.
a) Không gian mẫu Ω có bao nhiêu phần tử?
b) Xét các biến cố:
A: “Số chấm xuất hiện ở lần gieo thứ nhất là 2”;
B: “Số chấm xuất hiện ở lần gieo thứ hai là 3”.
Tính xác suất của các biến cố A, B, A ∩ B.
Lời giải:
a) Số phần tử của không gian mẫu Ω là: n(Ω) = 6.6 = 36.
b) Xét biến cố A: “Số chấm xuất hiện ở lần gieo thứ nhất là 2”.
Lần gieo thứ nhất, số chấm xuất hiện là 2, có 1 cách.
Lần gieo thứ hai, số chấm xuất hiện có thể là 1; 2; 3; 4; 5; 6. Do đó có 6 cách.
Vậy số kết quả thuận lợi cho biến cố A là: n(A) = 1.6 = 6.
Suy ra:
Tương tự, số kết quả thuận lợi cho biến cố B là: n(B) = 6.1 = 6.
Suy ra:
Ta thấy: Vì hai lần gieo liên tiếp là độc lập nên xác suất của biến cố B khi biến cố A xảy ra là xác suất của biến cố B khi biến cố A không xảy ra cũng bằng
Do đó việc xảy ra hay không xảy ra của biến cố A không làm ảnh hướng đến xác suất của biến cố B. Tương tự, việc xảy ra hay không xảy ra của biến cố B không làm ảnh hướng đến xác suất của biến cố A. Vì vậy, hai biến cố A và B là độc lập.
Vậy
Tính xác suất của các biến cố: và
Lời giải:
Ta có:
Vì A và B là hai biến cố độc lập nên các cặp biến cố sau cũng độc lập: và B, A và và Suy ra:
a) M: “Bệnh nhân thứ nhất và bệnh nhân thứ hai đều bị biến chứng nặng”;
b) N: “Bệnh nhân thứ nhất không bị biến chứng nặng và bệnh nhân thứ hai bị biến chứng nặng”;
c) Q: “Bệnh nhân thứ nhất bị biến chứng nặng và bệnh nhân thứ hai không bị biến chứng nặng”;
d) R: “Bệnh nhân thứ nhất và bệnh nhân thứ hai đều không bị biến chứng nặng”;
e) S: “Có ít nhất một trong hai bệnh nhân bị biến chứng nặng”.
Lời giải:
Xét các biến cố A: “Bệnh nhân thứ nhất bị biến chứng nặng” và B: “Bệnh nhân thứ hai bị biến chứng nặng”. Khi đó P(A) = 0,2 và P(B) = 0,25.
Biến cố đối của biến cố A là “Bệnh nhân thứ nhất không bị biến chứng nặng”.
Suy ra
Biến cố đối của biến cố B là “Bệnh nhân thứ hai không bị biến chứng nặng”.
Suy ra
Từ giả thiết, ta có hai biến A và B là hai biến cố độc lập nên và B; A và và là các cặp biến cố độc lập.
a) Ta có M = A ∩ B nên P(M) = P(A ∩ B) = P(A) . P(B) = 0,2 . 0,25 = 0,05.
b) Do B là hai biến cố độc lập và
Nên
c) Do A, là hai biến cố độc lập và
Nên
d) Do là hai biến cố độc lập và
Nên
e) Ta thấy S là biến cố đối của biến cố R, nên P(S) = 1 – P(R) = 1 – 0,6 = 0,4.
a) A: “Học sinh được chọn thích chơi cầu lông”;
b) B: “Học sinh được chọn thích chơi bóng bàn”;
c) C: “Học sinh được chọn vừa thích chơi cầu lông vừa thích chơi bóng bàn”;
d) D: “Học sinh được chọn thích chơi ít nhất một trong hai môn thể thao là câu lông hoặc bóng bàn”.
Lời giải:
Mỗi cách chọn 1 học sinh từ 40 học sinh trong lớp cho ta một tổ hợp chập 1 của 40 phần tử. Do đó, không gian mẫu Ω gồm các tổ hợp chập 1 của 40 phần tử và
a) Xét biến cố A: “Học sinh được chọn thích chơi cầu lông”.
Số các kết quả thuận lợi cho biến cố A là
Xác suất của biến cố A là:
b) Số các kết quả thuận lợi cho biến cố B là
Xác suất của biến cố B là:
c) Số các kết quả thuận lợi cho biến cố C là
Xác suất của biến cố C là:
d) Ta thấy D = A ∪ B và C = A ∩ B nên ta có:
Lời giải:
Xét các biến cố A: “Van I hoạt động tốt” và B: “Van II hoạt động tốt”.
Từ giả thiết, suy ra A, B là hai biến cố độc lập và P(A) = 0,8; P(B) = 0,6.
Suy ra: P(A ∩ B) = P(A) . P(B) = 0,8 . 0,6 = 0,48.
Xét biến cố C: “Nồi cơm điện hoạt động an toàn”.
Theo đề bài, nồi cơm điện hoạt động an toàn khi có ít nhất một van hoạt động tốt hay C = A ∪ B.
Xác suất nồi cơm điện hoạt động an toàn là:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 0,8 + 0,6 – 0,48 = 0,92.
Lời giải:
Xét các biến cố M: “Xạ thủ A bắn trúng mục tiêu” và N: “Xạ thủ B bắn trúng mục tiêu”.
Từ giả thiết, ta có M, N là hai biến cố độc lập và P(M) = 0,6; P(N) = 0,65.
Xét các biến cố đối:
“Xạ thủ A không bắn trúng mục tiêu”;
“Xạ thủ A không bắn trúng mục tiêu”;
“Mục tiêu không bị hạ”.
Khi đó
và là hai biến cố độc lập
Do đó
Suy ra:
a) A: “Hai số được chọn là số chẵn”;
b) B: “Hai số được chọn là số lẻ”;
c) C: “Tổng của hai số được chọn là số chẵn”.
Lời giải:
Mỗi cách chọn ngẫu nhiên hai số khác nhau từ 21 số nguyên dương cho ta một tổ hợp chập 2 của 21 phần tử. Do đó, không gian mẫu Ω gồm các tổ hợp chập 2 của 21 phần tử và
a) Ta thấy trong 21 số nguyên dương đầu tiên có 10 số chẵn là: 2; 4; …; 20.
Suy ra số các kết quả thuận lợi cho biến cố A là
Xác suất của biến cố A là:
b) Ta thấy trong 21 số nguyên dương đầu tiên có 11 số lẻ là 1; 3; 5; …; 21.
Suy ra số các kết quả thuận lợi cho biến cố B là
Xác suất của biến cố B là:
c) Tổng của hai số được chọn là số chẵn khi hai số đó phải cùng chẵn hoặc cùng lẻ hay C = A ∪ B.
Ta có: A ∩ B = ∅ nên A và B là hai biến cố xung khắc.
Suy ra:
Lời giải:
Mỗi cách chọn ngẫu nhiên 3 sản phẩm từ 10 + 18 = 28 sản phẩm trong hộp cho ta một tổ hợp chập 3 của 28 phần tử. Do đó, không gian mẫu Ω gồm các tổ hợp chập 3 của 28 phần tử và
Sơ đồ hình cây biểu thị các khả năng thuận lợi cho biến cố A:
Số các kết quả thuận lợi cho biến cố A là
Xác suất của biến cố A là
Chú ý: Đối với bài toán này, ta có thể sử dụng biến cố đối của biến cố A là “Trong ba sản phẩm lấy được, chỉ có một loại sản phẩm”.
Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm
Bài 2: Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất
Bài 1: Phép tính lũy thừa với số mũ thực
Bài 3: Hàm số mũ. Hàm số lôgarit
Lý thuyết Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất
1. Phép toán trên các biến cố
a) Biến cố hợp
Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu . Đặt , ta có C là một biến cố và được gọi là biến cố hợp của hai biến cố A và B, kí hiệu là .
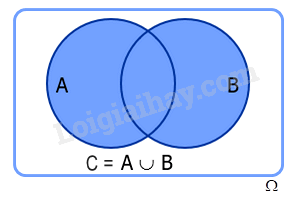
b) Biến cố giao
Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu . Đặt , ta có D là một biến cố và được gọi là biến cố giao của hai biến cố A và B, kí hiệu là hay AB.
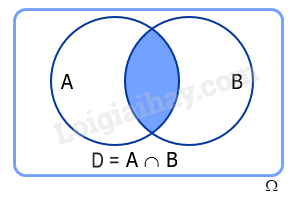
c) Biến cố xung khắc
Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu . Nếu thì A và B gọi là hai biến cố xung khắc.
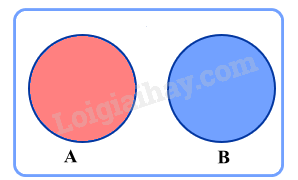
2. Biến cố độc lập
Cho hai biến cố A và B. Hai biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng đến xác suất xảy ra của biến cố kia.
Chú ý: Nếu A, B là hai biến cố độc lập thì mỗi cặp biến cố sau cũng độc lập: A và ; và B; và .
3. Các quy tắc tính xác suất
a) Công thức cộng xác suất
Cho hai biến cố A và B. Khi đó .
Hệ quả: Nếu hai biến cố A và B là xung khắc thì .
b) Công thức nhân xác suất
Cho hai biến cố A và B. Nếu hai biến cố A và B là độc lập thì .