Sách bài tập Toán 11 Bài 1 (Cánh diều): Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm

Admin Vietjack Ngày: 25-09-2024 Lớp 11

2.6 K

Với giải sách bài tập Toán 11 Bài 1: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 1: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm

Giải SBT Toán 11 trang 9

Bài 1 trang 8, 9 SBT Toán 11 Tập 2: Khi thống kê chiều cao của 40 bạn lớp 11A, ta thu được mẫu số liệu ghép nhóm cho ở Bảng 7 (đơn vị: centimét).

Nhóm	Tần số
[155 ; 160)	5
[160 ; 165)	12
[165 ; 170)	16
[170 ; 175)	7
	n = 40

Bảng 7

a) Độ dài của mỗi nhóm bằng:

A. 155;

B. 5;

C. 175;

D. 20.

b) Tần số của nhóm [160 ; 165) là bao nhiêu?

A. 5;

B. 16;

C. 12;

D. 7.

c) Nhóm có tần số lớn nhất là:

A. [155 ; 160);

B. [160 ; 165);

C. [165 ; 170);

D. [170 ; 175).

d) Giá trị cf₃ bằng:

A. 16;

B. 17;

C. 23;

D. 33.

e) Giá trị đại diện của nhóm [155 ; 160) bằng:

A. 157,5;

B. 155;

C. 160;

D. 5.

g) Nhóm có giá trị đại diện bằng 162,5 là:

A. [155 ; 160);

B. [160 ; 165);

C. [165 ; 170);

D. [170 ; 175).

Lời giải:

a) Đáp án đúng là: B

Độ dài của nhóm [155 ; 160) là 160 – 155 = 5

Tương tự: Độ dài của các nhóm [160 ; 165), [165 ; 170), [170 ; 175) là 5.

b) Đáp án đúng là: C

Tần số của nhóm [160 ; 165) là 12.

c) Đáp án đúng là: C

Tần số lớn nhất là 16 tương ứng với nhóm [165 ; 170).

d) Đáp án đúng là: D

Giá trị cf₃ là tần số tích lũy của nhóm 3 là nhóm [165 ; 170) bằng 5 + 12 + 16 = 33.

e) Đáp án đúng là: A

Giá trị đại diện của nhóm [155 ; 160) là $\frac{155 + 160}{2} = 157, 5$ .

g) Đáp án đúng là B

Ta có: $162, 5 = \frac{160 + 165}{2}$ nên nhóm có giá trị đại diện bằng 162,5 là [160 ; 165).

Bài 2 trang 9 SBT Toán 11 Tập 2: Xác định các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm như ở Bảng 7 (làm tròn cho các kết quả đến hàng phần mười).

Nhóm	Tần số
[155 ; 160)	5
[160 ; 165)	12
[165 ; 170)	16
[170 ; 175)	7
	n = 40

Bảng 7

Lời giải:

Bảng tần số ghép nhóm bao gồm giá trị đại diện và tần số tích lũy của mẫu số liệu được cho như sau:

Nhóm	Giá trị đại diện	Tần số	Tần số tích lũy
[155 ; 160)	157,5	5	5
[160 ; 165)	162,5	12	17
[165 ; 170)	167,5	16	33
[170 ; 175)	172,5	7	40
		n = 40

⦁ Số trung bình cộng là:

$\bar{x} = \frac{5 \cdot 157, 5 + 12 \cdot 162, 5 + 16 \cdot 167, 5 + 7 \cdot 172, 5}{40} \approx 165, 6.$

⦁ Ta có: $\frac{n}{2} = \frac{40}{2} = 20,$ $\frac{n}{4} = 10,$ $\frac{3 n}{4} = 30.$

Vì 17 < 20 < 33 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.

Xét nhóm 3 là nhóm [165; 170) có r = 165, d = 5, n₃ = 16 và nhóm 2 là nhóm [160; 165) có cf₂ = 17. Suy ra trung vị là:

$M_{e} = 165 + (\frac{20 - 17}{16}) \cdot 5 \approx 165, 9.$

Tứ phân vị thứ 2 là: Q₂ = M_e $\approx$ 165,9.

Vì 5 < 10 < 17 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.

Xét nhóm 2 là nhóm [160; 165) có s = 160, h = 5, n₂ = 12 và nhóm 1 là nhóm [155; 160) có cf₁ = 5.Suy ra tứ phân vị thứ nhất là:

$Q_{1} = 160 + (\frac{10 - 5}{12}) \cdot 5 \approx 162, 1.$

Vì 17 < 30 < 33 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.

Xét nhóm 3 là nhóm [165; 170) có t = 165, l = 5, n₃ = 16 và nhóm 2 là nhóm [160; 165) có cf₂ = 17. Suy ra tứ phân vị thứ ba là:

$Q_{3} = 165 + (\frac{30 - 17}{16}) \cdot 5 \approx 169, 1.$

⦁ Ta thấy nhóm 3 ứng với nửa khoảng [165; 170) là nhóm có tần số lớn nhất với u = 165, g = 5, n₃ = 16; nhóm 2 là nhóm [160; 165) có n₂ = 12 và nhóm 4 là nhóm [170; 175) có n₄ = 7. Suy ra mốt là:

$M_{O} = 165 + (\frac{16 - 12}{2 \cdot 16 - 12 - 7}) \cdot 5 \approx 166, 5.$

Bài 3 trang 9 SBT Toán 11 Tập 2: Cho mẫu số liệu ghép nhóm thống kế thời gian sử dụng điện thoại trước khi ngủ (đơn vị: phút) của một người trong 120 ngày như ở Bảng 8. Xác định các số đặc trưng đo xu thế trung tâm cho mẫu số liệu đó (làm tròn các kết quả đến hàng phần mười).

Nhóm	Tần số
[0 ; 4)	13
[4 ; 8)	29
[8 ; 12)	48
[12 ; 16)	22
[16 ; 20)	8
	n = 120

Bảng 8

Lời giải:

Bảng tần số ghép nhóm bao gồm giá trị đại diện và tần số tích lũy của mẫu số liệu được cho như sau:

Nhóm	Giá trị đại diện	Tần số	Tần số tích lũy
[0 ; 4)	2	13	13
[4 ; 8)	6	29	42
[8 ; 12)	10	48	90
[12 ; 16)	14	22	112
[16 ; 20)	18	8	120
		n = 120

⦁ Số trung bình cộng là:

$\bar{x} = \frac{13 \cdot 2 + 29 \cdot 6 + 48 \cdot 10 + 22 \cdot 14 + 8 \cdot 18}{120} \approx 9, 4.$

⦁ Ta có: $\frac{n}{2} = \frac{120}{2} = 60,$ $\frac{n}{4} = 30,$ $\frac{3 n}{4} = 90.$

Vì 42 < 60 < 90 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 60.

Xét nhóm 3 là nhóm [8 ; 12) có r = 8, d = 4, n₃ = 48 và nhóm 2 là nhóm [4 ; 8) có cf₂ = 42. Suy ra trung vị là:

$M_{e} = 8 + (\frac{60 - 42}{48}) \cdot 4 = 9, 5.$

Tứ phân vị thứ 2 là: Q₂ = M_e = 9,5

Vì 13 < 30 < 42 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.

Xét nhóm 2 là nhóm [4; 8) có s = 4, h = 4, n₂ = 29 và nhóm 1 là nhóm [0 ; 4) có cf₁ = 13. Suy ra tứ phân vị thứ nhất là:

$Q_{1} = 4 + (\frac{30 - 13}{29}) \cdot 4 \approx 6, 3.$

Vì 42 < 90 ≤ 90 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 90. Xét nhóm 3 là nhóm [8 ; 12) có t = 8, l = 4, n₃ = 48 và nhóm 2 là nhóm [4 ; 8) có cf₂ = 42. Suy ra tứ phân vị thứ ba là:

$Q_{3} = 8 + (\frac{90 - 42}{48}) \cdot 4 = 12.$

⦁ Ta thấy nhóm 3 ứng với nửa khoảng [8 ; 12) là nhóm có tần số lớn nhất với u = 8, g = 4, n₃ = 48; nhóm 2 là nhóm [4; 8) có n₂ = 29 và nhóm 4 là nhóm [12 ; 16) có n₄ = 22. Suy ra mốt là:

$M_{O} = 8 + (\frac{48 - 29}{2 \cdot 48 - 29 - 22}) \cdot 4 \approx 9, 7.$

Giải SBT Toán 11 trang 10

Bài 4 trang 9, 10 SBT Toán 11 Tập 2: Khi thống kê chỉ số đường huyết (đơn vị: mmol/L) của 28 người cao tuổi trong một lần đo, ta được kết quả sau:

Khi thống kê chỉ số đường huyết (đơn vị: mmol/L) của 28 người cao tuổi trong một lần đo

a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có năm nhóm ứng với năm nửa khoảng: [7,0 ; 7,2), [7,2 ; 7,4), [7,4 ; 7,6), [7,6 ; 7,8), [7,8 ; 8,0].

b) Độ dài của mỗi nhóm bằng:

A. 7;

B. 8;

C. 1;

D. 0,2.

c) Tần số của nhóm [7,8 ; 8,0] bằng:

A. 3;

B. 5;

C. 6;

D. 7.

d) Giá trị cf₃ bằng:

A. 7;

B. 13;

C. 20;

D. 25.

e) Giá trị đại diện của nhóm [7,4 ; 7,6) bằng:

A.7,4;

B. 7,6;

C. 7,5;

D. 2.

g) Nhóm có giá trị đại diện bằng 7,7 là:

A. [7,0 ; 7,2);

B. [7,2 ; 7,4);

C. [7,4 ; 7,6);

D. [7,6 ; 7,8).

Lời giải:

a) Bảng tần số ghép nhóm bao gồm cả tần số tích lũy được cho như bảng sau:

Nhóm	Tần số	Tần số tích lũy
[7,0 ; 7,2)	7	7
[7,2 ; 7,4)	6	13
[7,4 ; 7,6)	7	20
[7,6 ; 7,8)	5	25
[7,8 ; 8,0]	3	28
	n = 28

b) Đáp án đúng là: D

Độ dài của nhóm [7,0 ; 7,2) là 7,2 – 7,0 = 0,2.

Tương tự: Độ dài của các nhóm [7,2 ; 7,4), [7,4 ; 7,6), [7,6 ; 7,8), [7,8 ; 8,0] là 0,2.

c) Đáp án đúng là: A

Tần số của nhóm [7,8 ; 8,0] là 3.

d) Đáp án đúng là: C

Giá trị cf₃ là tần số tích lũy của nhóm 3 là nhóm [7,4 ; 7,6) là 20.

e) Đáp án đúng là: C

Giá trị đại diện của nhóm [7,4 ; 7,6) là $\frac{7, 4 + 7, 6}{2} = 7, 5$ .

g) Đáp án đúng là D

Ta có: $7, 7 = \frac{7, 6 + 7, 8}{2}$ nên nhóm có giá trị đại diện bằng 7,7 là [7,6 ; 7,8).

Bài 5 trang 10 SBT Toán 11 Tập 2: Với mẫu số liệu ghép nhóm thu được ở Bài 4, xác định các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm đó (làm tròn các kết quả đến hàng phần mười).

Lời giải:

Bảng tần số ghép nhóm bao gồm giá trị đại diện và tần số tích lũy của mẫu số liệu được cho như sau:

Nhóm	Giá trị đại diện	Tần số	Tần số tích lũy
[7,0 ; 7,2)	7,1	7	7
[7,2 ; 7,4)	7,3	6	13
[7,4 ; 7,6)	7,5	7	20
[7,6 ; 7,8)	7,7	5	25
[7,8 ; 8,0]	7,9	3	28
		n = 28

⦁ Số trung bình cộng là:

$\bar{x} = \frac{7 \cdot 7, 1 + 6 \cdot 7, 3 + 7 \cdot 7, 5 + 5 \cdot 7, 7 + 3 \cdot 7, 9}{28} \approx 7, 4.$

⦁ Ta có: $\frac{n}{2} = \frac{28}{2} = 14,$ $\frac{n}{4} = 7,$ $\frac{3 n}{4} = 21.$

Vì 13 < 24 < 20 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 14.

Xét nhóm 3 là nhóm [7,4 ; 7,6) có r = 7,4, d = 0,2, n₃ = 7 và nhóm 2 là nhóm [7,2 ; 7,4) có cf₂ = 13. Suy ra trung vị là:

$M_{e} = 7, 4 + (\frac{14 - 13}{7}) \cdot 0, 2 \approx 7, 4.$

Tứ phân vị thứ 2 là: Q₂ = M_e $\approx$ 7,4.

Vì 0 < 7 ≤ 7 nên nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 7.

Xét nhóm 1 là nhóm [7,0; 7,2) có s = 7,0, h = 0,2, n₁ = 7 và cf₀ = 0.

Suy ra tứ phân vị thứ nhất là:

$Q_{1} = 7, 0 + (\frac{7 - 0}{7}) \cdot 0, 2 \approx 7, 2.$

Vì 20 < 21 < 25 nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 21. Xét nhóm 4 là nhóm [7,6 ; 7,8) có t = 7,6, l = 0,2, n₄ = 5 và nhóm 3 là nhóm [7,4 ; 7,6) có cf₃ = 20. Suy ra tứ phân vị thứ ba là:

$Q_{3} = 7, 6 + (\frac{21 - 20}{5}) \cdot 0, 2 \approx 7, 6.$

⦁ Ta thấy nhóm 1 và nhóm 3 tương ứng với nửa khoảng [7,0 ; 7,2) và [7,4 ; 7,6) là nhóm có tần số lớn nhất nên ta có hai mốt là:

Nhóm 1 ứng với nửa khoảng [7,0 ; 7,2) là nhóm có tần số lớn nhất với u = 7,0, g = 0,2, n₁ = 7; n₀ = 0 và nhóm 2 là nhóm [7,2; 7,4) có n₂ = 6. Suy ra mốt thứ nhất là:

$M_{O} = 7, 0 + (\frac{7 - 0}{2.7 - 0 - 6}) \cdot 0, 2 \approx 7, 2;$

Nhóm 3 ứng với nửa khoảng [7,4 ; 7,6) là nhóm có tần số lớn nhất với u = 7,4, g = 0,2, n₃ = 7; và nhóm 2 là nhóm [7,2; 7,4) có n₂ = 6 và nhóm 4 là nhóm [7,6; 7,8) có n₄ = 5. Suy ra mốt thứ hai là:

$M_{O} = 7, 4 + (\frac{7 - 6}{2.7 - 6 - 5}) \cdot 0, 2 \approx 7, 5.$

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 1: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm

Bài 2: Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất

Bài tập cuối chương 5

Bài 1: Phép tính lũy thừa với số mũ thực

Bài 2: Phép tính lôgarit

Bài 3: Hàm số mũ. Hàm số lôgarit

Lý thuyết Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm

1. Mẫu số liệu ghép nhóm

a) Bảng tần số ghép nhóm

- Mẫu số liệu ghép nhóm là mẫu số liệu cho dưới dạng bảng tần số ghép nhóm.

- Mỗi nhóm số liệu gồm một số giá trị của mẫu số liệu được ghép nhóm theo một tiêu chí xác định có dạng [a; b), trong đó a là đầu mút trái, b là đầu mút phải. Độ dài nhóm là b – a.

- Tần số của một nhóm là số số liệu trong mẫu số liệu thuộc vào nhóm đó. Tần số của nhóm 1, nhóm 2, …, nhóm m kí hiệu lần lượt là n₁, n₂, …, n_m.

- Bảng tần số ghép nhóm được lập như ở bảng 1, trong đó mẫu liệu gồm n số liệu được chia thành m nhóm ứng với m nửa khoảng [a₁; a₂); [a₂; a₃); …;[a_m; a_m+1), ở đó

a₁ < a₂ < … < a_m < a_m+1 và n = n₁ + n₂ + … + n_m.

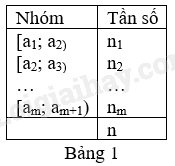
Lý thuyết Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm (Cánh diều 2024) hay, chi tiết | Toán lớp 11 (ảnh 1)

b) Ghép nhóm mẫu số liệu. Tần số tích lũy

Để chuyển mẫu số liệu không ghép nhóm thành mẫu số liệu ghép nhóm, ta thực hiện như sau:

- Chia miền giá trị của mẫu số liệu thành một số nhóm theo tiêu chí cho trước;

- Đếm số giá trị của mẫu số liệu thuộc mỗi nhóm (tần số) và lập bảng tần số ghép nhóm.

Chú ý: Khi ghép nhóm số liệu, ta thường phân chia các nhóm có độ dài bằng nhau và đầu mút của các nhóm có thể không phải là giá trị của mẫu số liệu. Nhóm cuối cùng có thể là [a_m; a_m+1].

- Tần số tích lũy của một nhóm là số số liệu trong mẫu số liệu có giá trị nhỏ hơn giá trị đầu mút phải của nhóm đó. Tần số tích lũy của nhóm 1, nhóm 2, …, nhóm m kí hiệu lần lượt là $c f_{1}, c f_{2}, . . ., c f_{m}$ .

- Bảng tần số ghép nhóm bao gồm cả tần số tích lũy được lập như ở Bảng 2.

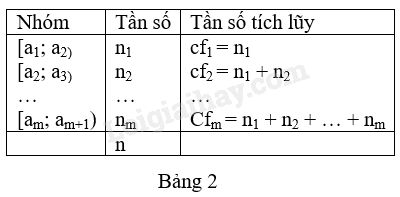
2. Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm

a) Số trung bình cộng

Cho mẫu số liệu ghép nhóm như ở bảng 3, trong đó giá trị đại diện của nhóm là trung điểm x_i của nửa khoảng (tính bằng trung bình cộng của hai đầu mút) ứng với nhóm i.

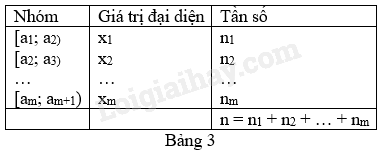
Lý thuyết Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm (Cánh diều 2024) hay, chi tiết | Toán lớp 11 (ảnh 4)

Số trung bình cộng của mẫu số liệu ghép nhóm, kí hiệu $\bar{x}$ , được tính theo công thức

$\bar{x} = \frac{n_{1} x_{1} + n_{2} x_{2} + . . . + n_{m} x_{m}}{n}$

b) Trung vị

Cho mẫu số liệu ghép nhóm bao gồm cả tần số tích lũy như ở Bảng 2.

Giả sử nhóm k là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{2}$ , tức là $c f_{k - 1} < \frac{n}{2}$ nhưng $c f_{k} \geq \frac{n}{2}$ . Ta gọi r, d, n_k lần lượt là đầu mút trái, độ dài, tần số của nhóm k; cf_k-1 là tần số tích lũy của nhóm k – 1.

Trung vị của mẫu số liệu ghép nhóm, kí hiệu M_e, được tính theo công thức sau:

$M_{e} = r + (\frac{\frac{n}{2} - c f_{k - 1}}{n_{k}}) . d$

Quy ước: cf₀ = 0.

c) Tứ phân vị

Cho mẫu số liệu ghép nhóm bao gồm cả tần số tích lũy như ở Bảng 2.

- Tứ phân vị thứ hai, kí hiệu Q₂, bằng trung vị M_e.

- Giả sử nhóm p là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{4}$ , tức là $c f_{p - 1} < \frac{n}{4}$ nhưng $c f_{p} \geq \frac{n}{4}$ . Ta gọi s, h, n_p lần lượt là đầu mút trái, độ dài, tần số của nhóm p; cf_p-1 là tần số tích lũy của nhóm p – 1.

Tứ phân vị thứ nhất, kí hiệu Q₁, được tính bằng công thức sau:

$Q_{1} = s + (\frac{\frac{n}{4} - c f_{p - 1}}{n_{p}}) . h$

- Giả sử nhóm q là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{3 n}{4}$ , tức là $c f_{q - 1} < \frac{3 n}{4}$ nhưng $c f_{q} \geq \frac{3 n}{4}$ . Ta gọi t, l, n_q lần lượt là đầu mút trái, độ dài, tần số của nhóm q; cf_q-1 là tần số tích lũy của nhóm q – 1.

Tứ phân vị thứ ba, kí hiệu Q₃, được tính bằng công thức sau:

$Q_{3} = t + (\frac{\frac{3 n}{4} - c f_{q - 1}}{n_{q}}) . l$

d) Mốt

Cho mẫu số liệu ghép nhóm như ở Bảng 1.

Giả sử nhóm i là nhóm có tần số lớn nhất. Ta gọi u, g, n_i lần lượt là đầu mút trái, độ dài, tần số của nhóm i; n_i-1, n_i-1 lần lượt là tần số của nhóm i – 1, nhóm i + 1.

Mốt của mẫu số liệu ghép nhóm, kí hiệu M_o, được tính theo công thức sau:

$M_{o} = u + (\frac{n_{i} - n_{i - 1}}{2 n_{i} - n_{i - 1} - n_{i + 1}}) . g$