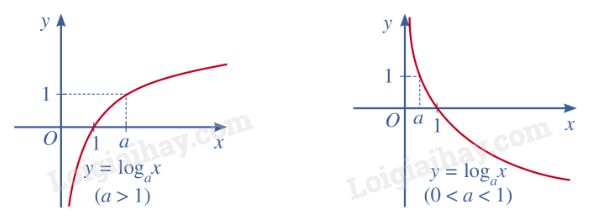Với giải sách bài tập Toán 11 Bài 3: Hàm số mũ. Hàm số lôgarit sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 3: Hàm số mũ. Hàm số lôgarit

Giải SBT Toán 11 trang 44

Bài 34 trang 44 SBT Toán 11 Tập 2: Tập xác định của hàm số y = 0,2^{x – 1} là:

A. ℝ \ {1};

B. ℝ;

C. (1; +∞);

D. (0; +∞).

Lời giải:

Đáp án đúng là: B

Tập xác định của hàm số mũ y = a^x (a > 0, a ≠ 1) là ℝ.

Ta thấy: a = 0,2 > 0 và a = 0,2 ≠ 1 nên tập xác định của hàm số y = 0,2^{x – 1} là ℝ.

Bài 35 trang 44 SBT Toán 11 Tập 2: Tập xác định của hàm số y = log₃(2x + 1) là:

A. ℝ;

B. $\left[-\frac{1}{2};+\infty \right);$

C. $\left(-\frac{1}{2};+\infty \right)\backslash \left\{0\right\};$

D. $\left(-\frac{1}{2};+\infty \right).$

Lời giải:

Đáp án đúng là: D

Điều kiện xác định: $2x+1>0\iff x>-\frac{1}{2}.$

Suy ra tập xác định của hàm số y = log₃(2x + 1) là $\left(-\frac{1}{2};+\infty \right).$

Bài 36 trang 44 SBT Toán 11 Tập 2: Tập xác định của hàm số y = log5(x2) là:

A. ℝ \ {0};

B. ℝ;

C. (0; +∞);

D. [0; +∞).

Lời giải:

Đáp án đúng là: A

Điều kiện xác định: x² > 0 ⇔ x ≠ 0.

Suy ra tập xác định của hàm số y = log₅(x²) là ℝ \ {0}.

Bài 37 trang 44 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số có tập xác định ℝ là:

A. y = log₅ x;

B. $y={\left(\sqrt{3}\right)}^x;$

C. y = ln(x² – 1);

D. $y=2^{\frac{1}{x}}.$

Lời giải:

Đáp án đúng là: B

Tập xác định của hàm số y = log₅x là (0; +∞).

Tập xác định của hàm số $y={\left(\sqrt{3}\right)}^x$ là ℝ.

Tập xác định của hàm số y = ln(x² – 1) là (–∞; –1) ∪ (1; +∞).

Tập xác định của hàm số $y=2^{\frac{1}{x}}$ là ℝ \ {0}.

Bài 38 trang 44 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số nghịch biến trên tập xác định của nó là:

A. y = e^x;

B. $y={\left(\frac{1}{5}\right)}^x;$

C. $y={\left(\sqrt{5}\right)}^x;$

D. $y={\left(1,2\right)}^x.$

Lời giải:

Đáp án đúng là: B

Cả 4 đáp án đều có tập xác định: D = ℝ.

Do $0<\frac{1}{5}<1$ nên hàm số $y={\left(\frac{1}{5}\right)}^x$ nghịch biến trên ℝ hay hàm số $y={\left(\frac{1}{5}\right)}^x$ nghịch biến trên tập xác định của nó.

Bài 39 trang 44 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số đồng biến trên tập xác định của nó là:

A. $y={\log }_{\frac{\sqrt{3}}{2}}x.$

B. y = log_0,5 x;

C. y = – logx;

D. y = lnx.

Lời giải:

Đáp án đúng là: D

Cả 4 đáp án đều có tập xác định: D = (0; +∞).

Do e > 1 nên hàm số y = lnx đồng biến trên D = (0; +∞) hay hàm số y = lnx đồng biến trên tập xác định của nó.

Bài 40 trang 44 SBT Toán 11 Tập 2: Giá trị thực của tham số a để hàm số y = log_2a+3 x đồng biến trên khoảng (0; +∞) là:

A. a > 1;

B. a > – 1;

C. a > 0, a ≠ 1;

D. a > –1; a ≠ 1.

Lời giải:

Đáp án đúng là: B

Để hàm số y = log_2a+3 x đồng biến trên khoảng (0; +∞) thì 2a + 3 > 1 ⇔ a > –1.

Bài 41 trang 44 SBT Toán 11 Tập 2: Cho $a^{\frac{7}{3}}<a^{\frac{7}{8}}$${\log }_b\left(\sqrt{2}+\sqrt{5}\right)<{\log }_b\left(\sqrt{2}+\sqrt{3}\right).$ Kết luận nào sau đây đúng?

A. a > 1 và b > 1;

B. 0 < a < 1 và 0 < b < 1;

C. 0 < a < 1 và b > 1;

D. a > 1 và 0 < b < 1.

Lời giải:

Đáp án đúng là: B

Do $a^{\frac{7}{3}}<a^{\frac{7}{8}}$$\frac{7}{3}>\frac{7}{8}$ nên 0 < a < 1.

Do ${\log }_b\left(\sqrt{2}+\sqrt{5}\right)<{\log }_b\left(\sqrt{2}+\sqrt{3}\right)$ và $\sqrt{2}+\sqrt{5}>\sqrt{2}+\sqrt{3}$ nên 0 < b < 1.

Vậy 0 < a < 1 và 0 < b < 1.

Giải SBT Toán 11 trang 45

Bài 42 trang 45 SBT Toán 11 Tập 2: Đường nào sau đây là đồ thị hàm số y = 4^x?

Lời giải:

Đáp án đúng là: D

Hàm số y = 4^x là hàm số mũ có a = 4 > 1 nên hàm số đồng biến trên ℝ. Do đó đồ thị ở phương án B và C là sai.

Thay x = 1 vào hàm số y = 4^x ta được y = 4¹ = 4, do đó đồ thị luôn đi qua điểm (1; 4). Do đó đồ thị ở phương án A là sai, đồ thị ở phương án D là đúng.

Vậy ta chọn phương án D.

Bài 43 trang 45 SBT Toán 11 Tập 2: Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit y = log_ax, y = log_bx, y = log_cx được cho bởi Hình 4. Kết luận nào sau đây là đúng đối với ba số a, b, c?

A. c > b > a;

B. a > b > c;

C. b > a > c;

D. c > a > b.

Lời giải:

Đáp án đúng là: C

Hàm số lôgarit y = log_c x nghịch biến trên (0; +∞) nên 0 < c < 1. (1)

Hàm số lôgarit y = log_ax, y = log_bx đồng biến trên (0; +∞) nên a > 1 và b > 1 (2)

Với x = 100, từ đồ thị ta thấy:

${\log }_{a}100>{\log }_{b}100>0$

$\iff \frac{1}{{\log }_{100}a}>\frac{1}{{\log }_{100}b}$

$\iff \frac{1}{{\log }_{100}a}>\frac{1}{{\log }_{100}b}$

$\iff {\log }_{100}a<{\log }_{100}b\iff a<b$ (do 100 > 1) (3)

Từ (1), (2) và (3) ta có: b > a > c.

Bài 44 trang 45 SBT Toán 11 Tập 2: Lập bảng biến thiên và vẽ đồ thị hàm số:

Lời giải:

a) Xét hàm số: $y={\left(\sqrt{2}\right)}^x$ có $\sqrt{2}>1$ nên ta có bảng biến thiên như sau:

Đồ thị của hàm số $y={\left(\sqrt{2}\right)}^x$ là một đường cong liền nét đi qua các điểm $\left(-2;\frac{1}{2}\right),$ (0; 1), (2; 2), ( ; 4) (hình vẽ dưới đây).

b) Xét hàm số: $y={\left(\frac{1}{\sqrt{2}}\right)}^x$có $\frac{1}{\sqrt{2}}<1$ nên ta có bảng biến thiên như sau:

Đồ thị của hàm số $y={\left(\frac{1}{\sqrt{2}}\right)}^x$ là một đường cong liền nét đi qua các điểm $\left(2;\frac{1}{2}\right)$, (0; 1), (–2; 2), (–4; 4) (hình vẽ dưới đây).

c) Xét hàm số: $y={\log }_{\sqrt{3}}x$ có $\sqrt{3}>1$ nên ta có bảng biến thiên như sau:

Đồ thị của hàm số $y={\log }_{\sqrt{3}}x$ là một đường cong liền nét đi qua các điểm $\left(\frac{1}{3};-2\right)$, (1; 0), (3; 2), (9; 4) (hình vẽ dưới đây).

d) Xét hàm số: $y=-{\log }_{2}x={\log }_{2^{-2}}x={\log }_{\frac{1}{2}}x$ có $0<\frac{1}{2}<1$ nên ta có bảng biến thiên như sau:

Đồ thị của hàm số y = –log₂x là một đường cong liền nét đi qua các điểm $\left(\frac{1}{2};1\right)$, (1; 0), (2; –1), (4; –2) (hình vẽ dưới đây).

Bài 45 trang 45 SBT Toán 11 Tập 2: Dựa vào đồ thị hàm số, cho biết với giá trị nào của x thì đồ thị hàm số y = (0,5)^x .

a) Nằm ở phía trên đường thẳng y = 1;

b) Nằm ở phía trên đường thẳng y = 4;

c) Nằm ở dưới trên đường thẳng $y=\frac{1}{2}.$

Lời giải:

Xét hàm số: y = (0,5)^x có 0 < 0,5 < 1 nên ta có bảng biến thiên như sau:

Đồ thị của hàm số y = (0,5)^x là một đường cong liền nét đi qua các điểm (–2; 4), (–1; 2), (0; 1), $\left(1;\frac{1}{2}\right)$ (hình vẽ dưới đây).

Dựa vào đồ thị hàm số trên ta thấy:

a) Đồ thị hàm số y = (0,5)^x nằm ở phía trên đường thẳng y = 1 khi x < 0.

b) Đồ thị hàm số y = (0,5)^x nằm ở phía trên đường thẳng y = 4 khi x < –2.

c) Đồ thị hàm số y = (0,5)^x nằm ở phía dưới đường thẳng $y=\frac{1}{2}$ khi x > 1.

Bài 46 trang 45 SBT Toán 11 Tập 2: Dựa vào đồ thị hàm số, cho biết với giá trị nào của x thì đồ thị hàm số y = log₃x:

a) Nằm ở phía trên đường thẳng y = 1;

b) Nằm ở phía dưới trục hoành.

Lời giải:

Xét hàm số: y = log₃x có 3 > 1 nên ta có bảng biến thiên như sau:

Đồ thị của hàm số y = log₃x là một đường cong liền nét đi qua các điểm $\left(\frac{1}{3};-1\right)$, (1; 0), (3; 1), (9; 2) (hình vẽ dưới đây).

Dựa vào đồ thị hàm số trên ta thấy:

a) Đồ thị hàm số y = log₃x nằm ở phía trên đường thẳng y = 1 khi x > 3.

b) Đồ thị hàm số y = log₃x nằm ở phía dưới trục hoành (y = 0) khi x < 1.

Giải SBT Toán 11 trang 46

Bài 47 trang 46 SBT Toán 11 Tập 2: Tìm tập xác định của các hàm số:

a) $y={\left(\frac{1}{2}\right)}^{2x-5};$ b) $y=3^{\frac{x-1}{x+1}};$

c) $y=1,5^{\sqrt{x+2}};$ d) y = log₅(1 – 5x);

e) y = log(4x² – 9); g) y = ln(x² – 4x + 4).

Lời giải:

a) Hàm số $y={\left(\frac{1}{2}\right)}^{2x-5}$ có tập xác định là ℝ.

b) Hàm số $y=3^{\frac{x-1}{x+1}}$ xác định khi x + 1 ≠ 0 hay x ≠ – 1.

Vậy tập xác định của hàm số $y=3^{\frac{x-1}{x+1}}$ là ℝ \ {–1}.

c) Hàm số $y=1,5^{\sqrt{x+2}}$ xác định khi x + 2 ≥ 0 hay x ≥ – 2.

Vậy tập xác định của hàm số $y=1,5^{\sqrt{x+2}}$ là [–2; +∞).

d) Hàm số y = log₅(1 – 5x) xác định khi 1 – 5x > 0 hay $x<\frac{1}{5}.$

Vậy tập xác định của hàm số $y={\log }_5\left(1-5x\right)$ là $x<\frac{1}{5}.$

e) Hàm số y = log(4x² – 9) xác định khi $4x^2–9>0\iff x^2>\frac{9}{4}\iff \left[\begin{array}{l}x>\frac{3}{2}\\ x<-\frac{3}{2}\end{array}\right..$

Vậy tập xác định của hàm số y = log(4x² – 9) là $\left(-\infty ;-\frac{3}{2}\right)\cup \left(\frac{3}{2};+\infty \right).$

g) Hàm số y = ln(x² – 4x + 4) xác định khi x² – 4x + 4 > 0 ⇔ (x – 2)² > 0 ⇔ x ≠ 2.

Vậy tập xác định của hàm số y = ln(x² – 4x + 4) là ℝ \ {2}.

Bài 48 trang 46 SBT Toán 11 Tập 2: Tìm tất cả giá trị của tham số m để hàm số y = log₃(4x² – 4x + m) xác định trên ℝ.

Lời giải:

Để hàm số y = log₃(4x² – 4x + m) xác định trên ℝ thì 4x² – 4x + m > 0, ∀x ∈ ℝ.

Đặt f(x) = 4x² – 4x + m

Có ∆’ = (−2)² – 4.m = 4 – 4m.

Để f(x) > 0, ∀x ∈ ℝ thì ∆’ < 0, ∀x ∈ ℝ ⟺ 4 – 4m < 0 ⟺ m > 1.

Vậy m > 1 thì hàm số y = log₃(4x² – 4x + m) xác định trên ℝ.

Bài 49 trang 46 SBT Toán 11 Tập 2: Tìm tất cả giá trị của tham số a để hàm số $y={\log }_{a^2-2a+1}x$ nghịch biến trên khoảng (0; +∞).

Lời giải:

Để hàm số $y={\log }_{a^2-2a+1}x$ nghịch biến trên khoảng (0; +∞) thì

$0<a^2-2a+1<1\iff \left\{\begin{array}{l}0<{\left(a-1\right)}^2\\ a^2-2a+1<1\end{array}\right.$

$\iff \left\{\begin{array}{l}a\ne 1\\ a^2-2a<0\end{array}\right.\iff \left\{\begin{array}{l}a\ne 1\\ 0<a<2\end{array}\right..$

Vậy a ∈ (0; 2) \ {1} thì hàm số $y={\log }_{a^2-2a+1}x$ nghịch biến trên khoảng (0; +∞).

Bài 50 trang 46 SBT Toán 11 Tập 2: Cho hàm số: $f\left(x\right)=\frac{9^x}{9^x+3}.$

a) Với a, b là hai số thực thỏa mãn a + b = 1. Tính f(a) + f(b).

b) Tính tổng: $S=f\left(\frac{1}{2023}\right)+f\left(\frac{2}{2023}\right)+\mathrm{...}+f\left(\frac{2022}{2023}\right).$

Lời giải:

a) Xét $f\left(x\right)=\frac{9^x}{9^x+3}.$

Ta có: $f\left(a\right)=\frac{9^a}{9^a+3}.$

Do a + b = 1 nên b = 1 – a.

Suy ra: $f\left(b\right)=f\left(1-a\right)=\frac{9^{1-a}}{9^{1-a}+3}=\frac{\frac{9}{9^a}}{\frac{9}{9^a}+3}$

$=\frac{\frac{9}{9^a}}{\frac{9+9^a\cdot 3}{9^a}}=\frac{9}{9+9^a\cdot 3}=\frac{3}{3+9^a}.$

Từ đó ta có: $f\left(a\right)+f\left(b\right)=\frac{9^a}{9^a+3}+\frac{3}{9^a+3}=\frac{9^a+3}{9^a+3}=1.$

b) Ta thấy: $\frac{1}{2023}+\frac{2022}{2023}=1;$$\frac{2}{2023}+\frac{2021}{2023}=1;$ …; $\frac{1011}{2023}+\frac{1012}{2023}=1.$

Nên theo câu a, ta có:

$f\left(\frac{1}{2023}\right)+f\left(\frac{2022}{2023}\right)=1;$

$f\left(\frac{2}{2023}\right)+f\left(\frac{2021}{2023}\right)=1;$

…;

$f\left(\frac{1011}{2023}\right)+f\left(\frac{1012}{2023}\right)=1.$

Suy ra:

$S=f\left(\frac{1}{2023}\right)+f\left(\frac{2}{2023}\right)+\mathrm{...}+f\left(\frac{2022}{2023}\right)$

$=\left[f\left(\frac{1}{2023}\right)+f\left(\frac{2022}{2023}\right)\right]+\left[f\left(\frac{2}{2023}\right)+f\left(\frac{2021}{2023}\right)\right]+\mathrm{...}$

$\mathrm{...}+\left[f\left(\frac{1011}{2023}\right)+f\left(\frac{1012}{2023}\right)\right]$ (có 1 011 nhóm)

= 1 + 1 + … + 1 (có 1 011 số hạng 1)

= 1 011.

Bài 51 trang 46 SBT Toán 11 Tập 2: Các nhà khoa học xác định được chu kì bán rã của ${}_6{}^{14}C$ là 5 730 năm, tức là sau 5 730 năm thì số nguyên tử ${}_6{}^{14}C$ giảm đi một nửa.

a) Gọi m₀ là khối lượng của ${}_6{}^{14}C$ tại thời điểm t = 0. Viết công thức tính khối lượng m(t) của ${}_6{}^{14}C$ tại thời điểm t (năm).

b) Một cây còn sống có lượng ${}_6{}^{14}C$ trong cây được duy trì không đổi. Nhưng nếu cây chết thì lượng ${}_6{}^{14}C$ trong cây phân rã theo chu kì bán rã của nó. Các nhà khảo cổ đã tìm thấy một mẫu gỗ cổ được xác định chết cách đây 2 000 năm. Tính tỉ lệ phần trăm lượng ${}_6{}^{14}C$ còn lại trong mẫu gỗ cổ đó so với lúc còn sinh trưởng (làm tròn kết quả đến hàng phần mười).

Lời giải:

a) Chu kì bán rã của ${}_6{}^{14}C$ là T = 5 730 (năm).

Cứ sau 5 730 năm thì số nguyên tử ${}_6{}^{14}C$ giảm đi một nửa hay sau 5 730 năm, khối lượng của ${}_6{}^{14}C$ giảm đi một nửa.

Suy ra khối lượng của ${}_6{}^{14}C$ còn lại sau t năm là: $m\left(t\right)=m_0\cdot {\left(\frac{1}{2}\right)}^{\frac{t}{5730}}.$

b) Từ công thức: $m\left(t\right)=m_0\cdot {\left(\frac{1}{2}\right)}^{\frac{t}{5730}},$ suy ra tỉ lệ phần trăm lượng ${}_6{}^{14}C$ còn lại trong mẫu gỗ cổ đó (t = 2 000) so với lúc còn sinh trưởng là:

$\frac{m\left(t\right)}{m_0}\cdot 100\%=\frac{m_0\cdot {\left(\frac{1}{2}\right)}^{\frac{t}{5730}}}{m_0}\cdot 100\%$

$={\left(\frac{1}{2}\right)}^{\frac{t}{5730}}\cdot 100\%={\left(\frac{1}{2}\right)}^{\frac{2000}{5730}}\cdot 100\%\approx 78,5\%.$

Bài 52 trang 46 SBT Toán 11 Tập 2: Mức cường độ âm L (dB) được tính bởi công thức $L=10\log \frac{I}{{10}^{-12}},$ trong đó I (W/m²) là cường độ âm. Tai người có thể nghe được âm có cường độ âm từ 10^–12 W/m² đến 10 W/m². Tính mức cường độ âm mà tai người có thể nghe được.

Lời giải:

Vì tai người có thể nghe được âm có cường độ âm từ 10^–12 W/m² đến 10 W/m² nên ta có:

Vậy mức cường độ âm mà tai người có thể nghe được 0 (dB) đến 130 (dB).

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác: