Với giải sách bài tập Toán 10 Bài tập cuối chương 2 sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài tập cuối chương 2
Giải SBT Toán 10 trang 34 Tập 1
A. Trắc nghiệm
A. 50x + 100y ≤ 900;
B. 50x + 100y ≥ 900;
C. 100x + 50y ≤ 900;
D. x + y = 900.
Lời giải:
Đáp án đúng là: A
Ta có x tờ tiền loại 50 nghìn đồng thì có giá trị là 50x (nghìn đồng).
y tờ tiền loại 100 nghìn đồng thì có giá trị là 100y (nghìn đồng).
Tổng số tiền bạn Danh trao tặng là: 50x + 100y (nghìn đồng).
Mà bạn Danh có 900 nghìn đồng nên 50x + 100y ≤ 900.
Vậy bất phương trình mô tả điều kiện ràng buộc đối với x, y là 50x + 100y ≤ 900.
A. 2x – 3y – 2022 ≤ 0;
B. 5x + y ≥ 2x + 11;
C. x + 2025 > 0;
D. .
Lời giải:
Đáp án đúng là: D
Xét đáp án A, 2x – 3y – 2022 ≤ 0 ⇔ 2x – 3y ≤ 2022, đây là một bất phương trình bậc nhất hai ẩn có dạng ax + by ≤ c (a, b, c là các số thực, a, b không đồng thời bằng 0).
Xét đáp án B, 5x + y ≥ 2x + 11 ⇔ 3x + y ≥ 11, đây là một bất phương trình bậc nhất hai ẩn có dạng ax + by ≥ c (a, b, c là các số thực, a, b không đồng thời bằng 0).
Xét đáp án C, x + 2025 > 0 ⇔ x + 0y > – 2025, đây là một bất phương trình bậc nhất hai ẩn có dạng ax + by > c (a, b, c là các số thực, a, b không đồng thời bằng 0).
Xét đáp án D, , đây không phải là một bất phương trình bậc nhất hai ẩn vì nó không có một trong các dạng ax + by < c, ax + by > c, ax + by ≤ c, ax + by ≥ c với a, b, c là các số thực, a, b không đồng thời bằng 0.
A. 2x + 3y < 6;
B. 2x + 3y > 6;
C. ;
D. .
Lời giải:
Đáp án đúng là: B
Đường thẳng d có dạng: y = ax + b.
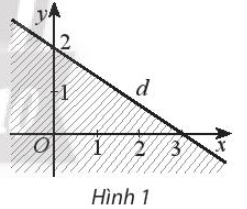
Từ Hình 1, ta thấy đường thẳng d đi qua hai điểm có tọa độ (3; 0) và (0; 2).
Do đó ta có:
Do đó d: y = + 2 ⇔ 3y = – 2x + 6 ⇔ 2x + 3y = 6.
Xét điểm O(0; 0) thuộc miền bị gạch chéo, ta có: 2 . 0 + 3 . 0 = 0 < 6.
Mà điểm O(0; 0) không thuộc miền nghiệm của bất phương trình ở Hình 1 nên bất phương trình cần tìm là 2x + 3y > 6 (không lấy dấu = vì miền nghiệm không kể bờ d).
Bài này đề sai, chờ sách bản cứng
A. ;
B. ;
C. ;
D.
Lời giải:
Đáp án đúng là:
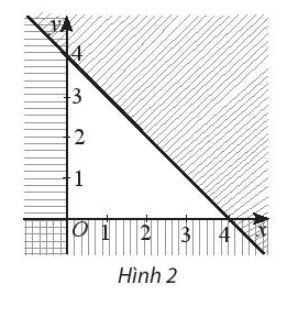
Từ Hình 2 ta thấy, miền tam giác không bị gạch chéo nằm phía trên trục Ox và bên phải trục Oy nên hệ phương trình có miền nghiệm như trên sẽ chứa hai bất phương trình x ≥ 0 và y ≥ 0. Hơn nữa đường thẳng đi qua hai điểm (0; 4) và (4; 0) có dạng x + y = 4 và điểm (1; 1) thuộc miền nghiệm của hệ bất phương trình cần tìm, mà 1 + 1 = 2 < 4, do đó ta có bất phương trình x + y ≤ 4.
Vậy ta có hệ bất phương trình cần tìm là
Giải SBT Toán 10 trang 35 Tập 1
A. – 48;
B. 0;
C. – 160;
D. – 40.
Lời giải:
Đáp án đúng là: A
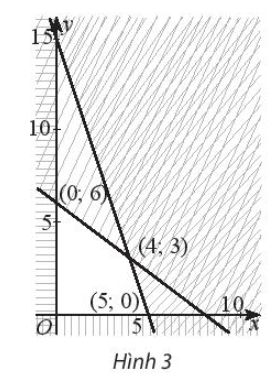
Miền đa giác không gạch chéo trong Hình 3 có tọa độ các đỉnh là (0; 0), (0; 6), (4; 3), (5; 0).
Người ta chứng minh được rằng biểu thức F = 2x – 8y đạt GTNN tại các đỉnh của đa giác.
Ta có: F(0; 0) = 2 . 0 – 8 . 0 = 0
F(0; 6) = 2 . 0 – 8 . 6 = – 48
F(4; 3) = 2 . 4 – 8 . 3 = – 16
F(5; 0) = 2 . 5 – 8 . 0 = 10
Vì – 48 < – 16 < 0 < 10.
Do đó, F đạt GTNN bằng – 48 tại đỉnh có tọa độ (0; 6).
A. 30;
B. 12;
C. 25;
D. 26.
Lời giải:
Đáp án đúng là: D
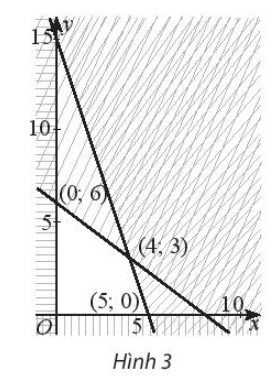
Miền đa giác không gạch chéo trong Hình 3 có tọa độ các đỉnh là (0; 0), (0; 6), (4; 3), (5; 0).
Người ta chứng minh được rằng biểu thức F = 5x + 2y đạt GTLN tại các đỉnh của đa giác.
Ta có: F(0; 0) = 5 . 0 + 2 . 0 = 0
F(0; 6) = 5. 0 + 2 . 6 = 12
F(4; 3) = 5 . 4 + 2 . 3 = 26
F(5; 0) = 5 . 5 + 2. 0 = 25
Vì 0 < 12 < 25 < 26.
Vậy F đạt GTLN bằng 26 tại đỉnh có tọa độ (4; 3).
B. Tự luận
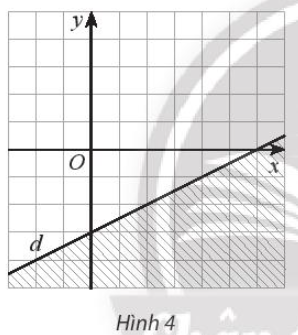
Lời giải:
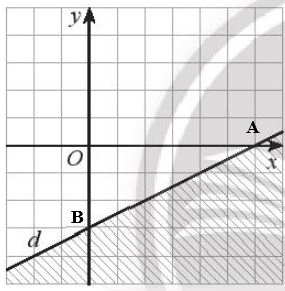
Gọi dạng đường thẳng d: y = ax + b.
Ta có đường thẳng d đi qua hai điểm A và B. Điểm A nằm trên tia Ox và cách O một khoảng bằng 6 cạnh ô vuông, do đó tọa độ A là A(6; 0). Điểm B nằm trên Oy và nằm phía dưới điểm O, cách O một khoảng 3 cạnh ô vuông nên B(0; – 3).
Khi đó ta có: .
Do đó d: y = x – 3 hay d: x – 2y – 6 = 0.
Xét điểm O(0; 0) thuộc miền nghiệm của bất phương trình cần tìm.
Ta có: 0 – 2 . 0 – 6 = – 6 < 0.
Do đó, bất phương trình cần tìm có dạng x – 2y – 6 ≤ 0 (do miền nghiệm bao gồm cả bờ d).
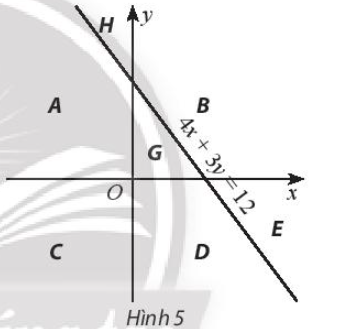
Lời giải:
Quan sát Hình 5, ta thấy miền B (kể cả bờ) nằm bên trên trục Ox (là miền nghiệm của bất phương trình y ≥ 0), bên phải trục Oy (là miền nghiệm của bất phương trình x ≥ 0) và không chứa điểm O(0; 0), lại có 4 . 0 + 3 . 0 = 0 < 12, do đó miền B nằm trong miền nghiệm của bất phương trình 4x + 3y ≥ 12.
Do đó, hệ bất phương trình có miền nghiệm là miền B là .
|
x |
0 |
0 |
1 |
1 |
2 |
2 |
4 |
|
y |
2 |
4 |
0 |
1 |
0 |
1 |
0 |
|
F = 4x + 5y |
|
|
|
|
|
|
|
|
G = 5x – 3y |
|
|
|
|
|
|
|
Trong các giá trị tìm được:
a) tìm GTLN của F.
Lời giải:
+ Với x = 0, y = 2, ta có: F = 4 . 0 + 5 . 2 = 10, G = 5 . 0 – 3 . 2 = – 6.
+ Với x = 0, y = 4, ta có: F = 4 . 0 + 5 . 4 = 20, G = 5 . 0 – 3 . 4 = – 12.
+ Với x = 1, y = 0, ta có: F = 4 . 1 + 5 . 0 = 4, G = 5 . 1 – 3 . 0 = 5.
+ Với x = 1, y = 1, ta có: F = 4 . 1 + 5 . 1 = 9, G = 5 . 1 – 3 . 1 = 2.
+ Với x = 2, y = 0, ta có: F = 4 . 2 + 5 . 0 = 8, G = 5 . 2 – 3 . 0 = 10.
+ Với x = 2, y = 1, ta có: F = 4 . 2 + 5 . 1 = 13, G = 5 . 2 – 3 . 1 = 7.
+ Với x = 4, y = 0, ta có: F = 4 . 4 + 5 . 0 = 16, G = 5 . 4 – 3 . 0 = 20.
Vậy ta hoàn thành được bảng như sau:
|
x |
0 |
0 |
1 |
1 |
2 |
2 |
4 |
|
y |
2 |
4 |
0 |
1 |
0 |
1 |
0 |
|
F = 4x + 5y |
10 |
20 |
4 |
9 |
8 |
13 |
16 |
|
G = 5x – 3y |
– 6 |
– 12 |
5 |
2 |
10 |
7 |
20 |
Từ bảng trên ta có:
a) GTLN của F là 20.
b) GTNN của G là – 12.
Giải SBT Toán 10 trang 36 Tập 1
Bài 4 trang 36 SBT Toán 10 Tập 1: Trên miền đa giác không gạch chéo ở Hình 6, hãy:
a) tìm GTLN của F = 2x + 3y;
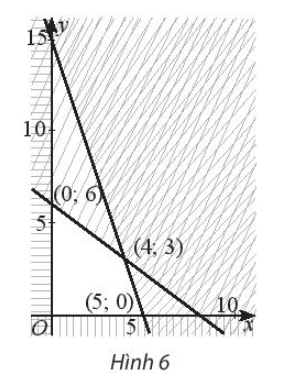
Lời giải:
Miền đa giác không gạch chéo ở Hình 6 có tọa độ các đỉnh là (0; 0), (0; 6), (4; 3) và (5; 0).
a) Người ta chứng minh được rằng biểu thức F = 2x + 3y đạt GTLN tại các đỉnh của đa giác không bị gạch trên Hình 6.
Ta có: F(0; 0) = 2 . 0 + 3 . 0 = 0
F(0; 6) = 2 . 0 + 3 . 6 = 18
F(4; 3) = 2 . 4 + 3 . 3 = 14
F(5; 0) = 2 . 5 + 3 . 0 = 10.
Vì 0 < 10 < 14 < 18 nên GTLN của F là 18 tại đỉnh có tọa độ (0; 6).
b) Người ta chứng minh được rằng biểu thức G = x – 4y đạt GTNN tại các đỉnh của đa giác không bị gạch trên Hình 6.
Ta có: G(0; 0) = 0 – 4 . 0 = 0
G(0; 6) = 0 – 4 . 6 = – 24
G(4; 3) = 4 – 4 . 3 = – 8
G(5; 0) = 5 – 4 . 0 = 5
Vì – 24 < – 8 < 0 < 5 nên GTNN của G là – 24 tại đỉnh có tọa độ (0; 6).
Lời giải:
Do x và y lần lượt là số sào đất bác Dũng dự định quy hoạch để trồng cà tím và cà chua nên x ≥ 0, y ≥ 0.
Để trồng x sào đất cà tím, cần số tiền mua hạt giống là 200 000x đồng.
Để trồng y sào đất cà chua, cần số tiền mua hạt giống là 100 000y đồng.
Vì bác Dũng chỉ có không quá 9 triệu đồng để mua hạt giống nên 200 000x + 100 000y ≤ 9 000 000 ⇔ 2x + y ≤ 90.
Vậy ta có hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y là .
Lời giải:
Vì x và y lần lượt là số chiếc máy tính cá nhân và máy tính bảng mà phân xưởng lắp ráp được trong một ngày nên x ≥ 0, y ≥ 0.
Do hạn chế về nhân công nên mỗi ngày chỉ có thể xuất xưởng tổng hai loại máy tính trên không quá 150 chiếc, do đó x + y ≤ 150.
Vậy ta có hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y là .
Lời giải:
Vì x và y lần lượt là số cá vàng và cá Koi bạn Hoàng dự định mua và trại cá chỉ bán mỗi loại cá từ 10 con trở lên nên x ≥ 10 và y ≥ 10.
Số tiền mua x con cá vàng là 35x (nghìn đồng).
Số tiền mua y con cá Koi là 150y (nghìn đồng).
Do Hoàng chỉ có 1,7 triệu đồng hay 1700 nghìn đồng nên 35x + 150y ≤ 1700 ⇔ 7x + 30y ≤ 340.
Vậy ta có hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y là .
Lời giải:
Gọi x và y lần lượt là số bình hoa loại nhỏ và loại lớn mà bạn học sinh có thể làm được (x ≥ 0, y ≥ 0).
Đổi 90 phút = 1,5 giờ.
Ban tổ chức yêu cầu phải làm ít nhất 12 bình hoa nên x + y ≥ 12.
Số giờ để làm x bình hoa loại nhỏ là x (giờ), số giờ để làm y bình hoa loại lớn là 1,5y (giờ).
Vì học sinh này chỉ thu xếp được 15 giờ nghỉ để làm nên x + 1,5y ≤ 15.
Do đó, ta có hệ bất phương trình sau: .
Biểu diễn miền nghiệm của hệ bất phương trình ta được miền tam giác ABC có tọa độ các đỉnh là A(12; 0), B(15; 0), C(6; 6) (phần không gạch chéo kể cả bờ trong hình dưới).
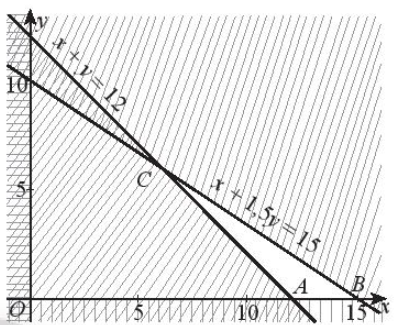
Số tiền gây quỹ là F = 100x + 200y.
Người ta chứng minh được rằng F đạt GTLN tại các đỉnh của tam giác ABC.
Ta có: F(12; 0) = 100 . 12 + 200 . 0 = 1 200
F(15; 0) = 100 . 15 + 200 . 0 = 1 500
F(6; 6) = 100 . 6 + 200 . 6 = 1 800.
Do đó, F đạt GTLN là 1 800 nghìn đồng tại đỉnh C(6; 6).
Vậy bạn đó cần làm 6 cái bình hoa mỗi loại để gây được quỹ nhiều tiền nhất.
Lời giải:
Gọi x và y lần lượt là số tấn sản phẩm X và Y mà xưởng cần sản xuất (x ≥ 0, y ≥ 0) (1).
Để sản xuất x tấn sản phẩm X cần 6x tấn nguyên liệu A, 2x tấn nguyên liệu B.
Để sản xuất y tấn sản phẩm Y cần 2y tấn nguyên liệu A, 2y tấn nguyên liệu B.
Do xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B nên 6x + 2y ≤ 12 và 2x + 2y ≤ 8.
Ta có 6x + 2y ≤ 12 ⇔ 3x + y ≤ 6. (2)
2x + 2y ≤ 8 ⇔ x + y ≤ 4. (3)
Từ đó ta có hệ bất phương trình sau: .
Biểu diễn miền nghiệm của hệ bất phương trình ta được miền tứ giác OABC có tọa độ các đỉnh là: O(0; 0), A(0; 4), B(1; 3), C(2; 0) (miền không bị gạch trong hình sau kể cả bờ).
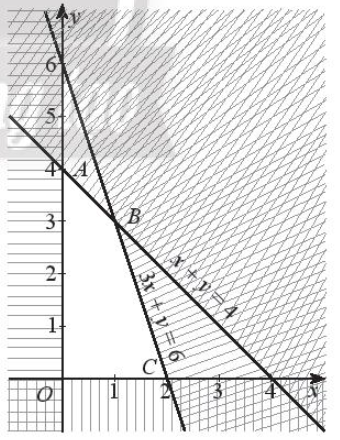
Số tiền lãi khi bán x sản phẩm X và y sản phẩm Y là F = 10x + 8y (triệu đồng).
Người ta chứng minh được rằng F đạt GTLN tại các đỉnh của tứ giác OABC.
Ta có: F(0; 0) = 10 . 0 + 8 . 0 = 0
F(0; 4) = 10 . 0 + 8 . 2 = 32
F(1; 3) = 10 . 1 + 8 . 3 = 34
F(2; 0) = 10 . 2 + 8 . 0 = 20
Do đó, F đạt GTLN là 34 triệu đồng tại đỉnh B(1; 3).
Vậy xưởng cần sản xuất 1 tấn sản phẩm X và 3 tấn sản phẩm Y thì sẽ có tổng tiền lãi cao nhất.
Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Hệ bất phương trình bậc nhất hai ẩn
Lý thuyết Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
1. Khái niệm bất phương trình bậc nhất hai ẩn
- Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng ax + by + c < 0; ax + by + c > 0; ax + by + c ≤ 0; ax + by + c ≥ 0,
trong đó a, b, c là những số cho trước, a, b không đồng thời bằng 0, x và y là các ẩn.
2. Nghiệm của bất phương trình bậc nhất hai ẩn
Xét bất phương trình ax + by + c < 0.
Mỗi cặp số (x0; y0) thỏa mãn ax0 + by0 + c < 0 được gọi là một nghiệm của bất phương trình đã cho.
Nghiệm của các bất phương trình ax + by + c > 0; ax + by + c ≤ 0; ax + by + c ≥ 0 được định nghĩa tương tự.
3. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn
- Trong mặt phẳng tọa độ Oxy, tập hợp các điểm (x0; y0) sao cho ax0 + by0 + c < 0 được gọi là miền nghiệm của bất phương trình ax + by + c < 0.
- Người ta chứng minh được: Mỗi phương trình ax + by + c = 0 (a, b không đồng thời bằng 0) xác định một đường thẳng ∆. Đường thẳng ∆ chia mặt phẳng tọa độ Oxy thành 2 nửa mặt phẳng, trong đó một nửa (không kể bờ ∆) là tập hợp các điểm (x; y) thỏa mãn ax + by + c > 0, nửa còn lại (không kể bờ ∆) là tập hợp các điểm (x; y) thỏa mãn ax + by + c < 0.
Ta có thể biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn ax + by + c < 0 như sau:
Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng ∆: ax + by +c = 0.
Bước 2: Lấy một điểm (x0; y0) không thuộc ∆. Tính ax0 + by0 + c.
+ Nếu ax0 + by0 + c < 0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) chứa điểm (x0; y0).
+ Nếu ax0 + by0 + c > 0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) không chứa điểm (x0; y0).
Chú ý: Đối với các bất phương trình bậc nhất hai ẩn dạng ax + by + c ≤ 0 (hoặc ax + by + c ≥ 0) thì miền nghiệm là miền nghiệm của bất phương trình ax + by + c < 0 (hoặc ax + by + c > 0) kể cả bờ.
4. Khái niệm hệ bất phương trình bậc nhất hai ẩn
- Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn x, y. Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho.
- Trên mặt phẳng tọa độ Oxy, tập hợp các điểm (x0; y0) có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn được gọi là miền nghiệm của hệ bất phương trình đó.
5. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ
Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ Oxy, ta thực hiện như sau:
- Trên cùng mặt phẳng tọa độ, biểu diễn miền nghiệm của mỗi bất phương trình của hệ.
- Phần giao của các miền nghiệm là miền nghiệm của hệ bất phương trình.
Chú ý: Miền mặt phẳng tọa độ bao gồm một đa giác lồi và phần nằm bên trong đa giác đó được gọi là một miền đa giác.
6. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của biểu thức F = ax + by trên một miền đa giác
Người ta chứng minh được F = ax + by đạt giá trị lớn nhất hoặc nhỏ nhất tại một trong các đỉnh của đa giác