Với lời giải SBT Toán 10 trang 35 Tập 1 chi tiết trong Bài tập cuối chương 2 sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài tập cuối chương 2 

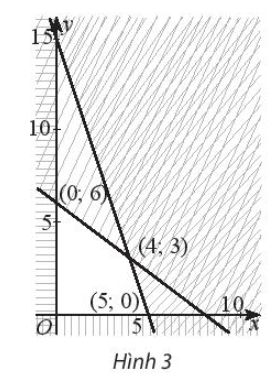
Bài 5 trang 35 SBT Toán 10 Tập 1: Biểu thức F = 2x – 8y đạt GTNN bằng bao nhiêu trên miền đa giác không gạch chéo trong Hình 3?

A. – 48;

B. 0;

C. – 160;

D. – 40.

Lời giải:

Đáp án đúng là: A

Miền đa giác không gạch chéo trong Hình 3 có tọa độ các đỉnh là (0; 0), (0; 6), (4; 3), (5; 0).

Người ta chứng minh được rằng biểu thức F = 2x – 8y đạt GTNN tại các đỉnh của đa giác.

Ta có: F(0; 0) = 2 . 0 – 8 . 0 = 0

F(0; 6) = 2 . 0 – 8 . 6 = – 48

F(4; 3) = 2 . 4 – 8 . 3 = – 16

F(5; 0) = 2 . 5 – 8 . 0 = 10

Vì – 48 < – 16 < 0 < 10.

Do đó, F đạt GTNN bằng – 48 tại đỉnh có tọa độ (0; 6). 

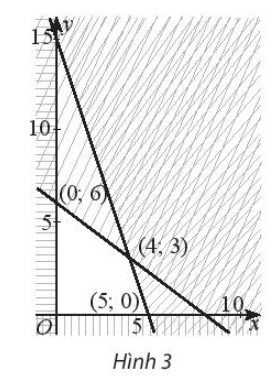
Bài 6 trang 35 SBT Toán 10 Tập 1: Biểu thức F = 5x + 2y đạt GTLN bằng bao nhiêu trên miền đa giác không gạch chéo trong Hình 3?

A. 30;

B. 12;

C. 25;

D. 26.

Lời giải:

Đáp án đúng là: D

Miền đa giác không gạch chéo trong Hình 3 có tọa độ các đỉnh là (0; 0), (0; 6), (4; 3), (5; 0).

Người ta chứng minh được rằng biểu thức F = 5x + 2y đạt GTLN tại các đỉnh của đa giác.

Ta có: F(0; 0) = 5 . 0 + 2 . 0 = 0

F(0; 6) = 5. 0 + 2 . 6 = 12

F(4; 3) = 5 . 4 + 2 . 3 = 26

F(5; 0) = 5 . 5 + 2. 0 = 25

Vì 0 < 12 < 25 < 26.

Vậy F đạt GTLN bằng 26 tại đỉnh có tọa độ (4; 3).

B. Tự luận

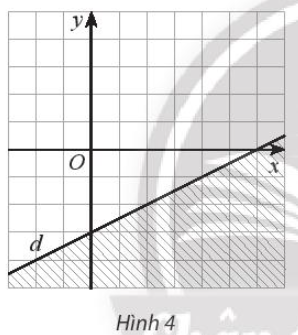
Bài 1 trang 35 SBT Toán 10 Tập 1: Tìm bất phương trình có miền nghiệm là miền không gạch chéo (kể cả bờ d) trong Hình 4 (mỗi ô vuông có cạnh là 1 đơn vị).

Lời giải:

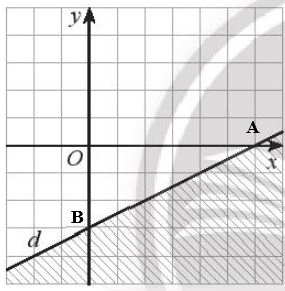
Gọi dạng đường thẳng d: y = ax + b.

Ta có đường thẳng d đi qua hai điểm A và B. Điểm A nằm trên tia Ox và cách O một khoảng bằng 6 cạnh ô vuông, do đó tọa độ A là A(6; 0). Điểm B nằm trên Oy và nằm phía dưới điểm O, cách O một khoảng 3 cạnh ô vuông nên B(0; – 3).

Khi đó ta có: $\left\{\begin{array}{l}0=6.a+b\\ -3=0.a+b\end{array}\right.\iff \left\{\begin{array}{l}a=\frac{1}{2}\\ b=-3\end{array}\right.$.

Do đó d: y = $\frac{1}{2}$x – 3 hay d: x – 2y – 6 = 0.

Xét điểm O(0; 0) thuộc miền nghiệm của bất phương trình cần tìm.

Ta có: 0 – 2 . 0 – 6 = – 6 < 0.

Do đó, bất phương trình cần tìm có dạng x – 2y – 6 ≤ 0 (do miền nghiệm bao gồm cả bờ d).

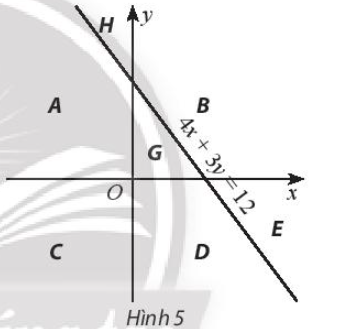
Bài 2 trang 35 SBT Toán 10 Tập 1: Đường thẳng 4x + 3y = 12 và hai trục tọa độ chia mặt phẳng Oxy thành các miền như Hình 5. Hãy tìm hệ bất phương trình có miền nghiệm là miền B (kể cả bờ).

Lời giải:

Quan sát Hình 5, ta thấy miền B (kể cả bờ) nằm bên trên trục Ox (là miền nghiệm của bất phương trình y ≥ 0), bên phải trục Oy (là miền nghiệm của bất phương trình x ≥ 0) và không chứa điểm O(0; 0), lại có 4 . 0 + 3 . 0 = 0 < 12, do đó miền B nằm trong miền nghiệm của bất phương trình 4x + 3y ≥ 12.

Do đó, hệ bất phương trình có miền nghiệm là miền B là $\left\{\begin{array}{l}4x+3y\ge 12\\ x\ge 0\\ y\ge 0\end{array}\right.$.

Bài 3 trang 35 SBT Toán 10 Tập 1: Tìm giá trị của F và G tương ứng với các giá trị x, y được cho trong bảng dưới đây.

 Trong các giá trị tìm được:

a) tìm GTLN của F.

b) tìm GTNN của G.

Lời giải:

+ Với x = 0, y = 2, ta có: F = 4 . 0 + 5 . 2 = 10, G = 5 . 0 – 3 . 2 = – 6.

+ Với x = 0, y = 4, ta có: F = 4 . 0 + 5 . 4 = 20, G = 5 . 0 – 3 . 4 = – 12.

+ Với x = 1, y = 0, ta có: F = 4 . 1 + 5 . 0 = 4, G = 5 . 1 – 3 . 0 = 5.

+ Với x = 1, y = 1, ta có: F = 4 . 1 + 5 . 1 = 9, G = 5 . 1 – 3 . 1 = 2.

+ Với x = 2, y = 0, ta có: F = 4 . 2 + 5 . 0 = 8, G = 5 . 2 – 3 . 0 = 10.

+ Với x = 2, y = 1, ta có: F = 4 . 2 + 5 . 1 = 13, G = 5 . 2 – 3 . 1 = 7.

+ Với x = 4, y = 0, ta có: F = 4 . 4 + 5 . 0 = 16, G = 5 . 4 – 3 . 0 = 20.

Vậy ta hoàn thành được bảng như sau:

 Từ bảng trên ta có:

a) GTLN của F là 20.

b) GTNN của G là – 12.

Xem thêm các bài giải sách bài tập Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 10 trang 34 Tập 1

Giải SBT Toán 10 trang 36 Tập 1

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài tập cuối chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai

Bài tập cuối chương 3