Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 21: Phương trình, bất phương trình mũ và lôgarit chi tiết sách Toán 11 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 21: Phương trình, bất phương trình mũ và lôgarit
V(t) = 780 ∙ (0,905)t.
Hỏi nếu theo mô hình này, sau bao nhiêu năm sử dụng thì giá trị của chiếc ô tô đó còn lại không quá 300 triệu đồng? (Làm tròn kết quả đến hàng đơn vị).
Lời giải:
Sau bài học, ta giải được bài toán trên như sau:
Theo yêu cầu bài ra, ta cần tìm t sao cho V(t) ≤ 300
⇔ 780 ∙ (0,905)t ≤ 300
.
Ta có 9,6 ≈ 10. Vậy sau khoảng 10 năm sử dụng thì giá trị của chiếc ô tô đó còn lại không quá 300 triệu đồng.
1. Phương trình mũ
HĐ1 trang 20 Toán 11 Tập 2: Nhận biết nghiệm phương trình mũ
Xét phương trình: .
a) Khi viết thành luỹ thừa của 2 thì phương trình trên trở thành phương trình nào?
b) So sánh số mũ của 2 ở hai vế của phương trình nhận được ở câu a để tìm x.
Lời giải:
a) Ta có . Khi đó phương trình đã cho trở thành
2x + 1 = 2– 2. (*)
b) Vì cơ số ở vế của (*) đều bằng nhau nên số mũ phải bằng nhau, tức là
x + 1 = – 2 ⇔ x = – 3.
Luyện tập 1 trang 21 Toán 11 Tập 2: Giải các phương trình sau:
a) ;
b) 2e2x = 5.
Lời giải:
a)
Đưa vế phải về cơ số 2, ta có .
Khi đó phương trình đã cho trở thành
23x – 1 = 2– x – 1 ⇔ 3x – 1 = – x – 1 ⇔ 4x = 0 ⇔ x = 0.
Vậy phương trình đã cho có nghiệm duy nhất x = 0.
b) 2e2x = 5 ⇔ e2x = .
Lấy lôgarit tự nhiên hai vế của phương trình trên ta được 2x = ln hay x = ln.
Vậy phương trình đã cho có nghiệm duy nhất x = ln.
2. Phương trình Lôgarit
HĐ2 trang 21 Toán 11 Tập 2: Nhận biết nghiệm của phương trình lôgarit
Xét phương trình: 2log2x = – 3.
a) Từ phương trình trên, hãy tính log2x.
b) Từ kết quả ở câu a và sử dụng định nghĩa lôgarit, hãy tìm x.
Lời giải:
a) Ta có 2log2x = – 3 .
b) Từ định nghĩa lôgarit ta có:
.
Luyện tập 2 trang 21 Toán 11 Tập 2: Giải các phương trình sau:
a) 4 – log(3 – x) = 3;
b) log2(x + 2) + log2(x – 1) = 1.
Lời giải:
a) 4 – log(3 – x) = 3
Điều kiện: 3 – x > 0 ⇔ x < 3.
Phương trình đã cho trở thành log(3 – x) = 1 ⇔ 3 – x = 101 ⇔ x = – 7 (t/m).
Vậy phương trình đã cho có nghiệm duy nhất x = – 7.
b) log2(x + 2) + log2(x – 1) = 1
Áp dụng tính chất của lôgarit, phương trình đã cho trở thành
log2 [(x + 2)(x – 1)] = 1
⇔ (x + 2)(x – 1) = 21
⇔ x2 + x – 2 = 2
⇔ x2 + x – 4 = 0
Kết hợp với điều kiện, vậy phương trình đã cho có nghiệm duy nhất .
3. Bất phương trình mũ
Giải Toán 11 trang 22 Tập 2
HĐ3 trang 22 Toán 11 Tập 2: Nhận biết nghiệm của bất phương trình mũ
Cho đồ thị của các hàm số y = 2x và y = 4 như Hình 6.7. Tìm khoảng giá trị của x mà đồ thị hàm số y = 2x nằm phía trên đường thẳng y = 4 và từ đó suy ra tập nghiệm của bất phương trình 2x > 4.
Lời giải:
Quan sát đồ thị Hình 6.7, ta thấy khoảng giá trị của x mà đồ thị hàm số y = 2x nằm phía trên đường thẳng y = 4 là (2; + ∞).
Vậy tập nghiệm của bất phương trình 2x > 4 là (2; + ∞).
Luyện tập 3 trang 23 Toán 11 Tập 2: Giải các bất phương trình sau:
a) 0,12x – 1 ≤ 0,12 – x;
b) 3 ∙ 2x + 1 ≤ 1.
Lời giải:
a) Ta có:
0,12x – 1 ≤ 0,12 – x
⇔ 2x – 1 ≥ 2 – x (do 0 < 0,1 < 1)
⇔ 3x ≥ 3
⇔ x ≥ 1.
Vậy tập nghiệm của bất phương trình đã cho là [1; + ∞).
b) 3 ∙ 2x + 1 ≤ 1
(do 2 > 1)
⇔ x ≤ log23– 1 – 1
⇔ x ≤ – log23 – log22
⇔ x ≤ – log2(3 ∙ 2)
⇔ x ≤ – log26
Vậy tập nghiệm của bất phương trình đã cho là (– ∞; – log26].
4. Bất phương trình Lôgarit
HĐ4 trang 23 Toán 11 Tập 2: Nhận biết nghiệm của bất phương trình lôgarit
Cho đồ thị của các hàm số y = log2x và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số y = log2x nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình log2 x > 2.
Lời giải:
Quan sát đồ thị ở Hình 6.8, ta thấy khoảng giá trị của x mà đồ thị hàm số y = log2x nằm phía trên đường thẳng y = 2 là (4; + ∞).
Vậy tập nghiệm của bất phương trình log2 x > 2 là (4; + ∞).
Luyện tập 4 trang 24 Toán 11 Tập 2: Giải các bất phương trình sau:
a) ;
b) 2log(2x + 1) > 3.
Lời giải:
a)
Bất phương trình đã cho tương đương với
⇔ – log7(x + 1) > log7(2 – x)
⇔ log7(x + 1)– 1 > log7(2 – x)
⇔ (x + 1)– 1 > 2 – x (do 7 > 1).
(*)
Mà – 1 < x < 2 nên x + 1 > 0, do đó (*) ⇔ x2 – x – 1 > 0
Kết hợp với điều kiện ta được
Vậy tập nghiệm của bất phương trình đã cho là .
b) 2log(2x + 1) > 3
Điều kiện: 2x + 1 > 0 ⇔ x > .
Bất phương trình đã cho tương đương với
.
Kết hợp với điều kiện, vậy tập nghiệm của bất phương trình đã cho là .
.
(Theo britannica.com)
a) Tính áp suất khí quyển ở độ cao 4 km.
b) Ở độ cao trên 10 km thì áp suất khí quyển sẽ như thế nào?
Lời giải:
a) Ở độ cao 4 km, tức h = 4, thay vào công thức đã cho ta được
.
Vậy áp suất khí quyển ở độ cao 4 km khoảng 56,47 kPa.
b) Ở độ cao trên 10 km, tức h > 10, khi đó ta có
.
Vậy ở độ cao trên 10 km thì áp suất khí quyển nhỏ hơn 23,97 kPa.
Bài tập
Bài 6.20 trang 24 Toán 11 Tập 2: Giải các phương trình sau:
a) 3x – 1 = 27;
b) ;
c) ;
d) 5x = 32x – 1.
Lời giải:
a) 3x – 1 = 27
⇔ 3x – 1 = 33
⇔ x – 1 = 3
⇔ x = 4
Vậy phương trình đã cho có nghiệm duy nhất là x = 4.
b)
⇔ 4x2 – 6 = – 2x2 + 18
⇔ 6x2 = 24
⇔ x2 = 4
⇔ x = ± 2.
Vậy tập nghiệm của phương trình đã cho là S = {– 2; 2}.
c)
.
Vậy phương trình đã cho có nghiệm duy nhất là .
d) 5x = 32x – 1
Lấy lôgarit cơ số 3 hai vế của phương trình ta được
log35x = log332x – 1
⇔ x log35 = 2x – 1
⇔ (2 – log35)x = 1
⇔ x = .
Vậy phương trình đã cho có nghiệm duy nhất là x = .
Bài 6.21 trang 24 Toán 11 Tập 2: Giải các phương trình sau:
a) log(x + 1) = 2;
b) 2log4x + log2(x – 3) = 2;
c) lnx + ln(x – 1) = ln4x;
d) log3(x2 – 3x + 2) = log3(2x – 4).
Lời giải:
a) log(x + 1) = 2
Điều kiện: x + 1 > 0 ⇔ x > – 1.
Phương trình đã cho tương đương với x + 1 = 102 ⇔ x = 100 – 1 ⇔ x = 99 (t/m).
Vậy phương trình đã cho có nghiệm duy nhất x = 99.
b) 2log4x + log2(x – 3) = 2
Ta có 2log4x + log2(x – 3) = 2
⇔ log2x + log2(x – 3) = 2
⇔ log2x(x – 3) = 2
⇔ x(x – 3) = 22
⇔ x2 – 3x – 4 = 0
⇔ x = – 1 hoặc x = 4.
Kết hợp với điều kiện, vậy phương trình đã cho có nghiệm duy nhất x = 4.
c) lnx + ln(x – 1) = ln4x
Ta có: lnx + ln(x – 1) = ln4x
⇔ lnx(x – 1) = ln4x
⇔ x(x – 1) = 4x
⇔ x2 – 5x = 0
⇔ x(x – 5) = 0
⇔ x = 0 hoặc x = 5.
Kết hợp với điều kiện, vậy phương trình đã cho có nghiệm duy nhất x = 5.
d) log3(x2 – 3x + 2) = log3(2x – 4)
Phương trình đã cho tương đương với
x2 – 3x + 2 = 2x – 4
⇔ x2 – 5x + 6 = 0
⇔ x = 2 hoặc x = 3.
Kết hợp với điều kiện, vậy phương trình đã cho có nghiệm duy nhất x = 3.
Bài 6.22 trang 24 Toán 11 Tập 2: Giải các bất phương trình sau:
a) 0,12 – x > 0,14 + 2x;
b) 2 . 52x + 1 ≤ 3;
c) log3(x + 7) ≥ – 1;
d) log0,5(x + 7) ≥ log0,5(2x – 1).
Lời giải:
a) 0,12 – x > 0,14 + 2x
⇔ 2 – x < 4 + 2x (do 0 < 0,1 < 1)
⇔ 3x > – 2
⇔ x > .
Vậy tập nghiệm của bất phương trình đã cho là .
b) 2 . 52x + 1 ≤ 3
.
Vậy tập nghiệm của bất phương trình đã cho là .
c) log3(x + 7) ≥ – 1
Điều kiện: x + 7 > 0 ⇔ x > – 7.
Ta có: log3(x + 7) ≥ – 1
⇔ x + 7 ≥ 3– 1
⇔ x ≥
.
Kết hợp với điều kiện, vậy tập nghiệm của bất phương trình đã cho là .
d) log0,5(x + 7) ≥ log0,5(2x – 1)
Ta có: log0,5(x + 7) ≥ log0,5(2x – 1)
⇔ x + 7 ≤ 2x – 1 (do 0 < 0,5 < 1)
⇔ x ≥ 8.
Kết hợp với điều kiện, vậy tập nghiệm của bất phương trình đã cho là S = [8; + ∞).
A = 500 ∙ (1 + 0,075)n (triệu đồng).
Tính thời gian tối thiểu gửi tiết kiệm để bác Minh thu được ít nhất 800 triệu đồng (cả vốn lẫn lãi).
Lời giải:
Số tiền bác Minh nhận được sau n năm gửi tiết kiệm là
A = 500 ∙ (1 + 0,075)n = 500 ∙ 1,075n (triệu đồng).
Để có được 800 triệu đồng thì A = 800
⇔ 500 ∙ 1,075n = 800 ⇔ 1,075n = 1,6 ⇔ n = log1,0751,6 ≈ 6,5.
Vậy sau khoảng 7 năm gửi tiết kiệm thì bác An thu được ít nhất 800 triệu đồng (cả vốn lẫn lãi).
N(t) = 500e0,4t.
Hỏi sau bao nhiêu giờ nuôi cấy, số lượng vi khuẩn vượt mức 80 000 con?
Lời giải:
Số lượng vi khuẩn vượt mức 80 000 con khi N(t) > 80 000
⇔ 500e0,4t > 80 000 ⇔ e0,4t > 160 ⇔ 0,4t > ln160 ⇔ t > ≈ 12,69.
Vậy sau khoảng 12,69 giờ nuôi cấy, số lượng vi khuẩn vượt mức 80 000 con.
a) Tìm nhiệt độ ban đầu của vật.
b) Sau bao lâu nhiệt độ của vật còn lại 30 ℃.
Lời giải:
a) Nhiệt độ ban đầu T0 của vật ứng với nhiệt độ tại thời điểm t = 0, từ đó ta được
T0 = 25 + 70e– 0,5 ∙ 0 = 95 (℃).
Vậy nhiệt độ ban đầu của vật là 95 ℃.
b) Nhiệt độ của vật còn lại 30 ℃, tức T = 30, khi đó t thỏa mãn phương trình
25 + 70e– 0,5t = 30 .
Vậy sau khoảng 5,28 phút nhiệt độ của vật còn lại 30 ℃.
Lời giải:
Ta có: pH = – log[H+] = 8. Suy ra [H+] = 10– 8 (mol/lít).
Vậy nồng độ ion hydrogen của dung dịch có độ pH là 8 là 10– 8 mol/lít.
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 22: Hai đường thẳng vuông góc
Bài 23: Đường thẳng vuông góc với mặt phẳng
Lý thuyết Phương trình, bất phương trình mũ và lôgarit
1. Phương trình mũ
Phương trình mũ cơ bản có dạng (với ).
- Nếu b > 0 thì phương trình có nghiệm duy nhất .
- Nếu b 0 thì phương trình vô nghiệm.
Minh họa bằng đồ thị:
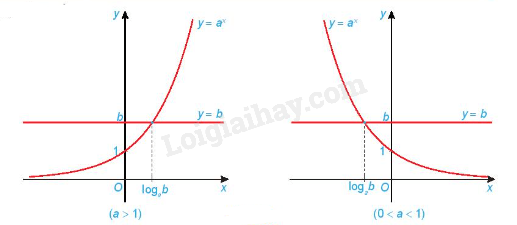
Chú ý: Phương pháp giải phương trình mũ bằng cách đưa về cùng cơ số:
Nếu thì .
2. Phương trình lôgarit
Phương trình lôgarit cơ bản có dạng .
Phương trình lôgarit cơ bản có nghiệm duy nhất .
Minh họa bằng đồ thị:
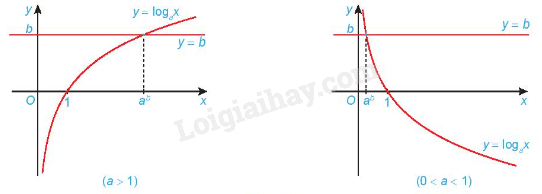
Chú ý: Phương pháp giải phương trình lôgarit bằng cách đưa về cùng cơ số:
Nếu và thì .
3. Bất phương trình mũ
Bất phương trình mũ cơ bản có dạng (hoặc ) với .
Xét bất phương trình dạng :
- Nếu thì tập nghiệm của bất phương trình là .
- Nếu b > 0 thì bất phương trình tương đương với .
Với a > 1, nghiệm của bất phương trình là .
Với , nghiệm của bất phương trình là .
Chú ý:
a) Các bất phương trình mũ cơ bản còn lại được giải tương tự.
b) Nếu a > 1 thì .
Nếu 0 < a < 1 thì .
4. Bất phương trình lôgarit
Bất phương trình lôgarit cơ bản có dạng (hoặc ) với .
Xét bất phương trình dạng :
- Nếu a > 1 thì nghiệm của bất phương trình là .
- Nếu 0 < a < 1 thì nghiệm của bất phương trình là .
Chú ý:
a) Các bất phương trình lôgarit cơ bản còn lại được giải tương tự.
b) Nếu a > 1 thì .
Nếu 0 < a < 1 thì .