Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 23: Đường thẳng vuông góc với mặt phẳng chi tiết sách Toán 11 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 23: Đường thẳng vuông góc với mặt phẳng

1. Đường thẳng vuông góc với mặt phẳng

Giải Toán 11 trang 31 Tập 2

HĐ1 trang 31 Toán 11 Tập 2: Đối với cánh cửa như trong Hình 7.10, khi đóng – mở cánh cửa, ta coi mép dưới BC của cánh cửa luôn sát sàn nhà (khe hở không đáng kể).

a) Từ quan sát trên, hãy giải thích vì sao đường thẳng AB vuông góc với mọi đường thẳng đi qua B trên sàn nhà.

b) Giải thích vì sao đường thẳng AB vuông góc với mọi đường thẳng trên sàn nhà.

Lời giải:

a) Trong quá trình đóng – mở cửa, đường thẳng AB cố định vì luôn đi qua hai bản lề cố định, đường thẳng BC trên sàn luôn đi qua điểm B cố định (B là giao của đường thẳng AB và mặt sàn). Vì đường thẳng BC quay quanh điểm B và (AB, BC) = 90° nên AB vuông góc với các đường thẳng trên mặt sàn và đi qua B.

b) Lấy đường thẳng a bất kì trên mặt sàn. Xét a' là đường thẳng trên mặt sàn, đi qua B và song song với a. Khi đó (AB, a) = (AB, a') = 90°.

Giải Toán 11 trang 32 Tập 2

Câu hỏi trang 32 Toán 11 Tập 2: Nếu đường thẳng ∆ và mặt phẳng (P) vuông góc với nhau thì chúng có cắt nhau hay không?

Lời giải:

Nếu đường thẳng ∆ và mặt phẳng (P) vuông góc với nhau thì chúng có cắt nhau.

Vì nếu trái lại thì ∆ song song hoặc nằm trên (P). Khi đó, có đường thẳng a thuộc (P) và song song với ∆. Do đó (∆, a) = 0°, điều này mâu thuẫn với giả thiết ∆ vuông góc  với (P).

HĐ2 trang 32 Toán 11 Tập 2: Gấp tấm bìa cứng hình chữ nhật sao cho nếp gấp chia tấm bìa thành hai hình chữ nhật, sau đó đặt nó lên mặt bàn như Hình 7.11.

a) Bằng cách trên, ta tạo đường thẳng AB vuông góc với hai đường thẳng nào thuộc mặt bàn?

b) Trên mặt bàn, qua điểm A kẻ một đường thẳng a tùy ý. Dùng ê ke, hãy kiểm tra trên mô hình xem AB có vuông góc với a hay không.

Lời giải:

a) Vì ABCD và ABMN là hình chữ nhật nên AB ^ AD, AB ^ AN.

b) Trong mô hình, đặt ê ke như mô tả trong hình vẽ ta thấy một cạnh của ê ke trùng với AB và một cạnh thuộc a nên AB vuông góc với a.

Câu hỏi trang 32 Toán 11 Tập 2: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì đường thẳng đó có vuông góc với cạnh còn lại hay không?

Lời giải:

Vì đường thẳng vuông góc với hai cạnh của một tam giác nên đường thẳng đó vuông góc với mặt phẳng chứa tam giác. Do đó đường thẳng đó vuông góc với cạnh còn lại của tam giác.

Luyện tập 1 trang 32 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, SA = SC và SB = SD (H.7.14). Chứng minh rằng $SO\perp \left(ABCD\right)$.

Lời giải:

Do O là tâm của hình bình hành ABCD nên O là trung điểm của AC, BD.

Xét tam giác SAC có SA = SC nên tam giác SAC cân tại S mà SO là trung tuyến nên SO là đường cao hay SO ^ AC.

Xét tam giác SBD có SB = SD nên tam giác SBD cân tại S mà SO là trung tuyến nên SO là đường cao hay SO ^ BD.

Vì  SO ^ AC và SO ^ BD nên SO ^ (ABCD).

Giải Toán 11 trang 33 Tập 2

Vận dụng trang 33 Toán 11 Tập 2:Khi làm cột treo quần áo, ta có thể tạo hai thanh đế thẳng đặt dưới sàn nhà và dựng cột treo vuông góc với hai thanh đế đó (H.7.15). Hãy giải thích vì sao bằng cách đó ta có được cột treo vuông góc với sàn nhà.

Lời giải:

Ta coi hai thanh đế thẳng đặt dưới sàn nhà là hai đường thẳng cắt nhau và sàn nhà là một mặt phẳng.

Vì cột treo vuông góc với hai thanh đế (cắt nhau) nên cột vuông góc với sàn nhà (chứa hai thanh đế).

2. Tính chất

HĐ3 trang 33 Toán 11 Tập 2: Cho điểm O và đường thẳng ∆ không đi qua O. Gọi  d là đường thẳng đi qua O và song song với ∆. Xét hai mặt phẳng phân biệt tuỳ ý (P) và (Q) cùng chứa d. Trong các mặt phẳng (P), (Q) tương ứng kẻ các đường thẳng a, b cùng đi qua O và vuông góc với d (H.7.16). Giải thích vì sao mp(a, b) đi qua O và vuông góc với ∆.

Lời giải:

Ta có (P) = mp(d, a) và (Q) = mp(d, b).

Do (P) và (Q) là hai mặt phẳng phân biệt nên a và b là hai đường thẳng phân biệt.

Do $\left.\begin{array}{l}d\perp a\\ d\text{\hspace{0.17em}//}\Delta \end{array}\right\}\Rightarrow a\perp \Delta$ hay (D, a) = (d, a) = 90°.

Do $\left.\begin{array}{l}d\perp b\\ d\text{\hspace{0.17em}//\hspace{0.17em}}\Delta \end{array}\right\}\Rightarrow b\perp \Delta$ hay (D, b) = (d, b) = 90°.

Vậy D vuông góc với a và b và a, b đi qua O nên D ^ mp(a, b).

Giải Toán 11 trang 34 Tập 2

HĐ4 trang 34 Toán 11 Tập 2: Cho mặt phẳng (P) và điểm O. Trong mặt phẳng (P), lấy hai đường thẳng cắt nhau a, b tuỳ ý. Gọi (α), (β) là các mặt phẳng qua O và tương ứng vuông góc với a, b (H.7.19).

a) Giải thích vì sao hai mặt phẳng (α), (β) cắt nhau theo một đường thẳng ∆ đi qua O.

b) Nêu nhận xét về mối quan hệ giữa ∆ và (P).

Lời giải:

a) Vì a ^ (a) nên a và (a) có điểm chung, do đó (a) và (P) có điểm chung.

Mặt khác (a) không trùng (P) vì (a) vuông góc với a và a nằm trong (P). Do đó (a) và (P) cắt nhau theo một giao tuyến n.

Vì b ^ (b) nên b và (b) có điểm chung, do đó (b) và (P) có điểm chung.

Lại có (b) không trùng với (P) vì (b) vuông góc với b và b nằm trong (P). Do đó (b) và (P) cắt nhau theo giao tuyến m.

Do m ^ b, n ^ a và a, b cắt nhau nên m, n cắt nhau suy ra chúng phân biệt.

Do đó, (a) và (b) không thể trùng nhau. Mặt khác, (a) và (b) có điểm chung O nên chúng cắt nhau theo một đường thẳng D đi qua O.

b) Vì (a) và (b) đều đi qua O nên giao tuyến D của chúng đi qua O. Hơn nữa a, b tương ứng vuông góc với (a) và (b) nên chúng vuông góc với D. Do D vuông góc với a, b nên D vuông góc (P).

Luyện tập 2 trang 34 Toán 11 Tập 2: Cho ba điểm phân biệt A, B, C sao cho các đường thẳng AB và AC cùng vuông góc với một mặt phẳng (P). Chứng minh rằng ba điểm A, B, C thẳng hàng.

Lời giải:

Theo đề có AB ^ (P) và AC ^ (P).

Mà có duy nhất một đường thẳng đi qua A và vuông góc với (P) nên AB và AC trùng nhau. Do đó A, B, C thẳng hàng.

3. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng

HĐ5 trang 34 Toán 11 Tập 2: Cho đường thẳng a vuông góc với mặt phẳng (P) và song song với đường thẳng b. Lấy một đường thẳng m bất kì thuộc mặt phẳng (P) (H.7.20). Tính (b, m) và từ đó rút ra mối quan hệ giữa b và (P).

Lời giải:

Vì a ^ (P) mà m Ì (P) nên a ^ m hay (a, m) = 90°.

Mà b // a nên (b, m) = (a, m) = 90°.

Do b vuông góc với mọi đường thẳng m bất kì trong (P) nên b vuông góc với (P).

HĐ6 trang 34 Toán 11 Tập 2: Cho hai đường thẳng phân biệt a và b cùng vuông góc với mặt phẳng (P). Xét O là một điểm thuộc a nhưng không thuộc b. Gọi c là đường thẳng qua O và song song với b (H.7.21).

a) Hỏi c có vuông góc với với (P) hay không ? Nêu nhận xét về vị trí tương đối giữa a và c.

b) Nêu nhận xét về vị trí tương đối giữa hai đường thẳng a và b.

Lời giải:

a) Vì b ⊥ (P) và c // b nên c ⊥ (P).

Vì a và c cắt nhau tại O, mà a ⊥ (P) và c ⊥ (P) nên a và c trùng nhau.

b) Vì a và c trùng nhau và b // c nên a // b.

Giải Toán 11 trang 35 Tập 2

HĐ7 trang 35 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng ∆ vuông góc với (P). Gọi b là một đường thẳng bất kì thuộc (Q). Lấy một đường thẳng a thuộc (P) sao cho a song song với b (H.7.23). So sánh (∆, b) và (∆, a). Từ đó rút ra mối quan hệ giữa ∆ và (Q).

Lời giải:

Vì ∆ ⊥ (P) mà a thuộc (P) nên (∆, a) = 90°.

Lại có a // b nên (∆, a) = (∆, b) = 90°.

Vì (∆, b) = 90° nên ∆ ⊥ b mà b là đường thẳng bất kì thuộc (Q) nên ∆ ⊥ (Q).

HĐ8 trang 35 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng ∆. Xét O là một điểm thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q). Gọi (R) là mặt phẳng đi qua O và song song với (Q). (H.7.24).

a) Hỏi (R) có vuông góc với ∆ hay không ? Nêu nhận xét về vị trí tương đối giữa (P) và (R).

b) Nêu vị trí tương đối giữa (P) và (Q).

Lời giải:

a) Do ∆ ⊥ (Q) mà (Q) // (R) nên ∆ ⊥ (R).

Do ∆ ⊥ (R) và ∆ ⊥ (P) mà (P) và (R) cùng đi qua O nên (P) và (R) trùng nhau.

b) Vì (P) và (R) trùng nhau mà (Q) // (R) nên (P) // (Q).

Luyện tập 3 trang 35 Toán 11 Tập 2: Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn. Hỏi hai mặt phẳng đó có song song với nhau hay không ? Vì sao ?

Lời giải:

Ta coi chân bàn như đường thẳng, mặt bàn và mặt sàn là hai mặt phẳng.

Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn thì hai mặt phẳng đó song song với nhau vì hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau

HĐ9 trang 35 Toán 11 Tập 2: Cho đường thẳng a song song với mặt phẳng (P) và đường thẳng ∆ vuông góc với mặt phẳng (P). Tính (∆, a).

Lời giải:

Vì a song song với mặt phẳng (P) nên a song song với một đường thẳng b nằm trong (P).

Mà đường thẳng ∆ vuông góc với mặt phẳng (P) nên (∆, b) = 90°.

Khi đó (∆, a) = (∆, b) = 90°.

Vậy (∆, a) = 90°.

Giải Toán 11 trang 36 Tập 2

HĐ10 trang 36 Toán 11 Tập 2: Cho đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng ∆.

a) Qua một điểm O thuộc (P), kẻ đường thẳng a' song song với a. Nêu vị trí tương đối giữa a' và (P).

b) Nêu vị trí tương đối giữa a và (P).

Lời giải:

a) Do a // a' và ∆ ⊥ a nên ∆ ⊥ a'.

Lại có ∆ ⊥ (P) suy ra, a' // (P) hoặc a' thuộc (P).

Vì a' đi qua O thuộc (P) nên a' thuộc (P).

b) Vì a // a' , a' thuộc (P) nên a thuộc (P) hoặc a song song với (P).

Luyện tập 4 trang 36 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA ⊥ (ABCD). Kẻ AH vuông góc với SC (H thuộc SC), BM vuông góc với SC (M thuộc SC). Chứng minh rằng SC ⊥ (MBD) và AH // (MBD).

Lời giải:

Vì ABCD là hình vuông nên AC ⊥ BD.

Vì SA ⊥ (ABCD) nên SA ⊥ BD mà AC ⊥ BD nên BD ⊥ (SAC).

Do BD ⊥ (SAC) nên BD ⊥ SC.

Vì BM ⊥ SC mà BD ⊥ SC nên SC ⊥ (BMD).

Gọi O là giao điểm của AC và BD.

Vì SC ⊥ (BMD) nên SC ⊥ OM.

Lại có AH ⊥ SC và SC ⊥ OM nên AH // OM.

Vì AH // OM và OM $\subset$ (MBD) nên AH // (MBD).

Bài tập

Bài 7.5 trang 36 Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là tam giác cân tại A và $SA\perp \left(ABC\right)$. Gọi M là trung điểm của BC. Chứng minh rằng:

a) $BC\perp \left(SAM\right)$;

b) Tam giác SBC cân tại S.

Lời giải:

a) Vì SA ⊥ (ABC) nên SA ⊥ BC.

Vì ABC là tam giác cân tại A, AM là trung tuyến nên AM là đường cao hay AM ⊥ BC.

Do SA ⊥ BC và AM ⊥ BC nên BC ⊥ (SAM).

b) Vì BC ⊥ (SAM) nên BC ⊥ SM.

Xét tam giác SBC có SM là trung tuyến đồng thời là đường cao nên tam giác SBC cân tại S.

Bài 7.6 trang 36 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và $SA\perp \left(ABCD\right)$. Chứng minh rằng các mặt bên của hình chóp S.ABCD là các tam giác vuông.

Lời giải:

Vì SA ⊥ (ABCD) nên SA ⊥ AD, SA ⊥ AB, SA ⊥ BC, SA ⊥ CD.

Do ABCD là hình chữ nhật nên AB ⊥ BC, AD ⊥ DC.

Vì SA ⊥ AB nên tam giác SAB vuông tại A.

Vì SA ⊥ AD nên tam giác SAD vuông tại A.

Vì SA ⊥ BC và AB ⊥ BC nên BC ⊥ (SAB), suy ra BC ⊥ SB hay tam giác SBC vuông tại B.

Vì SA ⊥ CD và AD ⊥ DC nên CD ⊥ (SAD), suy ra CD ⊥ SD hay tam giác SCD vuông tại D.

Bài 7.7 trang 36 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình chữ nhật và $SA\perp \left(ABCD\right)$. Gọi M, N tương ứng là hình chiếu của A trên SB, SD. Chứng minh rằng: $AM\perp \left(SBC\right),AN\perp \left(SCD\right),SC\perp \left(AMN\right)$.

Lời giải:

- Vì SA ⊥ (ABCD) nên SA ⊥ BC.

Do ABCD là hình chữ nhật nên BC ⊥ AB mà SA ⊥ BC nên BC ⊥ (SAB), suy ra BC ⊥ AM.

Lại có, M là hình chiếu của A trên SB nên AM ⊥ SB.

Vì AM ⊥ SB và BC ⊥ AM nên AM ⊥ (SBC).

- Vì SA ⊥ (ABCD) nên SA ⊥ CD.

Do ABCD là hình chữ nhật nên AD ⊥ CD.

Vì AD ⊥ CD và SA ⊥ CD nên CD ⊥ (SAD), suy ra CD ⊥ AN.

Do N là hình chiếu của A trên SD nên AN ⊥ SD.

Vì AN ⊥ SD và CD ⊥ AN nên AN ⊥ (SCD).

- Do AM ⊥ (SBC) nên AM ⊥ SC và AN ⊥ (SCD) nên AN ⊥ SC.

Vì AM ⊥ SC và AN ⊥ SC nên SC ⊥ (AMN).

Bài 7.8 trang 36 Toán 11 Tập 2: Bạn Vinh thả quả dọi chìm vào thùng nước. Hỏi khi dây dọi căng và mặt nước yên lặng thì đường thẳng chứa dây dọi có vuông góc với mặt phẳng chứa mặt nước trong thùng hay không?

Lời giải:

Khi dây dọi căng và mặt nước yên lặng thì đường thẳng chứa dây dọi có vuông góc với mặt phẳng chứa mặt nước trong thùng.

Bài 7.9 trang 36 Toán 11 Tập 2: Một cột bóng rổ được dựng trên một sân phẳng. Bạn Hùng đo khoảng cách từ một điểm trên sân, cách chân cột 1 m đến một điểm trên cột, cách chân cột 1 m được kết quả là 1,5 m (H.7.27). Nếu phép đo của Hùng là chính xác thì cột có vuông góc với sân hay không? Có thể kết luận rằng cột không có phương thẳng đứng hay không?

Lời giải:

Có 1² + 1² ≠ 1,5² . Do đó theo định lí Pythagore thì cột không vuông góc với mặt sân.

Do đó cột không có phương thẳng đứng.

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 22: Hai đường thẳng vuông góc

Bài 23: Đường thẳng vuông góc với mặt phẳng

Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Bài 25: Hai mặt phẳng vuông góc

Bài 26: Khoảng cách

Lý thuyết Đường thẳng vuông góc với mặt phẳng

1. Đường thẳng vuông góc với mặt phẳng

Đường thẳng $\mathrm{\Delta }$ được gọi là vuông góc với mặt phẳng (P) nếu $\mathrm{\Delta }$ vuông góc với mọi đường thẳng nằm trong (P).

Chú ý: Khi $\mathrm{\Delta }$ vuông góc với (P), ta còn nói (P) vuông góc với $\mathrm{\Delta }$ hoặc $\mathrm{\Delta }$ và (P) vuông góc với nhau, kí hiệu $\mathrm{\Delta }\mathrm{\perp }\left(P\right)$.

2. Điều kiện để đường thẳng vuông góc với mặt phẳng

Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.

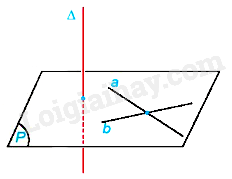
3. Tính chất

- Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

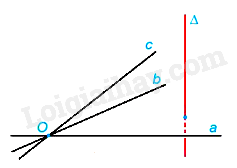
Nhận xét: Nếu ba đường thẳng đôi một phân biệt a, b, c cùng đi qua một điểm O và cùng vuông góc với một đường thẳng $\mathrm{\Delta }$ thì ba đường thẳng đó cùng nằm trong mặt phẳng đi qua O và vuông góc với $\mathrm{\Delta }$.

Chú ý: Mặt phẳng đi qua trung điểm của đoạn thẳng AB và vuông góc với đường thẳng AB được gọi là mặt phẳng trung trực của đoạn thẳng AB. Mặt phẳng trung trực của đoạn thẳng AB là tập hợp các điểm cách đều hai điểm A, B.

- Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng

- Nếu đường thẳng a vuông góc với mặt phẳng (P) và mặt phẳng (P) song song với mặt phẳng (Q) thì a vuông góc với (Q).

- Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

- Nếu đường thẳng $\mathrm{\Delta }$ vuông góc với mặt phẳng (P) thì $\mathrm{\Delta }$ cũng vuông góc với các mặt phẳng song song với (P).

- Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

- Nếu đường thẳng $\mathrm{\Delta }$ vuông góc với mặt phẳng (P) thì $\mathrm{\Delta }$ vuông góc với mọi đường thẳng song song với (P).

- Nếu đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng $\mathrm{\Delta }$ thì a nằm trong (P) hoặc song song với (P).