Với lời giải SBT Toán 10 trang 50 Tập 1 chi tiết trong Bài 8: Tổng và hiệu của hai vectơ sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 8: Tổng và hiệu của hai vectơ

Bài 4.7 trang 50 SBT Toán 10 Tập 1:

Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ không cùng phương. Chứng minh rằng:

$\left|\overrightarrow{a}\right|-\left|\overrightarrow{b}\right|<\left|\overrightarrow{a}+\overrightarrow{b}\right|<\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|$

Lời giải:

Giả sử ba điểm A, B, C thoả mãn: $\overrightarrow{a}=\overrightarrow{AB},\overrightarrow{b}=\overrightarrow{BC}$ 

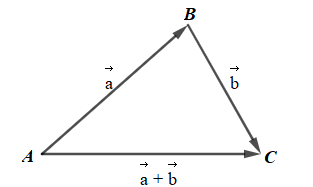
Khi đó ta có: $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ (quy tắc ba điểm)

Do đó:

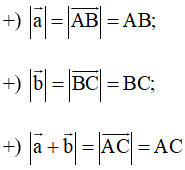
Mặt khác: xét tam giác ABC, theo bất đẳng thức trong tam giác ta có:

AB – BC < AC < AB + BC

Hay $\left|\overrightarrow{a}\right|-\left|\overrightarrow{b}\right|<\left|\overrightarrow{a}+\overrightarrow{b}\right|<\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|$ 

Vậy $\left|\overrightarrow{a}\right|-\left|\overrightarrow{b}\right|<\left|\overrightarrow{a}+\overrightarrow{b}\right|<\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|.$

Bài 4.8 trang 50 SBT Toán 10 Tập 1:

Cho hình bình hành ABCD tâm O. M là một điểm tuỳ ý thuộc cạnh BC, khác B và C. MO cắt cạnh AD tại N.

a) Chứng minh rằng O là trung điểm MN.

b) Gọi G là trọng tâm tam giác BCD. Chứng minh rằng G cũng là trọng tâm tam giác MNC.

Lời giải:

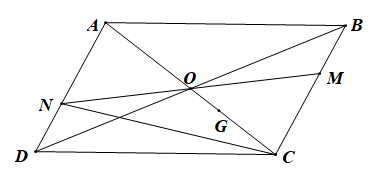
a) Vì ABCD là hình bình hành tâm O

Nên O là trung điểm của AC và BD và $\widehat{ADO}=\widehat{CBO}$ 

Xét ∆ODN và ∆OBM có:

OD = OB (do O là trung điểm của BD),

$\widehat{DON}=\widehat{BOM}$ (hai góc đối đỉnh),

$\widehat{NDO}=\widehat{MBO}$(do $\widehat{ADO}=\widehat{CBO}$)

Þ ∆ODN = ∆OBM (g.c.g)

Þ ON = OM (hai cạnh tương ứng)

Þ O là trung điểm của NM.

Vậy O là trung điểm của NM.

b) Vì G là trọng tâm ∆BCD nên $\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$ 

$\Rightarrow \left(\overrightarrow{GM}+\overrightarrow{MB}\right)+\overrightarrow{GC}+\left(\overrightarrow{GN}+\overrightarrow{ND}\right)=\overrightarrow{0}$ (quy tắc hiệu)

$\Rightarrow \overrightarrow{GM}+\overrightarrow{MB}+\overrightarrow{GC}+\overrightarrow{GN}+\overrightarrow{ND}=\overrightarrow{0}$

$\Rightarrow \overrightarrow{GM}+\overrightarrow{GC}+\overrightarrow{GN}+\left(\overrightarrow{MB}+\overrightarrow{ND}\right)=\overrightarrow{0}$ (*)

Ta có: O là trung điểm của NM (câu a), O là trung điểm của BD (câu a)

Þ BMDN là hình bình hành

$\Rightarrow \overrightarrow{BM}=\overrightarrow{ND}$ $\Rightarrow -\overrightarrow{MB}=\overrightarrow{ND}$ 

$\Rightarrow \overrightarrow{MB}+\overrightarrow{ND}=\overrightarrow{0}$ 

Thay vào (*) ta được $\overrightarrow{GM}+\overrightarrow{GC}+\overrightarrow{GN}+\overrightarrow{0}=\overrightarrow{0}$

Do đó $\overrightarrow{GM}+\overrightarrow{GC}+\overrightarrow{GN}=\overrightarrow{0}$

Þ G là trọng tâm tam giác MNC.

Vậy G là trọng tâm tam giác MNC.

Bài 4.9 trang 50 SBT Toán 10 Tập 1:

Cho tứ giác ABCD.

a) Chứng minh rằng $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{0}$ 

b) Chứng minh rằng $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}.$ 

Lời giải:

a) Theo quy tắc ba điểm ta có:

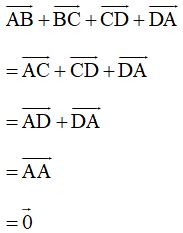
 Vậy $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{0}$

b) Theo quy tắc ba điểm ta có:

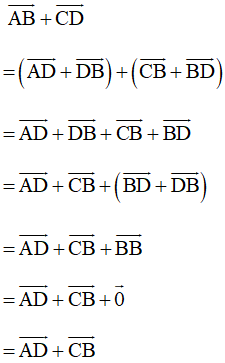
Vậy $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}.$

Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:

Giải SBT Toán 10 trang 51 Tập 1

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 7: Các khái niệm mở đầu

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vectơ với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ