Với lời giải SBT Toán 10 trang 40 Tập 1 chi tiết trong Bài tập cuối chương 3 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài tập cuối chương 3
Bài 3.17 trang 40 SBT Toán 10 Tập 1:
Tam giác ABC có Giá trị của tanC bằng
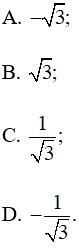
Lời giải:
Đáp án đúng là: A
Xét tam giác ABC ta có:
Do đó tanC = tan120° =
Ta chọn phương án A.
Bài 3.18 trang 40 SBT Toán 10 Tập 1:
Trên mặt phẳng toạ độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho Tích hoành độ và tung độ của điểm M bằng
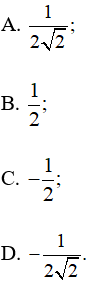
Lời giải:
Đáp án đúng là: C
Ta có
và
Mà xM = và yM =
Do đó xM.yM =
Ta chọn phương án C.
Bài 3.19 trang 40 SBT Toán 10 Tập 1:
Trên mặt phẳng toạ độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho N là điểm đối xứng với M qua trục tung. Giá trị của tan bằng
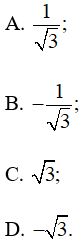
Lời giải:
Đáp án đúng là: A
Vì N đối xứng với M qua trục tung nên ta có:
• xN = –xM
Þ cos = –cos
Þ cos = –cos150°
Þ cos =
• yN = yM
sin = sin
sin = sin150°
sin =
• Ta có: tan =
Ta chọn phương án A.
Bài 3.20 trang 40 SBT Toán 10 Tập 1:
Cho góc nhọn α có tanα = Giá trị của tích sinα.cosα bằng
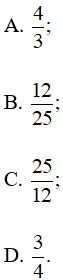
Lời giải:
Đáp án đúng là: B
Ta có: tanα =
Do đó sinα.cosα = cosα.cosα = cos2α.
Mặt khác tanα =
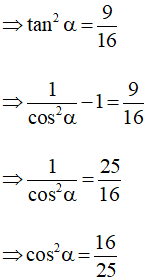
Do đó sinα.cosα =
Ta chọn phương án B.
Bài 3.21 trang 40 SBT Toán 10 Tập 1:
Cho góc α (0° < α < 180°) thõa mãn sinα + cosα = 1. Giá trị của cotα là
A. 0;
B. 1;
C. –1;
D. Không tồn tại.
Lời giải:
Đáp án đúng là: A
Ta có: sinα + cosα = 1.
(sinα + cosα)2 = 12.
sin2α + 2.sinα.cosα + cos2α = 1.
(sin2α + cos2α) + 2.sinα.cosα = 1.
1 + 2.sinα.cosα = 1.
2.sinα.cosα = 0.
sinα.cosα = 0.
cosα = 0
(Vì 0° < α < 180° nên sinα > 0)
cotα =
Ta chọn phương án A.
Bài 3.22 trang 40 SBT Toán 10 Tập 1:
Cho góc α thỏa mãn sinα + cosα = Giá trị của tanα + cotα là
A. 1;
B. –2;
C. 0;
D. 2.
Lời giải:
Đáp án đúng là: D
Ta có: sinα + cosα =
(sinα + cosα)2 = 2
sin2α + 2.sinα.cosα + cos2α = 2
(sin2α + cos2α) + 2.sinα.cosα = 2
1 + 2.sinα.cosα = 2
2.sinα.cosα = 1
sinα.cosα =
tanα + cotα =
Ta chọn phương án D.
Bài 3.23 trang 40 SBT Toán 10 Tập 1:
Trên mặt phẳng toạ độ Oxy lấy M thuộc nửa đường tròn đơn vị, sao cho (H.3.4).
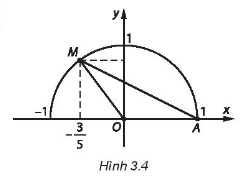
Diện tích của tam giác AOM bằng
Lời giải:
Đáp án đúng là: B
Gọi h là độ dài đường cao kẻ từ M đến OA của tam giác OAM.
Khi đó h = yM = sin
Mà sin2 + cos2 = 1
sin2 = 1 –
sin2 =
sin2 =
Mà Þ sin > 0
Do đó sin =
Ta có:
Ta chọn phương án B.
Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:
Giải SBT Toán 10 trang 41 Tập 1
Giải SBT Toán 10 trang 42 Tập 1
Giải SBT Toán 10 trang 43 Tập 1
Giải SBT Toán 10 trang 44 Tập 1
Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 6: Hệ thức lượng trong tam giác
Bài 8: Tổng và hiệu của hai vectơ
Bài 9: Tích của một vectơ với một số