Với giải Bài 10 trang 11 SBT Toán lớp 8 Chân trời sáng tạo chi tiết trong Bài 2: Các phép toán với đa thức nhiều biến giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 2: Các phép toán với đa thức nhiều biến
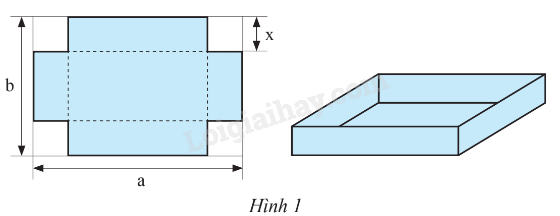
Bài 10 trang 11 SBT Toán 8 Tập 1: Từ một tấm tôn hình chữ nhật có chiều dài bằng a (cm), chiều rộng bằng b (cm), người ta cắt bỏ bốn hình vuông cạnh bằng x (cm) ở bốn góc, rồi gấp và hàn thành thùng không có nắp (Hình 1). Viết biểu thức biểu thị:
a) Thể tích nước tối đa mà thùng có thể chứa được.
b) Tổng diện tích của năm mặt của chiếc thùng.
Lời giải:
Thùng trên có chiều dài là: , chiều rộng là , chiều cao là x (cm)
a) Thể tích của thùng là:
Vậy thể tích nước tối đa mà thùng có thể chứa được là
b) Tổng diện tích năm mặt của chiếc thùng là:
Vậy tổng diện tích của năm mặt của chiếc thùng là
Xem thêm lời giải sách bài tập Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 10 SBT Toán 8 Tập 1: Tính:...
Bài 2 trang 10 SBT Toán 8 Tập 1: Tính:....
Bài 3 trang 10 SBT Toán 8 Tập 1: Thực hiện các phép nhân:...
Bài 4 trang 10 SBT Toán 8 Tập 1: Thực hiện các phép nhân:....
Bài 5 trang 10 SBT Toán 8 Tập 1: Thực hiện các phép chia:...
Bài 6 trang 10 SBT Toán 8 Tập 1: Thực hiện các phép chia:....
Bài 7 trang 10 SBT Toán 8 Tập 1: Tính:...
Bài 8 trang 10 SBT Toán 8 Tập 1: Tính giá trị của đa thức:...
Bài 9 trang 11 SBT Toán 8 Tập 1: Biết rằng và . Tính các đa thức sau theo a và b......
Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Đơn thức và đa thức nhiều biến
Bài 2: Các phép toán với đa thức nhiều biến
Bài 3: Hằng đẳng thức đáng nhớ
Bài 4: Phân tích đa thức thành nhân tử
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
