Cho tam giác ABC vuông cân tại A có độ dài cạnh góc vuông AB và AC là 4 cm

Cho tam giác ABC vuông cân tại A có độ dài cạnh góc vuông AB và AC là 4 cm

Van Anh Ngày: 05-09-2023 Lớp 8

1.4 K

Với giải Bài 4 trang 88 SBT Toán lớp 8 Cánh diều chi tiết trong Bài 1: Định lí Pythagore giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 1: Định lí Pythagore

Bài 4 trang 88 SBT Toán 8 Tập 1: Cho tam giác $A B C$ vuông cân tại $A$ có độ dài cạnh góc vuông $A B$ và $A C$ là 4 cm. Kẻ đường cao $A D$ của tam giác $A B C$ .

a) Tính độ dài cạnh đáy $B C$ (làm tròn kết quả đến hàng phần trăm của centimet)

b) Tính độ dài đường cao $A D$ (làm tròn kết quả đến hàng phần trăm của centimet)

Lời giải:

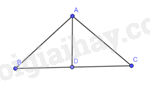
Sách bài tập Toán 8 Bài 1 (Cánh diều): Định lí Pythagore (ảnh 5)

a) Áp dụng định lí Pythagore ta có:

$B C^{2} = A B^{2} + A C^{2} = 32$

Suy ra $B C = \sqrt{32} \approx 5, 66 (c m)$

b) Lại có $Δ A B D = Δ A C D$ (cạnh huyền-cạnh góc vuông)

Suy ra $B D = C D$ . Vậy $D$ là trung điểm của $B C$ .

Do đó $C D = \frac{B C}{2} = \frac{\sqrt{32}}{2} \approx 2, 83 (c m)$

Tam giác $A C D$ vuông tại $D$ nên ta tính được $A D \approx 2, 83 (c m)$ .

Xem thêm lời giải sách bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 1 trang 87 SBT Toán 8 Tập 1: Tính độ dài $x, y, z$ ở các hình $3 a, 3 b, 3 c, 3 d$ (độ dài ở các hình là cùng đơn vị đo):....

Bài 2 trang 88 SBT Toán 8 Tập 1: Hình 4 mô tả một chiếc thước của người thợ sử dụng khi xây móng nhà để kiểm tra xem hai phần móng nhà có vuông góc với nhau hay không . Trên hình, ta đo được $A B = 4 d m$ , $A C = 3 d m$ và $B C = 5 d m$ . Em hãy giải thích vì sao hai cạnh của chiếc thước đó vuông góc với nhau.....

Bài 3 trang 88 SBT Toán 8 Tập 1: Tính chu vi của tứ giác $A B C D$ ở Hình 5 (làm tròn kết quả đến hàng phần trăm của centimet). Biết rằng độ dài cạnh mỗi ô vuông là 1 cm....

Bài 4 trang 88 SBT Toán 8 Tập 1: Cho tam giác $A B C$ vuông cân tại $A$ có độ dài cạnh góc vuông $A B$ và $A C$ là 4 cm. Kẻ đường cao $A D$ của tam giác $A B C$ .....

Bài 5 trang 88 SBT Toán 8 Tập 1: Cho tam giác $A B C$ vuông cân tại $A$ . Qua $A$ kẻ đường thẳng $d$ bất kì sao cho đường thẳng $d$ không cắt đoạn thẳng $B C$ . Gọi $D, E$ lần lượt là hình chiếu của $B, C$ trên đường thẳng $d$ . Chứng minh $A D^{2} + A E^{2}$ không phụ thuộc vào vị trí của đường thẳng $d$ .....

Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 4

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

284

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

236

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

187

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

193

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.