Với giải sách bài tập Toán 10 Bài 1: Mệnh đề toán học sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 1: Mệnh đề toán học

Giải SBT Toán 10 trang 7

Bài 1 trang 7 SBT Toán 10 Tập 1: Cho mệnh đề A: “Nghiệm của phương trình x² – 5 = 0 là số hữu tỉ”. Mệnh đề phủ định của mệnh đề trên là:

A. “Nghiệm của phương trình x² – 5 = 0 không là số hữu tỉ”.

B. “Nghiệm của phương trình x² – 5 = 0 không là số vô tỉ”.

C. “Phương trình x² – 5 = 0 vô nghiệm”.

D. “Nghiệm của phương trình x² – 5 = 0 không là số nguyên”.

Lời giải

Đáp án đúng là A

Mệnh đề phủ định của mệnh đề A là $\overline{A}$: “Nghiệm của phương trình x² – 5 = 0 không là số hữu tỉ”.

Bài 2 trang 7 SBT Toán 10 Tập 1: Cho số tự nhiên n. Xét mệnh đề: “Nếu số tự nhiên n chia hết cho 4 thì n chia hết cho 2”. Mệnh đề đảo của mệnh đề đó là:

A. “Nếu số tự nhiên n chia hết cho 2 thì n không chia hết cho 4”.

B. “Nếu số tự nhiên n chia hết cho 4 thì n không chia hết cho 2”.

C. “Nếu số tự nhiên n chia hết cho 2 thì n chia hết cho 4”.

D. “Nếu số tự nhiên n không chia hết cho 2 thì n không chia hết cho 4”.

Lời giải

Đáp án đúng là C

Mệnh đề đảo của mệnh đề đã cho là “Nếu số tự nhiên n chia hết cho 2 thì n chia hết cho 4”.

Bài 3 trang 7 SBT Toán 10 Tập 1: Cho tứ giác ABCD. Xét mệnh đề “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau”. Mệnh đề đảo của mệnh đề đó là:

A. “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD không có hai đường chéo bằng nhau”.

B. “Nếu tứ giác ABCD không có hai đường chéo bằng nhau thì tứ giác ABCD không là hình chữ nhật”.

C. “Nếu tứ giác ABCD không có hai đường chéo bằng nhau thì tứ giác ABCD không là hình chữ nhật”.

D. “Nếu tứ giác ABCD có hai đường chéo bằng nhau thì tứ giác ABCD là hình chữ nhật”.

Lời giải

Đáp án đúng là D

Mệnh đề đảo của mệnh đề của mệnh đề đã cho là: “Nếu tứ giác ABCD có hai đường chéo bằng nhau thì tứ giác ABCD là hình chữ nhật”.

Giải SBT Toán 10 trang 8

Bài 4 trang 8 SBT Toán 10 Tập 1: Phủ định của mệnh đề “∃x ∈ ℝ, x² – x + 1 < 0” là mệnh đề:

A. “∀x ∈ ℝ, x² – x + 1 ≥ 0”.

B. “∀x ∈ ℝ, x² – x + 1 < 0”.

C. “∀x ∈ ℝ, x² – x + 1 > 0”.

D. “∃x ∈ ℝ, x² – x + 1 ≥ 0”.

Lời giải

Đáp án đúng là A

Phủ định của mệnh đề “∃x ∈ ℝ, x² – x + 1 < 0” là mệnh đề “∀x ∈ ℝ, x² – x + 1 ≥ 0”.

Bài 5 trang 8 SBT Toán 10 Tập 1: Phủ định của mệnh đề “∃x ∈ ℚ, x = $\frac{1}{x}$” là mệnh đề:

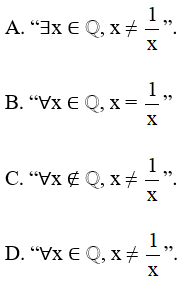
Lời giải

Đáp án đúng là D

Phủ định của mệnh đề “∃x ∈ ℚ, x = $\frac{1}{x}$” là mệnh đề: “∀x ∈ ℚ, x ≠ $\frac{1}{x}$”.

Bài 6 trang 8 SBT Toán 10 Tập 1: Phủ định của mệnh đề “∀x ∈ ℝ, x² ≥ 0” là mệnh đề:

A. “∃x ∈ ℝ, x² ≥ 0”.

B. “∃x ∈ ℝ, x² > 0”.

C. “∃x ∈ ℝ, x² ≤ 0”.

D. “∃x ∈ ℝ, x² < 0”.

Lời giải

Đáp án đúng là D

Phủ định của mệnh đề “∀x ∈ ℝ, x² ≥ 0” là mệnh đề: “∃x ∈ ℝ, x² < 0”.

Bài 7 trang 8 SBT Toán 10 Tập 1: Phủ định của mệnh đề “∀x ∈ ℝ, |x| ≥ x” là mệnh đề:

A. “∀x ∈ ℝ, |x| < x”

B. “∃x ∈ ℝ, |x| ≤ x”.

C. “∃x ∈ ℝ, |x| < x”.

D. “∃x ∈ ℝ, |x| > x”.

Lời giải

Đáp án đúng là C

Phủ định của mệnh đề “∀x ∈ ℝ, |x| ≥ x” là mệnh đề: “∃x ∈ ℝ, |x| < x”.

Bài 8 trang 8 SBT Toán 10 Tập 1: Cho x, y là hai số thực cùng khác  – 1. Kết luận nào sau đây là đúng?

A. x + y + xy ≠ – 1.

B. x + y + xy = – 1.

C. x + y ≠ – 2.

D. xy ≠ – 1.

Lời giải

Đáp án đúng là A

Ta có x ≠ – 1 ⇔ x + 1 ≠ 0 và y ≠ – 1 ⇔ y + 1 ≠ 0

⇒ (x + 1)(y + 1) ≠ 0

⇔ xy + x + y + 1 ≠ 0

⇔ xy + x + y ≠ – 1.

Bài 9 trang 8 SBT Toán 10 Tập 1: Cho a, b là hai số thực thỏa mãn a + b < 2. Kết luận nào sau đây là đúng?

A. Cả hai số a, b đều nhỏ hơn 1.

B. Có ít nhất một trong hai số a, b nhỏ hơn 1.

C Có ít nhất một trong hai số a, b lớn hơn 1.

D. Cả hai số a, b không vượt quá 1.

Lời giải

Đáp án đúng là B.

Ta có: a + b < 2

+) Nếu a = 2 > 1 và b = – 2 thì a + b = 2 + (– 2) = 0 < 2.

Do đó không nhất thiết cả hai số a và b đều nhỏ hơn 1 thì a + b < 2. Suy ra A sai.

+)  Chọn a = 3 > 1 và b = 0 thì a + b = 3 + 1 = 3 > 2. Suy ra không thỏa mãn. Do đó C sai.

+) Chọn a = 1, b = 1 thì a + b = 2. Suy ra không thỏa mãn. Do đó D sai.

Bài 10 trang 8 SBT Toán 10 Tập 1: Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?

a) Số π là số vô tỉ;

b) Bình phương của mọi số thực đều là số dương;

c) Tồn tại số thực x mà x lớn hơn số nghịch đảo của nó;

d) Fansipan là ngọn núi cao nhất Việt Nam.

Lời giải

Mệnh đề toán học là những khẳng định liên quan đến những vấn đề trong toán học.

Và trong các phát biểu đã cho, ta thấy có phát biểu a), b), c) là các khẳng định liên quan đến vấn đề trong toán học. Do đó a), b), c) là mệnh đề toán học.

Giải SBT Toán 10 trang 9

Bài 11 trang 9 SBT Toán 10 Tập 1: Nêu mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mỗi mệnh đề phủ định đó:

a) A: “Trục đối xứng của đồ thị hàm số y = – x² là trục tung”;

b) B: “Phương trình 3x² + 1 có nghiệm”;

c) C: “Hai đường thẳng y = 2x + 1 và y = – 2x + 1 không song song với nhau”;

d) D: “Số 2 024 không chia hết cho 4”.

Lời giải

a) Mệnh đề phủ định của mệnh đề A: “Trục đối xứng của đồ thị hàm số y = – x² là trục tung” là $\overline{A}$: “Trục đối xứng của đồ thị hàm số y = – x² không phải là trục tung”.

Hàm số y = – x² có trục đối xứng là trục tung. Do đó mệnh đề A đúng, mệnh đề $\overline{A}$ sai.

b) Mệnh đề phủ định của mệnh đề B: “Phương trình 3x² + 1 có nghiệm” là $\overline{B}$: “Phương trình 3x² + 1 vô nghiệm”.

Xét phương trình 3x²  + 1 = 0

⇔ 3x² = – 1 (vô lí)

Suy ra phương trình đã cho vô nghiệm.

Do đó mệnh đề B sai, mệnh đề $\overline{B}$ đúng.

c) Mệnh đề phủ định của mệnh đề C: “không song song với nhau” là mệnh đề $\overline{C}$: “Hai đường thẳng y = 2x + 1 và y = – 2x + 1 song song với nhau”.

Ta có y = 2x + 1 có a = 2, b = 1

y = – 2x + 1 có a’ = – 2, b’ = 1

Suy ra a ≠ a’ nên hai đường thẳng y = 2x + 1 và y = – 2x + 1 cắt nhau. Do đó mệnh đề C đúng và mệnh đề $\overline{C}$ sai.

d) Mệnh đề phủ định của mệnh đề D: “Số 2 024 không chia hết cho 4” là mệnh đề $\overline{D}$: “Số 2 024 chia hết cho 4”.

Ta có: 2 024 : 4 = 506 nên 2 024 chia hết cho 4. Do đó mệnh đề D sai, mệnh đề $\overline{D}$ đúng.

Bài 12 trang 9 SBT Toán 10 Tập 1: Cho mệnh đề kéo theo có dạng P ⇒ Q: “Vì 120 chia hết cho 6 nên 120 chia hết cho 9”.

a) Mệnh đề trên đúng hay sai?

b) Phát biểu mệnh đề đảo của mệnh đề trên và xét tính đúng sai của mệnh đề đảo đó.

Lời giải

a) Xét mệnh đề kéo theo P ⇒ Q: “Vì 120 chia hết cho 6 nên 120 chia hết cho 9”.

Khi đó P: “120 chia hết cho 6”; Q: “120 chia hết cho 9”.

Ta có 120 : 6 = 20 nên 120 chia hết cho 6 suy ra mệnh đề P đúng.

120 : 9 = 13 (dư 3) nên 120 không chia hết cho 9 suy ra mệnh đề Q sai.

Do đó mệnh đề P ⇒ Q là mệnh đề sai.

b) Mệnh đề đảo của mệnh đề trên được phát biểu như sau:

Q ⇒ P: “Vì 120 chia hết cho 9 nên 120 chia hết cho 6”.

Do đó mệnh đề Q ⇒ P là mệnh đề đúng.

Bài 13 trang 9 SBT Toán 10 Tập 1: Cho mệnh đề kéo theo có dạng P ⇒ Q: “Nếu tứ giác ABCD là hình bình hành thì tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường”

a) Mệnh đề trên đúng hay sai?

b) Phát biểu mệnh đề đảo của mệnh đề trên và xét tính đúng sai của mệnh đề đảo đó.

Lời giải

a) Ta có tứ giác ABCD là hình bình hành nên ABCD có tính chất là hai đường chéo cắt nhau tại trung điểm mỗi đường.

Do đó mệnh đề P ⇒ Q là mệnh đề đúng.

b) Mệnh đề đảo của mệnh đề trên là Q ⇒ P: “Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành”

Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên tứ giác ABCD là hình bình hành. Do đó mệnh đề Q ⇒ P là đúng.

Bài 14 trang 9 SBT Toán 10 Tập 1: Cho tam giác ABC với đường trung tuyến AM. Xét các mệnh đề sau:

P: “Tam giác ABC vuông tại A”.

Q: “Độ dài đường trung tuyến AM bằng nửa độ dài cạnh BC”.

a) Phát biểu mệnh đề P ⇒ Q, Q ⇒ P và xác định tính đúng sai của mỗi mệnh đề đó.

b) Nếu cả hai mệnh đề trong ý a) là đúng, hãy phát biểu mệnh đề tương đương.

Lời giải

a) +) Mệnh đề P ⇒ Q được phát biểu như sau:

“Nếu tam giác ABC vuông tại A thì độ dài đường trung tuyến AM bằng nửa độ dài cạnh BC”.

Xét tam giác ABC vuông tại A có AM là đường trung tuyến thì AM = $\frac{1}{2}$BC. Do đó mệnh đề P ⇒ Q  là mệnh đề đúng.

+) Mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu độ dài đường trung tuyến AM bằng nửa độ dài cạnh BC thì tam giác ABC vuông tại A”.

Xét tam giác ABC có đường trung tuyến AM = $\frac{1}{2}$BC.

⇒ AM = MB = MC

⇒ ∆AMB cân tại M

⇒ $\widehat{MAB}=\widehat{MBA}$ hay $\widehat{MAB}=\widehat{CBA}$

Tương tự ta có ∆AMC cân tại M

⇒ $\widehat{MAC}=\widehat{MCA}$ hay $\widehat{MAC}=\widehat{BCA}$

Mà $\widehat{MAB}+\widehat{MAC}=\widehat{BAC}$ nên $\widehat{BAC}=\widehat{BCA}+\widehat{CBA}$

Ta lại có: $\widehat{BAC}+\widehat{BCA}+\widehat{CBA}=180°$

⇒ $\widehat{BAC}=\widehat{BCA}+\widehat{CBA}=90°$

⇒ ∆ABC vuông tại A.

Do đó mệnh đề Q ⇒ P là mệnh đề đúng.

b) Vì mệnh đề P ⇒ Q và Q ⇒ P là các mệnh đề đúng nên ta có mệnh đề tương đương P ⇔ Q và được phát biểu như sau:

“Tam giác ABC vuông tại A tương đương độ dài đường trung tuyến AM bằng nửa độ dài cạnh BC”.

Bài 15 trang 9 SBT Toán 10 Tập 1: Dùng kí hiệu ∀ hoặc ∃ để viết các mệnh đề sau:

a) Có một số nguyên không chia hết cho chính nó.

b) Có một số thực mà bình phương của nó cộng với 1 bằng 0.

c) Mọi số nguyên dương đều lớn hơn nghịch đảo của nó.

d) Mọi số thực đều lớn hơn số đối của nó.

Lời giải

a) Bằng kí hiệu ∃ ta viết mệnh đề đã cho dưới dạng kí hiệu là:

“∃ x ∈ ℕ, x không chia hết cho x”.

b) Bằng kí hiệu ∃ ta viết mệnh đề đã cho dưới dạng kí hiệu là:

“∃ x ∈ ℝ, x² + 1 = 0”.

c) Bằng kí hiệu ∀ ta viết mệnh đề đã cho dưới dạng kí hiệu là:

 “∀x ∈ ℤ, x > 0 và x > $\frac{1}{x}$”.

d) Bằng kí hiệu ∀ ta viết mệnh đề đã cho dưới dạng kí hiệu là:

  “∀x ∈ ℤ, x > – x ”.

Bài 16 trang 9 SBT Toán 10 Tập 1: Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mỗi mệnh đề phủ định đó.

a) ∀n ∈ ℕ, n(n + 1) chia hết cho 2;

b) ∀x ∈ ℝ, x² > x;

c) ∃x ∈ ℝ, |x| > x;

d) ∃x ∈ ℚ, x² – x – 1 = 0.

Lời giải

a) Gọi A: “∀n ∈ ℕ, n(n + 1) chia hết cho 2”

Mệnh đề phủ định của mệnh đề A: “∀n ∈ ℕ, n(n + 1) chia hết cho 2” là $\overline{A}$: “∃n ∈ ℕ, n(n + 1) không chia hết cho 2”.

+) Xét tính đúng sai:

Với n = 2k (k ∈ ℕ) khi đó  n.(n + 1) = 2k.(2k + 1) chia hết cho 2.

Với n = 2k + 1 (k ∈ ℕ) khi đó  n.(n + 1) = (2k + 1).(2k + 2) = (2k + 1)(k + 1).2 chia hết cho 2.

Suy ra với mọi giá trị của n thì n(n + 1) chia hết cho 2. Do đó mệnh đề A đúng và $\overline{A}$ sai.

b) Gọi B: “∀x ∈ ℝ, x² > x”

Mệnh đề phủ định của mệnh đề B: “∀x ∈ ℝ, x² > x” là $\overline{B}$: “∃x ∈ ℝ, x² ≤ x”.

Xét x² > x

⇔ x² – x > 0

⇔ x(x – 1) > 0

⇔ $\left[\begin{array}{l}\left\{\begin{array}{l}x>0\\ x-1>0\end{array}\right.\\ \left\{\begin{array}{l}x<0\\ x-1<0\end{array}\right.\end{array}\right.\iff \left[\begin{array}{l}x>1\\ x<0\end{array}\right.$

Suy ra không phải với mọi số thực x thì x² > x.

Do đó mệnh đề B sai, mệnh đề $\overline{B}$ đúng.

c) Gọi C: “∃x ∈ ℝ, |x| > x”.

Mệnh đề phủ định của mệnh đề C: “∃x ∈ ℝ, |x| > x” là mệnh đề $\overline{C}$: “∀x ∈ ℝ, |x| ≤ x”.

Ta luôn có |x| ≥ x với mọi giá trị thực của x. Do đó mệnh đề C là mệnh đề đúng, mệnh đề $\overline{C}$ là mệnh đề sai.

d) Gọi D: “∃x ∈ ℚ, x² – x – 1 = 0”

Mệnh đề phủ định của mệnh đề C: “∃x ∈ ℚ, x² – x – 1 = 0” là mệnh đề $\overline{D}$: “∀x ∈ ℚ, x² – x – 1 ≠ 0”.

Xét phương trình x² – x – 1 = 0

Có: ∆ = (-1)² – 4.1.(-1) = 1 + 4 = 5 > 0

Khi đó phương trình có hai nghiệm $x_1=\frac{1+\sqrt{5}}{2}$ và $x_2=\frac{1-\sqrt{5}}{2}$.

Mà $\frac{1+\sqrt{5}}{2};\frac{1-\sqrt{5}}{2}\notin \mathbb{Q}$

Do đó không tồn tại số hữu tỉ x nào để x² – x – 1 = 0.

Vì vậy mệnh đề C sai và mệnh đề $\overline{D}$ đúng.

Giải SBT Toán 10 trang 10

Bài 17 trang 10 SBT Toán 10 Tập 1: Cho phương trình ax² + bx + c = 0.

a) Xét mệnh đề “Nếu a + b + c = 0 thì phương trình ax² + bx + c = 0 có một nghiệm bằng 1”. Mệnh đề này đúng hay sai?

b) Phát biểu mệnh đề đảo của mệnh đề trên. Mệnh đề đảo đúng hay sai?

c) Nêu điều kiện cần và đủ để phương trình ax² + bx + c = 0 có một nghiệm bằng 1.

Lời giải

a) Ta có a + b + c = 0 cần chứng minh phương trình ax² + bx + c = 0 có một nghiệm bằng 1, thật vậy:

Thay x = 1 vào phương trình ax² + bx + c = 0, ta được:

a.1² + b.1 + c = 0

⇔ a + b + c = 0 (luôn đúng).

Do đó mệnh đề “Nếu a + b + c = 0 thì phương trình ax² + bx + c = 0 có một nghiệm bằng 1” là mệnh đề đúng.

b) Mệnh đề đảo của mệnh đề trên được phát biểu như sau:

“ Nếu phương trình ax² + bx + c = 0 có một nghiệm bằng 1 thì a + b + c = 0”

Vì x = 1 là nghiệm của phương trình đã cho nên ta có: a.1² + b.1 + c = 0 ⇔ a + b + c = 0. Do đó mệnh đề đảo là mệnh đề đúng. 

c) Ta có mệnh đề “Nếu a + b + c = 0 thì phương trình ax² + bx + c = 0 có một nghiệm bằng 1” là mệnh đề đúng và mệnh đề đảo “ Nếu phương trình ax² + bx + c = 0 có một nghiệm bằng 1 thì a + b + c = 0” là mệnh đề đúng. Do đó ta có “Điều kiện cần và đủ để phương trình ax² + bx + c = 0 có một nghiệm bằng 1 là a + b + c = 0”.

Bài giảng Toán 10 Bài 1: Mệnh đề toán học - Cánh diều

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

Bài 2: Tập hợp. Các phép toán trên tập hợp

Bài ôn tập chương 1

Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Lý thuyết Mệnh đề toán học

1. Mệnh đề toán học

• Mệnh đề toán học là mệnh đề khẳng định một sự kiện trong toán học.

Ví dụ:

+ “Hà Nội là thủ đô của Việt Nam” không phải một sự kiện toán học. Do đó khẳng định này không phải mệnh đề toán học.

+ “Số π là một số hữu tỉ” là khẳng định một sự kiện trong toán học. Do đó khẳng định này là một mệnh đề toán học.

• Mỗi mệnh đề toán học phải đúng hoặc sai, không thể vừa đúng, vừa sai.

- Khi mệnh đề toán học là đúng, ta gọi mệnh đề đó là một mệnh đề đúng.

- Khi mệnh đề toán học là sai, ta gọi mệnh đề đó là một mệnh đề sai.

Ví dụ:

+ “Tổng ba góc trong tam giác bằng 180⁰” là một mệnh đề đúng.

+ “$\sqrt{2}$ là số hữu tỉ” là một mệnh đề sai (vì $\sqrt{2}\approx 1,\mathrm{414213562...}$là một số vô tỉ).

2. Mệnh đề chứa biến

• Ở mệnh đề chứa biến, ta chưa thể khẳng định ngay tính đúng hoặc sai. Với mỗi giá trị cụ thể của biến số, ta có một mệnh đề toán học mà ta có thể khẳng định tính đúng hoặc sai của mệnh đề.

Kí hiệu mệnh đề chứa biến n là P(n), mệnh đề chứa biến x, y là P(x, y), …

Ví dụ:

+ P(x): “x là một số nguyên tố” là một mệnh đề chứa biến

Với x = 3, mệnh đề P(x): “3 là một số nguyên tố” là mệnh đề đúng.

Với x = 8, mệnh đề P(x): “8 là một số nguyên tố” là mệnh đề sai.

3. Phủ định của một mệnh đề

• Cho mệnh đề P. Mệnh đề “Không phải P” được gọi là mệnh đề phủ định của mệnh đề P và kí hiệu là $\overline{P}$.

Mệnh đề $\overline{P}$ đúng khi P sai, và ngược lại.

Ví dụ:

+ A: “69420 là một số lẻ” là mệnh đề sai.

Mệnh đề phủ định $\overline{A}$: “69420 không phải một số lẻ”, $\overline{A}$ là mệnh đề đúng.

Chú ý: Để phủ định một mệnh đề, ta chỉ cần thêm (hoặc bớt) từ “không” (hoặc “không phải”) vào trước vị ngữ của mệnh đề đó.

4. Mệnh đề kéo theo

• Cho hai mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, được kí hiệu là P ⇒ Q.

Mệnh đề P ⇒ Q chỉ sai khi P đúng Q sai, và đúng trong tất cả các trường hợp còn lại.

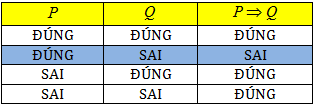
Nhận xét: Tùy theo nội dung cụ thể, đôi khi người ta còn phát biểu mệnh đề P ⇒ Q là “P kéo theo Q” hay “P suy ra Q” hay “Vì P nên Q”…

Ví dụ:

+ Xét hai mệnh đề: P: “Tứ giác ABCD có bốn cạnh bằng nhau” và Q: “Tứ giác ABCD là hình thoi”.

+ Mệnh đề P ⇒ Q được phát biểu là: “Nếu tứ giác ABCD có bốn cạnh bằng nhau thì tứ giác ABCD là hình thoi”. Mệnh đề này là mệnh đề đúng.

Nhận xét: Các định lí toán học thường phát biểu ở dạng mệnh đề kéo theo P ⇒ Q.

Khi đó ta nói:

P là giả thiết, Q là kết luận của định lí, hay P là điều kiện đủ để có Q, hoặc Q là điều kiện cần để có P.

Ví dụ:

Ta có định lý: Nếu một tứ giác có tổng số đo hai góc đối diện nhau bằng 180⁰ thì tứ giác đó nội tiếp được đường tròn.

Khi đó, ta nói:

+ Tứ giác có tổng số đo hai góc đối diện nhau bằng 180⁰ là điều kiện đủ để tứ giác đó nội tiếp được đường tròn.

+ Tứ giác đó nội tiếp được đường tròn là điều kiện cần để tứ giác có tổng số đo hai góc đối diện nhau bằng 180⁰.

5. Mệnh đề đảo. Mệnh đề tương đương

• Mệnh đề Q ⇒ P là mệnh đề đảo của mệnh đề P ⇒ Q.

Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều đúng, P và Q là hai mệnh đề tương đương và kí hiệu P ⇔ Q.

Nhận xét: Mệnh đề P ⇔ Q có thể phát biểu ở những dạng như sau:

+ “P tương đương Q”;

+ “P là điều kiện cần và đủ để có Q”;

+ “P khi và chỉ khi Q”;

+ “P nếu và chỉ nếu Q”.

Ví dụ: Với P: “Tứ giác ABCD có bốn cạnh bằng nhau” và Q: “Tứ giác ABCD là hình thoi” thì P ⇒ Q: “Tứ giác ABCD có bốn cạnh bằng nhau thì tứ giác ABCD là hình thoi” là mệnh đề đúng, và Q ⇒ P: “Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD có bốn cạnh bằng nhau” cũng là mệnh đề đúng.

Do đó P ⇔ Q, phát biểu:

+ “Tứ giác ABCD là hình thoi khi và chỉ khi tứ giác ABCD có bốn cạnh bằng nhau”.

+ “Tứ giác ABCD là hình thoi là điều kiện cần và đủ để tứ giác ABCD có bốn cạnh bằng nhau”.

Chú ý: Trong toán học, những câu khẳng đỉnh đúng phát biểu ở dạng “P ⇔ Q” cũng được coi là một mệnh đề toán học, gọi là mệnh đề tương đương.

6. Kí hiệu ∀ và ∃

• Kí hiệu ∀ đọc là “với mọi”.

• Kí hiệu ∃ đọc là “tồn tại”, hoặc “có một” (tồn tại một), hoặc “có ít nhất một” (tồn tại ít nhất một).

Ví dụ: Phát biểu các mệnh đề:

+ “$\forall x\in ℝ,x^2+1>0$”: Với mọi số thực x thì x² + 1 luôn lớn hơn 0.

+ “$\exists x\in \mathbb{N},2x=3$”: Tồn tại số tự nhiên x sao cho 2x bằng 3.

• Phủ định của mệnh đề “$\forall x\in X,P\left(x\right)$” là mệnh đề “$\exists x\in X,\overline{P\left(x\right)}$”.

• Phủ định của mệnh đề “$\exists x\in X,P\left(x\right)$” là mệnh đề “$\forall x\in X,\overline{P\left(x\right)}$”.

Ví dụ:

+ Phủ định của mệnh đề “$\forall x\in ℝ,x^2+1>0$” là mệnh đề “$\exists x\in ℝ,x^2+1\le 0$”.

+ Phủ định của mệnh đề “$\exists x\in \mathbb{N},2x=3$” là mệnh đề “$\forall x\in \mathbb{N},2x\ne 3$”.