Với lời giải SBT Toán 7 trang 74 Tập 1 chi tiết trong Ôn tập chương 4 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Ôn tập chương 4
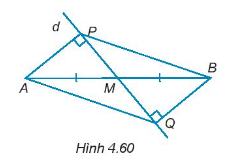
Bài 4.58 trang 74 SBT Toán 7 Tập 1: Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P ∈ d, Q ∈ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:
a) AP = BQ.
b) ∆APB = ∆BQA.
Hướng dẫn giải
a) Xét tam giác vuông PAM và tam giác vuông QBM có:
AM = BM (do M là trung điểm của AB)
(hai góc đối đỉnh)
Do đó, ∆PAM = ∆QBM (cạnh huyền – góc nhọn).
Suy ra AP = BQ.
b) Xét tam giác APB và tam giác BQA có:
AP = BQ (cmt)
(do ∆PAM = ∆QBM)
AB: cạnh chung
Do đó, ∆APB = ∆BQA (c – g – c).
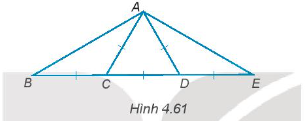
Bài 4.59 trang 74 SBT Toán 7 Tập 1: Cho Hình 4.61, hãy tính số đo các góc của tam giác ABE.
Hướng dẫn giải
Ta có: AD = AC = CD, do đó tam giác ACD là tam giác đều.
Suy ra .
Ta có: (hai góc kề bù)
.
Tam giác ABC có CB = CA nên tam giác ACB cân tại đỉnh C.
Suy ra .
Ta có: (định lí tổng ba góc trong tam giác)
Do đó, .
Suy ra .
Do đó, .
Chứng minh tương tự đối với tam giác ADE cân tại đỉnh D, ta cũng có:
Ta có:
.
Vậy trong tam giác ABE có: ; và .
Bài 4.60 trang 74 SBT Toán 7 Tập 1: Cho hình thang cân ABCD có đáy lớn AD và đáy nhỏ BC thỏa mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD.
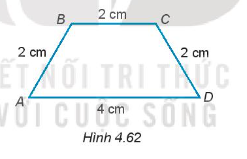
Hướng dẫn giải
Gọi O là trung điểm của AD.
Khi đó, AO = OD = (cm).
Do đó, AB = BC = CD = AO = OD = 2 cm.
Tam giác ABO có AB = BO nên tam giác ABO cân tại đỉnh A.
Suy ra .
Lại có: AD // BC (do ABCD là hình thang cân có AD và BC là đáy)
Suy ra (hai góc so le trong).
Do đó, .
Xét tam giác ABO và tam giác CBO có:
AB = BC (= 2 cm)
(cmt)
BO: cạnh chung
Do đó, ∆ABO = ∆CBO (c – g – c).
Suy ra CO = AO = 2 cm.
Tam giác COD có CD = OD = OC (= 2 cm). Do đó tam giác COD là tam giác đều.
Suy ra .
Ta có: (BC // AD, hai góc ở vị trí trong cùng phía)
Suy ra .
Do ABCD là hình thang cân với AD và BC là đáy.
Vậy và .
Xem thêm các bài giải sách bài tập Toán 7 Kết nối tri thức hay, chi tiết khác:
Giải SBT Toán 7 trang 71 Tập 1
Giải SBT Toán 7 trang 72 Tập 1
Giải SBT Toán 7 trang 73 Tập 1