Với lời giải SBT Toán 7 trang 72 Tập 1 chi tiết trong Ôn tập chương 4 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Ôn tập chương 4
Câu 6 trang 72 SBT Toán 7 Tập 1: Trong các câu sau đây, câu nào sai?
A. Tam giác tù là tam giác có một góc có số đo lớn hơn 90°.
B. Tam giác vuông là tam giác có một góc có số đo bằng 90°.
C. Tam giác cân là tam giác có ba góc có số đo bằng 60°.
D. Tam giác nhọn là tam giác có ba góc có số đo nhỏ hơn 90°.
Hướng dẫn giải
Đáp án đúng là: C
Tam giác tù có một góc tù và góc tù thì có số đo lớn hơn 90°, do đó câu A đúng.
Tam giác vuông là tam giác có một góc vuông nên câu B đúng.
Tam giác nhọn là tam giác có cả ba góc đều là góc nhọn, số đo góc nhọn nhỏ hơn 90°.
Vậy câu D đúng.
Tam giác cân là tam giác có hai cạnh bằng nhau. Trong tam giác cân, hai góc ở đáy bằng nhau.
Vậy câu C sai.
Câu 7 trang 72 SBT Toán 7 Tập 1: Trong các câu sau đây, câu nào đúng?
A. Đường thẳng đi qua trung điểm của đoạn thẳng AB là đường trung trực của đoạn thẳng AB.
B. Đường thẳng vuông góc với đoạn thẳng AB là đường trung trực của đoạn thẳng AB.
C. Tập hợp các điểm các đều hai điểm phân biệt A và B là đường thẳng đi qua trung điểm của đoạn thẳng AB.
D. Đường thẳng đi qua trung điểm và vuông góc với đoạn thẳng AB là đường trung trực của đoạn thẳng AB.
Hướng dẫn giải
Đáp án đúng là: D
Theo định nghĩa, đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
Vậy câu D đúng.
B. Bài tập
Bài 4.51 trang 72 SBT Toán 7 Tập 1: Tính số đo các góc x, y, z, t, v trong Hình 4.55.
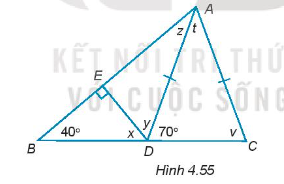
Hướng dẫn giải
Tam giác BED vuông tại E nên .
Suy ra 90° – 40° = 50°.
Ta có: (hai góc kề bù)
.
Lại có: hay x + y = 110°.
Suy ra y = 110° – x = 110° – 50° = 60°.
Tam giác AED vuông tại E nên hay y + z = 90°.
Suy ra z = 90° – y = 90° – 60° = 30°.
Tam giác ADC có AD = AC nên tam giác ADC cân tại đỉnh A.
Suy ra hay v = 70°.
Áp dụng định lí tổng ba góc trong tam giác ADC, ta có:
hay t = 40°.
Vậy x = 50°, y = 60°, z = 30°, v = 70°, t = 40°.
Bài 4.52 trang 72 SBT Toán 7 Tập 1: Trong các câu sau đây, câu nào đúng, câu nào sai?
a) Tam giác nhọn có ba góc đều nhọn.
b) Tam giác vuông có đúng hai góc nhọn.
c) Tam giác tù có đúng một góc nhọn.
d) Trong ba góc của một tam giác tù, góc tù có số đo lớn nhất.
Hướng dẫn giải
Câu a đúng theo định nghĩa tam giác nhọn.
Tam giác vuông có một góc vuông và hai góc còn lại phải là góc nhọn để đảm bảo định lí tổng ba góc trong tam giác do đó câu b đúng.
Tam giác tù có một góc tù và hai góc còn lại là hai góc nhọn nên góc tù có số đo lớn nhất, do đó câu c sai và câu d đúng.
Vậy a), b), d) đúng và c) sai.
Bài 4.53 trang 72 SBT Toán 7 Tập 1: Trong các câu sau đây, câu nào đúng, câu nào sai?
a) Tam giác cân có một góc bằng 60° là tam giác đều.
b) Tam giác cân là tam giác nhọn.
c) Tổng hai góc nhọn của một tam giác vuông bằng 90°.
d) Tam giác vuông cân thì luôn cân tại đỉnh góc vuông và có hai góc nhọn bằng 45°.
Hướng dẫn giải
a) Câu a) đúng.
Giải thích:
+ Giả sử tam giác ABC cân tại đỉnh A có góc ở đáy ![]() = 60°.
= 60°.
Khi đó, .
Theo định lí tổng ba góc trong tam giác, ta có: .
.
Do đó, , nên tam giác ABC cân tại đỉnh C.
Vậy tam giác ABC đều.
+ Giả sử tam giác ABC cân tại đỉnh A có góc ở đỉnh .
Theo định lí tổng ba góc trong tam giác, ta có: .
Mà (do tam giác ABC cân đỉnh A).
Do đó, , suy ra .
Do đó, , nên tam giác ABC cân tại đỉnh C.
Vậy tam giác ABC đều.
b) Câu b) sai.
Chẳng hạn tam giác ABC cân tại đỉnh A có , , đây là tam giác tù.
c) Từ định lí tổng ba góc trong tam giác, ta suy ra tổng hai góc nhọn của một tam giác vuông bằng 90°.
Vậy câu c) đúng.
d) Tam giác vuông cân thì luôn cân tại đỉnh góc vuông và có hai góc nhọn bằng 45° là câu đúng.
Giả sử có tam giác ABC vuông tại A, cân tại B, khi đó , do đó không thỏa mãn định lí tổng ba góc trong tam giác.
Vậy tam giác vuông cân thì luôn cân tại đỉnh góc vuông và từ định lí tổng ba góc và tính chất của tam giác cân, ta tính được số đo hai góc nhọn bằng 45°.
Vậy câu a), c), d) đúng và câu b) sai.
Xem thêm các bài giải sách bài tập Toán 7 Kết nối tri thức hay, chi tiết khác:
Giải SBT Toán 7 trang 71 Tập 1
Giải SBT Toán 7 trang 73 Tập 1
Giải SBT Toán 7 trang 74 Tập 1