Với giải sách bài tập Toán 11 Bài 2: Giới hạn của hàm số sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 2: Giới hạn của hàm số
Bài 12 trang 74 SBT Toán 11 Tập 1: Giả sử và (L, M ∈ ℝ). Phát biểu nào sau đây là sai?
Lời giải:
Đáp án đúng là: D
Với và (L, M ∈ ℝ) thì (nếu M ≠ 0).
Do vậy đáp án D sai vì thiếu điều kiện M ≠ 0.
A. Nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L thì .
B. Nếu với dãy số (xn) bất kì, xn → x0, ta có f(xn) → L thì .
C. Nếu với dãy số (xn) bất kì, x0 < xn < b và xn → L, ta có f(xn) → x0 thì .
D. Nếu với dãy số (xn) bất kì, xn < x0 và xn → x0, ta có f(xn) → L thì .
Lời giải:
Đáp án đúng là: A
Theo lí thuyết, ta có: Cho hàm số y = f(x) xác định trên khoảng (x0; b), nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L thì .
Bài 14 trang 75 SBT Toán 11 Tập 1: Với c, k là các hằng số và k nguyên dương thì
A. .
B. .
C. .
D. hoặc .
Lời giải:
Đáp án đúng là: A
Với c, k là các hằng số và k nguyên dương, ta luôn có .
Bài 15 trang 75 SBT Toán 11 Tập 1: Phát biểu nào sau đây là đúng?
A. Nếu thì .
B. Nếu thì L ≥ 0.
c. Nếu f(x) ≥ 0 và thì L ≥ 0 và .
D. Nếu thì L ≥ 0 và .
Lời giải:
Đáp án đúng là: C
Theo lí thuyết ta có: Nếu f(x) ≥ 0 và thì L ≥ 0 và .
A. Nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L thì .
B. Nếu với dãy số (xn) bất kì, xn < a và xn → +∞, ta có f(xn) → L thì .
C. Nếu với dãy số (xn) bất kì, xn > a, ta có f(xn) → L thì .
D. Nếu với dãy số (xn) bất kì, xn > a và xn → L, ta có f(xn) →+∞ thì .
Lời giải:
Đáp án đúng là: A
Theo lí thuyết, ta có: Cho hàm số y = f(x) xác định trên khoảng (a ; + ∞), nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L thì .
Bài 17 trang 75 SBT Toán 11 Tập 1: Sử dụng định nghĩa, chứng minh rằng:
a) .
b) .
Lời giải:
a) Xét hàm số f(x) = x3. Giả sử (xn) là dãy số bất kì, thỏa mãn limxn = – 2.
Ta có limf(xn) = .
Vậy .
b) Xét hàm số .
Giả sử (xn) là dãy số bất kì, thỏa mãn xn ≠ – 2 và lim xn = – 2.
Ta có .
Vậy .
Bài 18 trang 75 SBT Toán 11 Tập 1: Cho , chứng minh rằng:
a) ;
b) ;
c) .
Lời giải:
a) .
b) .
c) .
Bài 19 trang 76 SBT Toán 11 Tập 1: Quan sát đồ thị hàm số ở Hình 2 và cho biết các giới hạn sau: .
Lời giải:
Dựa vào đồ thị hàm số, ta có:
;
;
;
.
Bài 20 trang 76 SBT Toán 11 Tập 1: Tính các giới hạn sau:
a) ; b) ;
c) ; d) ;
e) ; g) .
Lời giải:
a) = – 4 – 3 + 1 = – 6.
b) .
c) Vì .
Do đó, .
d) Vì
và 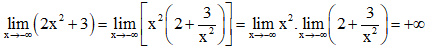
Do đó, .
e) Vì ; và x – 2 > 0 với mọi x > 2.
Do đó, .
g) Vì ; và x + 2 > 0 với mọi x > – 2.
Do đó, .
Bài 21 trang 76 SBT Toán 11 Tập 1: Tính các giới hạn sau:
a) ; b) ;
c) ; d) ;
e) ; g) .
Lời giải:
a) .
b) .
c)
d)
.
e) .
g) .
Bài 22 trang 76 SBT Toán 11 Tập 1: Cho . Tính:
a) ;
b) .
Lời giải:
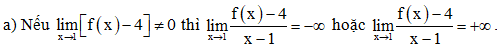
Điều này mâu thuẫn với giả thiết .
b) Ta có .
Bài 23 trang 76 SBT Toán 11 Tập 1: Cho hàm số f(x) thoả mãn . Tính .
Lời giải:
Ta có
.
Vậy .
Bài 24 trang 76 SBT Toán 11 Tập 1: Cho số thực a và hàm số (x) thoả mãn . Chứng minh rằng:
.
Lời giải:
Ta có
.
Vậy .
Lời giải:
Ta có g(10) = 45 . 102 – 103.
Khi đó
.
Vậy = 600.
Từ kết quả trên, ta thấy tốc độ tăng người bệnh ngay tại thời điểm t = 10 ngày là 600 người/ngày.
Xem thêm các bài giải SBT Toán 11 Cánh diều hay, chi tiết khác:
Bài 1: Đường thẳng và mặt phẳng trong không gian
Bài 2: Hai đường thẳng song song trong không gian
Lý thuyết Giới hạn của hàm số
I. Giới hạn hữu hạn của hàm số tại một điểm
1. Định nghĩa
Cho khoảng K chứa điểm x0và hàm số f(x) xác định trên K hoặc trên K∖{x0}. Hàm số f(x)có giới hạn là số L khi x dần tới x0 nếu với dãy số (xn)bất kì, xn∈K∖{x0} và xn→x0, ta cóf(xn)→L
Kí hiệu limx→x0f(x)=L hay f(x)→L, khi xn→x0.
2. Phép toán trên giới hạn hữu hạn của hàm số
a, Nếu limx→x0f(x)=L và limx→x0g(x)=M(L,M∈R)thì
limx→x0[f(x)±g(x)]=L±M
limx→x0[f(x).g(x)]=L.M
limx→x0[f(x)g(x)]=LM(M≠0)
b, Nếu f(x)≥0 với mọi x∈(a;b)∖{x0} và limx→x0f(x)=L thì L≥0 và limx→x0√f(x)=√L.
3. Giới hạn một phía
- Cho hàm số y=f(x) xác định trên khoảng (a;x0). Số L được gọi là giới hạn bên trái của hàm số y=f(x) khi x→x0 nếu với dãy số (xn) bất kì thỏa mãn a<xn<x0 và xn→x0 ta có f(xn)→L, kí hiệu limx→x0−f(x)=L.
- Cho hàm số y=f(x) xác định trên khoảng (x0;b). Số L là giới hạn bên của hàm số y=f(x) khi x→x0 nếu với dãy số (xn)bất kì thỏa mãn x0<xn<b và xn→x0 ta có f(xn)→L, kí hiệu limx→x0+f(x)=L.
*Nhận xét: limx→x0f(x)=L⇔limx→x0−f(x)=limx→x0+f(x)=L
II. Giới hạn hữu hạn của hàm số tại vô cực
- Cho hàm số y=f(x)xác định trên khoảng (a;+∞). Ta nói hàm số f(x) có giới hạn là số L khi x→+∞ nếu với dãy số (xn)bất kì xn>a và xn→+∞ta có f(xn)→L, kí hiệu limx→+∞f(x)=L hay f(x)→L khi x→+∞.
- Cho hàm số y=f(x) xác định trên khoảng (−∞;b). Ta nói hàm số f(x) có giới hạn là số L khi x→−∞ nếu với dãy số (xn)bất kì xn<b và xn→−∞ta có f(xn)→L, kí hiệu limx→−∞f(x)=L hay f(x)→L khi x→−∞.
* Nhận xét:
- Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.
- Với c là hằng số, k là một số nguyên dương ta có:
limx→+∞c=c, limx→−∞c=c,limx→+∞(cxk)=0,limx→−∞(cxk)=0.
III. Giới hạn vô cực (một phía) của hàm số tại một điểm
- Cho hàm số y=f(x)xác định trên khoảng (a;+∞). Ta nói hàm số f(x)có giới hạn +∞ khi x→a+ nếu với dãy số (xn) bất kì, xn>a và xn→ata có f(xn)→+∞.
Kí hiệu limx→a+f(x)=+∞hay f(x)→+∞ khi x→a+
- Các giới hạn limx→a+f(x)=−∞,limx→a−f(x)=+∞,limx→a−f(x)=−∞ được định nghĩa tương tự.
IV. Giới hạn vô cực của hàm số tại vô cực
- Cho hàm số y=f(x) xác định trên khoảng (a;x0). Ta nói hàm số f(x)có giới hạn +∞ khi x→x0 về bên trái nếu với dãy số (xn)bất kì, xn>a và xn→+∞ ta có f(xn)→+∞, kí hiệu limx→+∞f(x)=+∞.
Kí hiệu limx→+∞f(x)=+∞ hay f(x)→+∞ khi x→+∞.
- Các giới hạn limx→+∞f(x)=−∞,limx→−∞f(x)=+∞,limx→−∞f(x)=−∞ được định nghĩa tương tự.
* Chú ý: