Với lời giải SBT Toán 11 trang 76 Tập 1 chi tiết trong Bài 2: Giới hạn của hàm số sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 2: Giới hạn của hàm số
Bài 19 trang 76 SBT Toán 11 Tập 1: Quan sát đồ thị hàm số ở Hình 2 và cho biết các giới hạn sau: .
Lời giải:
Dựa vào đồ thị hàm số, ta có:
;
;
;
.
Bài 20 trang 76 SBT Toán 11 Tập 1: Tính các giới hạn sau:
a) ; b) ;
c) ; d) ;
e) ; g) .
Lời giải:
a) = – 4 – 3 + 1 = – 6.
b) .
c) Vì .
Do đó, .
d) Vì
và 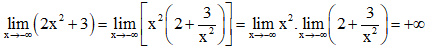
Do đó, .
e) Vì ; và x – 2 > 0 với mọi x > 2.
Do đó, .
g) Vì ; và x + 2 > 0 với mọi x > – 2.
Do đó, .
Bài 21 trang 76 SBT Toán 11 Tập 1: Tính các giới hạn sau:
a) ; b) ;
c) ; d) ;
e) ; g) .
Lời giải:
a) .
b) .
c)
d)
.
e) .
g) .
Bài 22 trang 76 SBT Toán 11 Tập 1: Cho . Tính:
a) ;
b) .
Lời giải:
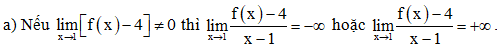
Điều này mâu thuẫn với giả thiết .
b) Ta có .
Bài 23 trang 76 SBT Toán 11 Tập 1: Cho hàm số f(x) thoả mãn . Tính .
Lời giải:
Ta có
.
Vậy .
Bài 24 trang 76 SBT Toán 11 Tập 1: Cho số thực a và hàm số (x) thoả mãn . Chứng minh rằng:
.
Lời giải:
Ta có
.
Vậy .
Lời giải:
Ta có g(10) = 45 . 102 – 103.
Khi đó
.
Vậy = 600.
Từ kết quả trên, ta thấy tốc độ tăng người bệnh ngay tại thời điểm t = 10 ngày là 600 người/ngày.
Xem thêm lời giải sách bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 12 trang 74 SBT Toán 11 Tập 1: Giả sử và (L, M ∈ ℝ). Phát biểu nào sau đây là sai?....
Bài 14 trang 75 SBT Toán 11 Tập 1: Với c, k là các hằng số và k nguyên dương thì....
Bài 15 trang 75 SBT Toán 11 Tập 1: Phát biểu nào sau đây là đúng?....
Bài 17 trang 75 SBT Toán 11 Tập 1: Sử dụng định nghĩa, chứng minh rằng:....
Bài 18 trang 75 SBT Toán 11 Tập 1: Cho , chứng minh rằng:...
Bài 20 trang 76 SBT Toán 11 Tập 1: Tính các giới hạn sau:...
Bài 21 trang 76 SBT Toán 11 Tập 1: Tính các giới hạn sau:...
Bài 22 trang 76 SBT Toán 11 Tập 1: Cho . Tính:...
Bài 23 trang 76 SBT Toán 11 Tập 1: Cho hàm số f(x) thoả mãn . Tính . .....
Bài 24 trang 76 SBT Toán 11 Tập 1: Cho số thực a và hàm số (x) thoả mãn . Chứng minh rằng:...
Xem thêm các bài giải SBT Toán 11 Cánh diều hay, chi tiết khác: