Với giải sách bài tập Toán 11 Bài tập cuối chương 2  sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài tập cuối chương 2

Giải SBT Toán 11 trang 56

Bài 47 trang 56 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết u_n = 5ⁿ – n. Số hạng u_{n + 1} là:

A. 5^{n + 1} – n – 1.

B. 5^{n + 1} – n + 1.

C. 5ⁿ – n + 1.

D. 5ⁿ – n – 1.  

Lời giải:

Đáp án đúng là: A

Ta có: u_{n + 1} = 5^{n + 1} – (n + 1) = 5^{n + 1} – n – 1.

Bài 48 trang 56 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết u₁ = 2, $u_n=\frac{1}{3}\left(u_{n-1}+1\right)$  với n ≥  2. Số hạng u₄ bằng:

A. u₄ = 1.

B. $u_4=\frac{2}{3}$ .

C. $u_4=\frac{14}{27}$ .

D. $u_4=\frac{5}{9}$ .

Lời giải:

Đáp án đúng là: D

Ta có $u_2=\frac{1}{3}\left(u_{2-1}+1\right)=\frac{1}{3}\left(u_1+1\right)=\frac{1}{3}\left(2+1\right)=1$ ;

$u_3=\frac{1}{3}\left(u_{3-1}+1\right)=\frac{1}{3}\left(u_3+1\right)=\frac{1}{3}\left(1+1\right)=\frac{2}{3}$;

$u_4=\frac{1}{3}\left(u_{4-1}+1\right)=\frac{1}{3}\left(u_3+1\right)=\frac{1}{3}\left(\frac{2}{3}+1\right)=\frac{5}{9}$.

Bài 49 trang 56 SBT Toán 11 Tập 1: Trong các dãy số (u_n) với số hạng tổng quát sau, dãy số tăng là:

A. $u_n=\frac{2}{3^n}$ .

B. $u_n=\frac{3}{n}$ .

C. u_n = 2ⁿ.

D. u_n = (– 2)ⁿ.

Lời giải:

Trong các dãy số đã cho, ta thấy dãy số (u_n) với u_n = 2ⁿ là dãy số tăng.

Thật vậy, ta có u_{n + 1} = 2^{n + 1} = 2 . 2ⁿ.

Khi đó, u_{n + 1} – u_n = 2 . 2ⁿ – 2ⁿ = 2ⁿ > 0 với mọi n ∈ ℕ^*, tức là u_{n + 1} > u_n với mọi n ∈ ℕ^*.

Vậy dãy số (u_n) với u_n = 2ⁿ là dãy số tăng.

Bài 50 trang 56 SBT Toán 11 Tập 1: Tổng 20 số tự nhiên liên tiếp chia hết cho 3 tính từ số 3 là:

A. 1 320.

B. 660.

C. 630.

D. 1 260.

Lời giải:

Đáp án đúng là: C

20 số tự nhiên liên tiếp chia hết cho 3 tính từ số 3 lập thành một cấp số cộng với số hạng đầu u₁ = 3 và công sai d = 3.

Khi đó, tổng của 20 số này là: 

Giải SBT Toán 11 trang 57

Bài 51 trang 57 SBT Toán 11 Tập 1: Trong các dãy số (u_n) với số hạng tổng quát sau, dãy số nào là cấp số nhân?

A. $u_n=\frac{1}{5^n}$ .

B. $u_n=1+\frac{1}{5n}$ .

C. $u_n=\frac{1}{5^n}+1$ .

D. $u_n=\frac{1}{n^2}$ .

Lời giải:

Đáp án đúng là: A

Xét dãy số (u_n) với $u_n=\frac{1}{5^n}$ .

Ta có: $u_1=\frac{1}{5^1}=\frac{1}{5}$

$u_{n+1}=\frac{1}{5^{n+1}}=\frac{1}{5^n.5}=\frac{1}{5}.\frac{1}{5^n}=\frac{1}{5}{u}_n$ không đổi với mọi n ∈ ℕ^*.

Vậy dãy số (u_n) với $u_n=\frac{1}{5^n}$  là cấp số nhân với số hạng đầu $u_1=\frac{1}{5}$  và công bội $q=\frac{1}{5}$ .

Bài 52 trang 57 SBT Toán 11 Tập 1: Cho cấp số nhân (u_n) có tất cả các số hạng đều không âm và u₂ = 6, u₄ = 24. Tổng 10 số hạng đầu của (u_n) là:

A. 3(1 – 2¹⁰).

B. 3(2⁹ – 1).

C. 3(2¹⁰ – 1).

D. 3(1 – 2⁹).

Lời giải:

Đáp án đúng là: C

Giả sử q là công bội của cấp số nhân (u_n) (điều kiện q ≠ 0).

Ta có: u₂ = u₁q = 6; u₄ = u₁q³ = 24, suy ra $\frac{u_4}{u_2}=\frac{u_1{q}^3}{u_{1}q}=q^2=\frac{24}{6}=4$ .

Do đó, q = ± 2.

Mà cấp số nhân (u_n) có tất cả các số hạng đều không âm nên q = 2.

Từ u₂ = u₁q = 6, suy ra u₁ = $\frac{6}{q}$  = 3.

Vậy tổng 10 số hạng đầu của (u_n) là 

Bài 53 trang 57 SBT Toán 11 Tập 1: Tổng 1 + 11 + 101 + 1001 + ...... + 100...01 (12 số hạng) bằng:

A. $\frac{{10}^{11}+107}{9}$ .

B. $\frac{{10}^{12}+98}{9}$ .

C. $\frac{{10}^{12}+107}{9}$ .

D. $\frac{{10}^{11}+98}{9}$ .

Lời giải:

Đáp án đúng là: B

Ta có 1 + 11 + 101 + 1001 + ...... + 100...01

= 1 + (10 + 1) + (100 + 1) + (1000 + 1) + ... + (100...0 + 1)

= 12 + (10 + 100 + 1000 + ... + 100...0)

= 12 + (10 + 10² + 10³ + ... + 10¹¹)

$=12+\frac{10\left(1-{10}^{11}\right)}{1-10}$

$=\frac{108}{9}+\frac{{10}^{12}-10}{9}$

$=\frac{{10}^{12}+98}{9}$.

Bài 54 trang 57 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết 

a) Viết sáu số hạng đầu của dãy số.

b) Chứng minh rằng u_{n + 6} = u_n với mọi n ≥ 1.

c) Tính tổng 27 số hạng đầu của dãy số.

Lời giải:

a) Ta có  ;

Vậy sáu số hạng đầu của dãy số là: 0; $-\frac{\sqrt{3}}{2}$ ; $-\frac{\sqrt{3}}{2}$ ; 0; $\frac{\sqrt{3}}{2}$ ; $\frac{\sqrt{3}}{2}$ . 

b) Ta có

 với mọi n ≥ 1.

c) Vì u_{n + 6} = u_n với mọi n ≥ 1 nên

u₁ + u₂ + u₃ + ... + u₂₇ = 4 . (u₁ + u₂ + u₃ + u₄ + u₅ + u₆) + u₁ + u₂ + u₃

= $-\sqrt{3}$ .

Bài 55 trang 57 SBT Toán 11 Tập 1: Cho dãy số (u_n) có tổng n số hạng đầu là $S_n=\frac{n\left(-1-5n\right)}{2}$  với n ∈ ℕ^*.

a) Tính u₁, u₂ và u₃.

b) Tìm công thức của số hạng tổng quát u_­n.

c) Chứng minh rằng dãy số (u_n) là một cấp số cộng.

Lời giải:

a) Ta có: $u_1=S_1=\frac{1.\left(-1-5.1\right)}{2}=-3$ .

Vì $u_1+u_2=S_2=\frac{2.\left(-1-5.2\right)}{2}=-11$  nên u₂ = S₂ – u₁ = – 11 – (– 3) = – 8.

Vì $S_2+u_3=S_3=\frac{3\left(-1-5.3\right)}{2}=-24$  nên u₃ = S₃ – S₂ = – 24 – (– 11) = – 13.

b) Ta có: u_n = S_n – S_{n – 1} =

$=\frac{-n-5n^2-\left(n-1\right)\left(-1-5n+5\right)}{2}$$=\frac{-n-5n^2-\left(-n-5n^2+5n+1+5n-5\right)}{2}$

$=\frac{-10n+4}{2}=2-5n$.

Vậy u_n = 2 – 5n.

c) Ta có: 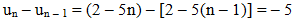, với mọi n ≥ 2.

Vậy dãy số (u_n) là một cấp số cộng.

Bài 56 trang 57 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết u₁ = 1, u₂ = 2, u_{n + 1} = 2u_n – u_{n – 1} + 2 với n ≥ 2.

a) Viết năm số hạng đầu của dãy số.

b) Đặt v_n = u_{n + 1} – u_n với n ∈ ℕ^*. Chứng minh rằng dãy số (v_n) là cấp số cộng.

c) Tìm công thức của v_n, u_n tính theo n.

Lời giải:

a) Ta có u₁ = 1, u₂ = 2, u₃ = u_{2 + 1} = 2u₂ – u_{2 – 1} + 2 = 2 . 2 – 1 + 2 = 5,

u₄ = u_{3 + 1} = 2u₃ – u_{3 – 1} + 2 = 2 . 5 – 2 + 2 = 10,

u₅ = u_{4 + 1} = 2u₄ – u_{4 – 1} + 2 = 2 . 10 – 5 + 2 = 17.

Vậy năm số hạng đầu của dãy số là: 1; 2; 5; 10; 17.

b) Từ công thức u_{n + 1} = 2u_n – u_{n – 1} + 2 suy ra u_{n + 1} – u_n = u_n – u_{n – 1} + 2.

Mà v_n = u_{n + 1} – u_n và v_{n – 1} = u_{n – 1 + 1} – u_{n – 1} = u_n – u_{n – 1}.

Do đó, v_n = v_{n – 1} + 2 với n ≥ 2.

Vậy dãy số (v_n) là một cấp số cộng có số hạng đầu v₁ = u₂ – u₁ = 1 và công sai d = 2.

c) Từ kết quả câu b, ta có: v_n = v₁ + (n – 1)d = 1 + (n – 1) . 2 = – 1 + 2n.

Lại có: v₁ = u₂ – u₁

            v₂ = u₃ – u₂

            ...

            v_{n – 2} = u_{n – 1} – u_{n – 2}

            v_{n – 1} = u_n – u_{n – 1}

Cộng theo từng vế của n − 1 đẳng thức trên, ta có:

v₁ + v₂ + ... + v_{n – 2} + v_{n – 1} = – u₁ + u_n  

         $\iff \frac{\left(v_1+v_{n-1}\right)\left(n-1\right)}{2}=-1+u_n$

⇔ (n – 1)² = u_n – 1

⇔ u_n = 1 + (n – 1)².

Vậy u_n = 1 + (n – 1)² và v_n = – 1 + 2n với mọi n ∈ ℕ^*.

Bài 57 trang 57 SBT Toán 11 Tập 1: Cho dãy số (u_n), biết u₁ = – 2, $u_{n+1}=\frac{n+1}{2n}{u}_n$  với n ∈ ℕ^*. Đặt $v_n=\frac{u_n}{n}$  với n ∈ ℕ^*.

a) Chứng minh rằng dãy số (v_n) là cấp số nhân. Tìm số hạng đầu, công bội của cấp số nhân đó.

b) Tìm công thức của u_n tính theo n.

Lời giải:

a) Ta có $v_1=\frac{u_1}{1}=\frac{-2}{1}=-2$ ;

$v_{n+1}=\frac{u_{n+1}}{n+1}=\left(\frac{n+1}{2n}{u}_n\right):\left(n+1\right)=\frac{1}{2}.\frac{u_n}{n}=\frac{1}{2}{v}_n$ với mọi n ∈ ℕ^*.

Vậy dãy số (v_n) là một cấp số nhân có số hạng đầu v₁ = – 2 và công bội $q=\frac{1}{2}$ .

b) Từ kết quả của câu a) suy ra $v_n=v_1.q^{n-1}=\left(-2\right).{\left(\frac{1}{2}\right)}^{n-1}=-{\left(\frac{1}{2}\right)}^{n-2}$ .

Từ $v_n=\frac{u_n}{n}$ , suy ra $u_n=n.v_n=-n.{\left(\frac{1}{2}\right)}^{n-2}$  với mọi n ≥ 2.

Giải SBT Toán 11 trang 58

Bài 58 trang 58 SBT Toán 11 Tập 1: Một công ty mua một chiếc máy với giá 1 tỉ 200 triệu đồng. Công ty nhận thấy, trong vòng 5 năm đầu, tốc độ khấu hao là 25%/năm (tức là sau mỗi một năm, giá trị còn lại của chiếc máy bằng 75% giá trị của năm trước đó).

a) Viết công thức tính giá trị của chiếc máy đó sau 1 năm, 2 năm.

b) Sau 5 năm, giá trị của chiếc máy đó còn khoảng bao nhiêu triệu đồng (làm tròn đến hàng đơn vị)?

Lời giải:

a) Giá trị của chiếc máy đó sau 1 năm là:

1 200 . 0,75 = 900 (triệu đồng).

Giá trị của chiếc máy đó sau 2 năm là:

1 200 . 0,75 . 0, 75 = 1 200 . 0,75² = 675 (triệu đồng).

b) Sau 5 năm, giá trị chiếc máy đó còn là:

1 200 . 0,75⁵ ≈ 285 (triệu đồng).

Bài 59 trang 58 SBT Toán 11 Tập 1: Một hình vuông có diện tích bằng 1 đơn vị diện tích. Chia hình vuông đó thành 9 hình vuông bằng nhau và tô màu hình vuông ở chính giữa. Với mỗi hình vuông nhỏ chưa được tô màu, lại chia thành 9 hình vuông bằng nhau và tô màu hình vuông ở chính giữa. Cứ như thế, quá trình trên được lặp lại.

a) Tính tổng diện tích phần đã được tô màu ở hình thứ nhất, thứ hai, thứ ba.

b) Dự đoán công thức tính tổng diện tích phần đã được tô màu ở hình thứ n.

Lời giải:

a) Diện tích phần đã được tô màu ở hình thứ nhất, hình thứ hai, hình thứ ba lần lượt là:

$1-\frac{8}{9}=\frac{1}{9};1-{\left(\frac{8}{9}\right)}^2=\frac{17}{81};1-{\left(\frac{8}{9}\right)}^3=\frac{217}{729}$.

b) Gọi S_n là diện tích phần đã được tô màu ở hình thứ n.

Ta có: S_n = 1 – ${\left(\frac{8}{9}\right)}^n$ .

Xem thêm các bài giải SBT Toán 11 Cánh diều hay, chi tiết khác:

Bài 3: Cấp số nhân

Bài tập cuối chương 2

Bài 1: Giới hạn của dãy số

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục

Bài tập cuối chương 3