Với giải Bài 55 trang 57 SBT Toán lớp 11 Cánh diều chi tiết trong Bài tập cuối chương 2 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11 . Mời các bạn đón xem:
Giải SBT Toán 11 Bài tập cuối chương 2
Bài 55 trang 57 SBT Toán 11 Tập 1: Cho dãy số (un) có tổng n số hạng đầu là với n ∈ ℕ*.
a) Tính u1, u2 và u3.
b) Tìm công thức của số hạng tổng quát un.
c) Chứng minh rằng dãy số (un) là một cấp số cộng.
Lời giải:
a) Ta có: .
Vì nên u2 = S2 – u1 = – 11 – (– 3) = – 8.
Vì nên u3 = S3 – S2 = – 24 – (– 11) = – 13.
b) Ta có: un = Sn – Sn – 1 =
.
Vậy un = 2 – 5n.
c) Ta có: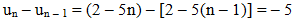 
, với mọi n ≥ 2.
Vậy dãy số (un) là một cấp số cộng.
Xem thêm lời giải sách bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 47 trang 56 SBT Toán 11 Tập 1: Cho dãy số (un) biết un = 5n – n. Số hạng un + 1 là:....
Bài 48 trang 56 SBT Toán 11 Tập 1: Cho dãy số (un) biết u1 = 2, với n ≥ 2. Số hạng u4 bằng:...
Bài 50 trang 56 SBT Toán 11 Tập 1: Tổng 20 số tự nhiên liên tiếp chia hết cho 3 tính từ số 3 là:...
Bài 54 trang 57 SBT Toán 11 Tập 1: Cho dãy số (un) biết ![Cho dãy số (un) biết un = cos [(2n + 1) π/6]](https://vietjack.com/sbt-toan-11-cd/images/bai-54-trang-57-sbt-toan-lop-11-tap-1.PNG)
....
Bài 55 trang 57 SBT Toán 11 Tập 1: Cho dãy số (un) có tổng n số hạng đầu là với n ∈ ℕ*....
Bài 57 trang 57 SBT Toán 11 Tập 1: Cho dãy số (un), biết u1 = – 2, với n ∈ ℕ*. Đặt với n ∈ ℕ*.....
Xem thêm các bài giải SBT Toán 11 Cánh diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
