Với lời giải SBT Toán 7 trang 46 Tập 1 chi tiết trong Bài 11: Định lí và chứng minh định lí sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 11: Định lí và chứng minh định lí

Bài 3.27 trang 46 SBT Toán 7 Tập 1: Cho định lí: “Một đường thẳng cắt hai đường thẳng song song thì tạo thành cặp góc so le trong bằng nhau”.

a) Hãy chỉ ra giả thiết và kết luận của định lí.

b) Vẽ hình minh họa và ghi giả thiết, kết luận bằng kí hiệu.

Lời giải:

a) Giả thiết: Một đường thẳng cắt hai đường thẳng song song.

Kết luận: Hai góc so le trong tạo thành bằng nhau.

b)

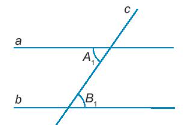
Giả thiết: a // b; c cắt a tại A, c cắt b tại B, tạo thành một cặp góc so le trong $\widehat{A_1}; \widehat{B_1}$.

Kết luận: $\widehat{A_1}=\widehat{B_1}$.

Bài 3.28 trang 46 SBT Toán 7 Tập 1: Cho định lí: “Một đường thẳng cắt hai đường thẳng tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song”.

a) Hãy chỉ ra giả thiết và kết luận của định lí.

b) Vẽ hình minh họa và ghi giả thiết, kết luận bằng kí hiệu.

Lời giải:

a) Giả thiết: Một đường thẳng cắt hai đường thẳng tạo thành cặp góc so le trong bằng nhau.

Kết luận: hai đường thẳng đó song song.

b)

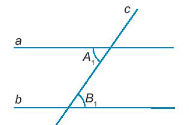
Giả thiết: c cắt a tại A, c cắt b tại B, tạo thành cặp góc so le trong $\widehat{A_1};\widehat{B_1}$ và $\widehat{A_1}=\widehat{B_1}$

Kết luận: a // b.

Bài 3.29 trang 46 SBT Toán 7 Tập 1: Cho định lí: “Tia đối của tia phân giác của một góc là tia phân giác của góc đối đỉnh với góc đó”. Hãy vẽ hình ghi giả thiết, kết luận và chứng minh định lí đó.

Lời giải:

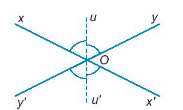
Giả thiết:

- Hai góc xOy; x’Oy’ là hai góc đối đỉnh.

- Ou là tia phân giác của góc xOy, Ou’ là tia đối của tia Ou.

Kết luận: Ou’ là tia phân giác của góc x’Oy’.

Chứng minh định lí:

Ta có:

$\widehat{x\text{'}Ou\text{'}}$ và $\widehat{xOu}$ là hai góc đối đỉnh nên $\widehat{x\text{'}Ou\text{'}}$ = $\widehat{xOu}$.

$\widehat{y\text{'}Ou\text{'}}$ và $\widehat{yOu}$ là hai góc đối đỉnh nên $\widehat{y\text{'}Ou\text{'}}$ = $\widehat{yOu}$.

Lại có: Ou là tia phân giác của $\widehat{xOy}$ nên $\widehat{xOu}$ = $\widehat{yOu}$.

Suy ra: $\widehat{x\text{'}Ou\text{'}}$ = $\widehat{y\text{'}Ou\text{'}}$.

Do đó, Ou’ là tia phân giác của $\widehat{x\text{'}Oy\text{'}}$.

Vậy Ou’ là tia phân giác của $\widehat{y\text{'}Ox\text{'}}$ (điều phải chứng minh).

Bài 3.30 trang 46 SBT Toán 7 Tập 1: Vẽ hình minh họa, ghi giả thiết, kết luận bằng kí hiệu và chứng minh mỗi định lí sau:

a) Hai góc cùng phụ với một góc thứ ba thì bằng nhau.

b) Hai góc cùng bù với một góc thứ ba thì bằng nhau.

Lời giải:

a)

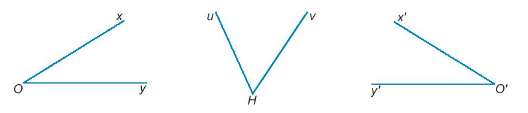
Giả thiết:

$\widehat{xOy}+\widehat{uHv}=90°$; $\widehat{x\text{'}Oy\text{'}}+\widehat{uHv}=90°$

Kết luận:

$\widehat{xOy}=\widehat{x\text{'}Oy\text{'}}$

Chứng minh:

Ta có: $\widehat{xOy}+\widehat{uHv}=90°$ suy ra, $\widehat{x\text{'}Oy\text{'}}+\widehat{uHv}=90°$ (1)

$\widehat{x\text{'}Oy\text{'}}+\widehat{uHv}=90°$ suy ra, $\widehat{x\text{'}Oy\text{'}}=90°-\widehat{uHv}$ (2)

Từ (1) và (2) suy ra: $\widehat{xOy}=\widehat{x\text{'}Oy\text{'}}$ = $90°-\widehat{uHv}$

 Vậy $\widehat{xOy}=\widehat{x\text{'}Oy\text{'}}$

b)

Giả thiết: $\widehat{xOy}+\widehat{uHv}=180°$;$\widehat{x\text{'}Oy\text{'}}+\widehat{uHv}=180°$.

Kết luận: $\widehat{xOy}=\widehat{x\text{'}Oy\text{'}}$

Chứng minh:

Ta có: $\widehat{xOy}+\widehat{uHv}=180°$ suy ra, $\widehat{xOy}=180°-\widehat{uHv}$ (3)

$\widehat{x\text{'}Oy\text{'}}+\widehat{uHv}=180°$ suy ra, $\widehat{x\text{'}Oy\text{'}}=180°-\widehat{uHv}$ (2)

Từ (1) và (2) suy ra: $\widehat{xOy}=\widehat{x\text{'}Oy\text{'}}$ = $180°-\widehat{uHv}$

 Vậy $\widehat{xOy}=\widehat{x\text{'}Oy\text{'}}$

Bài 3.31 trang 46 SBT Toán 7 Tập 1: Cho góc vuông uOv và tia Oy đi qua một điểm trong của góc đó. Vẽ tia Ox sao cho Ou là tia phân giác của góc xOy. Vẽ tia Oz  sao cho Ov là tia phân giác của góc yOz. Chứng minh rằng hai góc xOy và yOz là hai góc kề bù.

Lời giải:

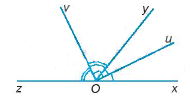
Vì Ou là tia phân giác của góc xOy nên $\widehat{uOy}=\widehat{uOx}=\frac{\widehat{xOy}}{2}$. Hay $\widehat{xOy}=2\widehat{uOy}$

Vì Ov là tia phân giác của góc yOz nên $\widehat{zOv}=\widehat{vOy}=\frac{\widehat{zOy}}{2}$. Hay $\widehat{zOy}=2\widehat{vOy}$

Ta có: $$\begin{gathered} \widehat{xOy}+\widehat{zOy}=2\widehat{uOy}+2\widehat{vOy} \\ =2\left(\widehat{uOy}+\widehat{vOy}\right)=2.\widehat{uOv} \end{gathered}$$.

Mà $\widehat{uOv}$ là góc vuông nên $\widehat{uOv}$ = 90^o.

Do đó, $\widehat{xOy}+\widehat{zOy}=2.\widehat{uOv}=2.90°=180°$ (1)

Mà $\widehat{xOy};\widehat{zOy}$ có cạnh chung là Oy (2)

Từ (1) và (2) suy ra $\widehat{xOy};\widehat{zOy}$ là hai góc kề bù.

Bài 3.32 trang 46 SBT Toán 7 Tập 1: Vẽ hình minh họa, ghi giả thiết, kết luận bằng kí hiệu và chứng minh định lí sau: Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng kia.

Lời giải:

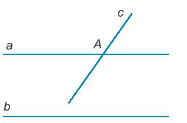
Giả thiết: a // b, c cắt a.

Kết luận: c cắt b.

Chứng minh: Giả sử c cắt a tại một điểm A. Nếu c không cắt b thì c song óng với b nên qua điểm A có hai đường thẳng a và c cùng song song với đường thẳng b do đó, theo tiên đề Euclid, c phải trùng với a. Nhưng theo giả thiết, c khác a vì c cắt a, vậy không thể có c không cắt b.